РАССЕЯНИЯ. МОДЕЛЬ КИРХГОФА.

АНАЛИЗ РАССЕЯННОГО БИОТКАНЬЮ ЛАЗЕРНОГО

ИЗЛУЧЕНИЯ В ПРИБЛИЖЕНИИ ОДНОКРАТНОГО

РАССЕЯНИЯ. МОДЕЛЬ КИРХГОФА.

Исследование характеристик рассеянного биотканью излучения несет важнейшую информацию о жизнедеятельности организма и возможных патологических изменениях. Главным является вопрос о достаточной точности и воспроизводимости измерений в соответствии с выбранной моделью исследуемой среды. Это заставляет предъявлять высокие требования к источнику зондирующего излучения с точки зрения монохроматичности и пространственной направленности, одновременно обеспечивая неразрушающее (т.е. достаточно слабое) воздействие. Общую схему разработки лазерного диагностического прибора, основанного на анализе рассеянного биотканью излучения можно представить в следующем виде:

1. Исходя из медицинских требований, устанавливаются типы лазерного источника и датчика рассеянного излучения (на уровне поисковых исследований это делается ориентировочно).

2. Выбирается статистическая модель рассеивающей среды и разрабатывается расчетная модель, позволяющая связать статистические характеристики среды с оптическими, допускающими измерение с помощью выбранных датчиков.

3. На основе разработанной теоретической модели проводятся экспериментальные исследования, имеющие целью опробование выбранной методики анализа рассеянного излучения на лабораторных моделях.

4. На основе проведенных теоретических и экспериментальных исследований определяются возможности методики в части выработки практических рекомендаций. Если эти рекомендации возможны, изготавливается экспериментальный (макетный) образец будущего диагностического прибора, допускающий испытания как in vitro (лабораторные), так in vivo (на животных). В случае успеха этих испытаний дальнейшая разработка ведется обычными способами.

Чтобы проиллюстрировать начальный этап (выбор и разработка расчетной модели, ориентированной на определенный тип лазерного источника и датчика рассеянного излучения), остановимся на низкоинтенсивных лазерах видимого или ближнего ИК диапазона, излучение которых будем считать заведомо не производящим изменений в исследуемой биосреде. В качестве датчика будем рассматривать волоконно-оптический датчик, работающий как регистратор излучения, рассеянного в обратную полусферу по отношению к падающему излучению.

Будем, как и ранее (Гл.25-28), работать в приближении скалярного квазимонохроматического волнового поля, но, в отличие от описания дифракции и пространственной фильтрации, среду будем считать случайно-неоднородной.

Уравнение Гельмгольца для такой среды имеет вид:

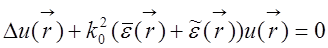(29.1)

где обозначено: 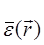- среднее по ансамблю реализаций значение диэлектрической проницаемости, 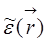- флуктуации диэлектрической проницаемости, дисперсию которых будем считать малой по сравнению со средним значением: 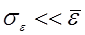. Имея в виду, что характерные изменения любых параметров биосреды происходят значительно медленнее, чем характерные времена изменения параметров падающего электромагнитного излучения, можно полагать случайность неоднородностей среды стационарной, т.е. применять там, где нужно, условие эргодичности. Ввиду условия малости флуктуаций, решение уравнения Гельмгольца будем искать в виде ряда по степеням малого параметра, связанного со случайным возмущением. Именно, пусть поле первичной волны 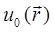удовлетворяет уравнению Гельмгольца в невозмущенной среде:

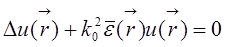
Рассматривая 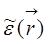как источник возмущающего уравнения Гельмгольца, найдем u( 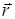) в представлении через функцию Грина:

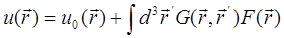
где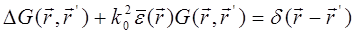

и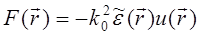

Тем самым имеем интегральное уравнение для возмущенного поля:

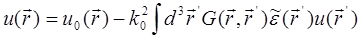( 29.2 )

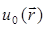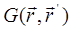В (29.2) подразумевается, что и удовлетворяют необходимым условиям на границе, а интегрирование распространяется на всю область, занятую неоднородностями 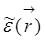. В качестве первого шага записывается поле в точке 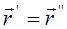и подставляется в правую часть ( 29.2). Повторяя операцию, получим ряд:

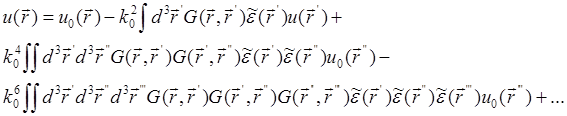( 29.3)

Разложение (29.3) носит название борновского разложения [ 1 ] и применяется в очень многих задачах, связанных с рассеянием.

Первый член ряда (29.3) 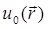представляет собой, как легко видеть, невозмущенное поле.

Второе слагаемое 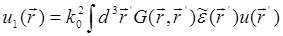представляет однократно рассеянное поле. Очевидно, 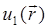линейно относительно возмущения .

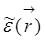По аналогии (n+1)-е слагаемое борновского ряда описывает n-кратно рассеянное поле, порожденное (n-1)-кратно рассеянной волной. Тем самым, ряд (29.3) можно рассматривать как разложение рассеянного поля 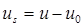по кратности рассеяния:

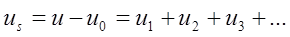( 29.4)

Здесь уже n-й член в правой части описывает n-кратное рассеяние и содержит n-кратный интеграл, под знаком которого фигурирует произведение 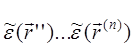. Таким образом, для суммирования ряда (29.4) необходимо вычисление моментов всех порядков и, кроме того, необходимо найти метод суммирования в каждом конкретном случае. Очевидно, каждый из этих конкретных случаев представляет собой достаточно сложную вычислительную задачу и требует ограничиться определенным порядком рассеянного поля.

Случай биосреды, характеризуется достаточно сильным поглощением излучения, и даже в области прозрачности биотканей (0,6…1,2 мкм) можно, как правило, ограничиться однократным рассеянием. Кроме того, неоднородности биосреды в большинстве задач можно считать крупномасштабными, т.е. 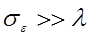. Имея в виду регистрацию с помощью волоконно-оптического датчика, требуется найти поле, рассеянное в обратную полусферу в пределах апертурного угла оптического волокна (не более 20˚). Это значит, что можно пренебречь затенениями одной неоднородности другой. Заметим, что для такой задачи непригодны большинство моделей объемного рассеяния (приближение геометрической оптики, приближение параболического уравнения, теория Ми и пр.), поскольку именно обратное рассеяние на крупномасштабных неоднородностях в этих моделях описывается неудовлетворительно.

Помогает модель Кирхгофа, работающая не в объеме, а на случайной поверхности, рассматриваемой как набор случайно наклоненных зеркал с коэффициентами отражения, рассчитанными по формулам Френеля. Среду в этом случае следует рассматривать как многослойную (совокупность таких случайных поверхностей, заполняющих бесконечное полупространство). Тем самым для расчета поля, рассеянного в обратную полусферу, следует решить две задачи: расчет интенсивности излучения, рассеянного одной поверхностью, затем построение итерационной модели, учитывающей вклад подстилающих слоев.

Рассмотрим вначале рассеяние от одной случайной поверхности. Пусть она задана уравнением 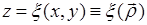. Ограничимся случаем в среднем плоской поверхности, т.е. примем 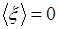. Без ограничения общности будем считать поперечный радиус корреляции неоднородностей поверхности 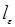вдвое большим, чем характерную «высоту неоднородностей» σ 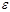(в данном случае их удобно называть неровностями). Пусть 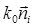- волновой вектор падающей волны, 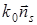- рассеянной (рис.29.1).

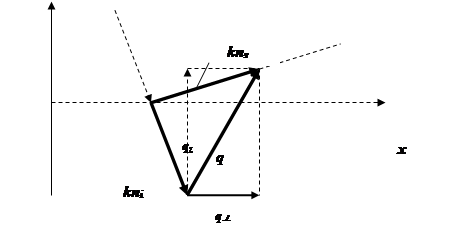Рис. 29.1.