Падение локально плоской квазимонохроматической волны

на случайную поверхность Кирхгофа

Тогда 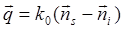- вектор рассеяния. Разложим 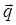на нормальную 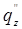и скользящую 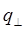компоненты. Падающую волну 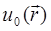можно считать локально плоской [ 1 ]:

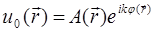( 29.5)

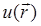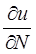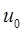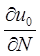а отраженное поле и его нормальную производную связать с и соотношениями:

(29.6)

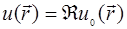
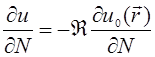
Условия (29.6) для локально плоской волны, падающей на плоскую поверхность, приближенно справедливы в соответствии с принципом Кирхгофа. Здесь 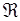– локальный амплитудный коэффициент отражения, вообще зависящий от угла падения излучения на случайную поверхность ξ и являющийся случайной величиной. Но в случае крупных и пологих неровностей можно принять 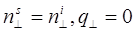и перейти в вычислении обратно рассеянного поля по формуле Грина (29.2) к интегрированию не по случайной , а по детерминированной поверхности 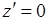(т.н. подстилающей [1]), что позволяет считать локальный коэффициент отражения 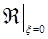, отвечающей зеркальному отражению 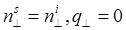, не случайной, а детерминированной величиной. Поскольку френелевские коэффициенты отражения в пределах углов до 20˚ меняются медленно [ 2 ], это приближение оправдано. Для средней интенсивности случайного поля:

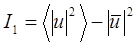(29.7)

имеем [ 1 ]:

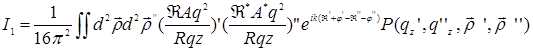(29.8)

Здесь R – расстояние от точки наблюдения 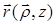до поверхности интегрирования, а штрихованные величины относятся к точкам подстилающей поверхности z = 0. В (29.8) появляется функция 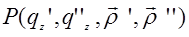, определяемая двумерной характеристической функцией 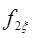с фурье-образом 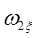и одномерным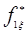и и :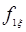

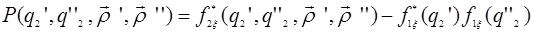(29.9)

Очевидно, Р=0 при 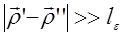(при этом 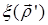и 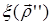становятся некоррелированными). Это позволяет разложить показатель экспоненты в (29.8) в ряд Тейлора по 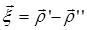с точностью до линейных членов, а перед экспонентой записать 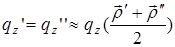. Тогда (29.8) превращается в следующее выражение:

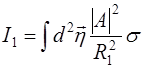(29.10)

где обозначено:

,

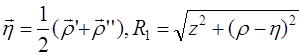а величина

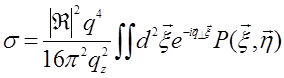(29.11)

имеет смысл дифференциального сечения рассеяния. В приближении крупных неоднородностей 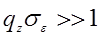основной вклад в (29.10) даст область малых ξ. Тогда:

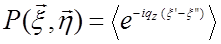(29.12)

Предположим, что неровности однородны, изотропны и распределены по нормальному закону (это предположение носит общий характер [1] ):

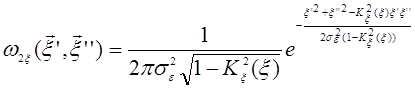(29.13)

Изотропность означает зависимость коэффициента корреляции 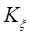только от модуля вектора 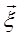. Тогда 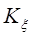в формуле (29.13) можно разложить в ряд Тейлора и пренебречь единицей по сравнению с экспонентой ( ).

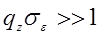Получим:

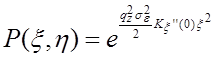(29.14)

Подстановка ( 29.14) в (29.11) дает:

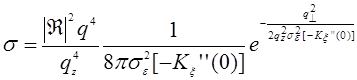(29.16)

Перейдем к характеристической функции случайных наклонов поверхности ξ, описываемых вектором:

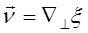(29.17)

Здесь 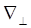- поперечный оператор Гамильтона.

Эта функция имеет максимум при 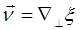=0 (наиболее вероятная ориентация элементов неровностей поверхности – параллельно подстилающей поверхности z = 0). Используя выражение для 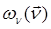[1]:

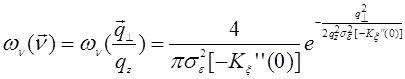(29.18)

Сравнивая (29.18) и (29.16), видим, что

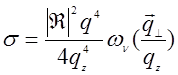
Вторая производная от коэффициента корреляции, входящая в (29.18) выражается через радиус корреляции 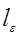[1]:

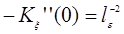
Тогда 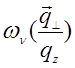принимает простой вид:

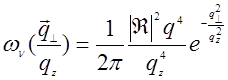
а дифференциальное сечение рассеяния:

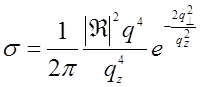
Выразим σ через угловые параметры, удобные для экспериментатора (см. рис.29.1). Если β – угол падения первичной волны на подстилающую поверхность, θ – угол между вектором рассеяния и нормально к той же плоскости, то , , .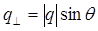

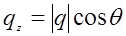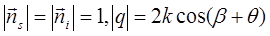Тогда имеем:

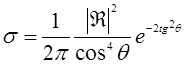(29.19)

Отличие функции 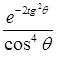от 1 в пределах угла θ<=20˚ не превышает 2,2%. Для интересующих нас случаев этим отличием можно пренебречь и считать:

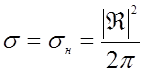(29.20)

Формула (29.20) возвращает нас из статистической радиофизики в классическую оптику: случайно распределенные на неровной поверхности зеркала аналогичны ламбертову диффузному отражению. Поставим в соответствие величине σ эффективный коэффициент отражения r_эфф . Для одной поверхности, как видно, r_эфф не зависит явно от параметров неровностей. Расчет r_эфф , учитывающий последовательное прохождение волной многих аналогичных поверхностей, требует записи френелевского коэффициента отражения в виде [2]

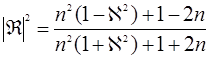(29.21)

Здесь n – действительная часть показателя преломления, 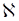- мнимая его часть, связанная с коэффициентом поглощения среды d соотношением [2]

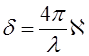(29.22)

Если рассматривать случайно отражающую поверхность Кирхгофа как совокупность плотно упакованных полусфер со средним радиусом 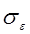, то пренебречь зависимостью локального амплитудного коэффициента отражения от угла падения на поверхность, вообще говоря, нельзя. Возможный алгоритм расчета может быть построен на модели «дисперсной среды», где шарики заменяются цилиндрами, а промежутки между цилиндрами считаются поглощающими. Если смотреть на поверхность нормально к подстилающей плоскости, то нетрудно определить долю промежутков :

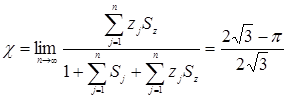(29.23)

В (29.23) обозначено:

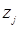- число промежутков в кольцевом «пояске», средний радиус которого равен j 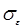(радиус каждого из кругов );

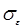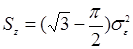- площадь одного промежутка;

S_j – площадь всех кругов в j – м кольцевом пояске.

Пользуясь для коэффициента отражения от одной поверхности Кирхгофа формулой (29.20) с учетом (29.23), построим процедуру вычисления общего коэффициента отражения от многослойной среды следующим образом:

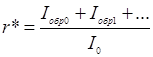(29.24)

В числителе (29.24) стоит ряд, каждый член которого строится следующим образом:

1. Согласно (29.20) и (29.23) находится коэффициент отражения верхней поверхности и определяется интенсивность принятого датчиком излучения .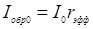

2. Вычисляется полное сечение рассеяния верхней поверхности в обратную полусферу.

3. Вычитая из I₀ полные потери излучения за счет отражения согласно п.2, найдем интенсивность прошедшего через эту поверхность внутрь излучения. При этом учтем поглощение в слое среды толщиной . Тем самым найдем интенсивность излучения, падающего на следующую поверхность Кирхгофа.

4. После вычисления падающей на следующую поверхность (согласно п.3) интенсивности I₁ вся процедура пп.1-2 повторяется. При этом определяется интенсивность излучения, отраженного следующей поверхностью.

5. Для нахождения I_обр1 найденная по п.4 интенсивность уменьшается за счет отражения на верхней поверхности с коэффициентом, найденным по п.1, за счет поглощения и за счет расходимости при прохождении расстояния от верхней поверхности до торца датчика (если торец датчика не примыкает непосредственно к поверхности).

6. Вычитая из I₀ полные потери (аналогично п.2) на обеих поверхностях, найдем интенсивность излучения, найдем интенсивность излучения, падающего на следующую отражающую поверхность, и т.д.

Повторяя аналогичную процедуру вычисления применительно к последующим слоям, прекратим процесс тогда, когда изменение r* за счет учета очередного слоя окажется меньше заданной точности вычисления. Для практических целей в большинстве случаев вполне достаточна точность порядка 1%, часто даже 10% (в биомедицинских измерениях, как правило, плохая воспроизводимость результатов и действует множество артефактов). Отметим, что только построение подобного вычислительного алгоритма дает возможность проследить зависимость коэффициента отражения от размера неровностей на поверхности Кирхгофа, поскольку однослойный коэффициент r_эфф от σ_ε явно не зависит. Конкретизация расчета упирается, тем самым, в предварительные измерения оптических характеристик биосреды (показателя преломления и коэффициента экстинкции), а также в морфологию, позволяющую хотя бы оценочно определить характерное расстояние между модельными слоями, принимаемое равным среднему масштабу неоднородности.

Литература к главе 29.

1. С.М. Рытов, Ю.А. Кравцов, В.И. Татарский. Введение в статистическую радиофизику. Часть II. Случайные поля. – М.: Наука, 1978, 464 с.

2. М. Борн, Э. Вольф. Основы оптики. – М. Наука, 1973, 720 с.