Симметричный конфокальный резонатор.

ОПТИЧЕСКИЕ РЕЗОНАТОРЫ СО СФЕРИЧЕСКИМИ

ЗЕРКАЛАМИ. ТЕОРИЯ ГАУССОВЫХ ПУЧКОВ

Симметричный конфокальный резонатор.

Итак, в работе Фокса и Ли [1] было показано, что, хотя в резонаторах типа Фабри-Перо возможны устойчивые конфигурации поля с учетом дифракционных потерь, распределение фазы собственных типов колебаний по плоской поверхности не соответствует форме этой поверхности. Авторы работы сделали естественный шаг: рассчитали аналогичным образом резонаторы со сферическими зеркалами, где фазовые искажения на вогнутой сферической поверхности оказались заметно меньше, чем на плоской. Поэтому среди выводов работы, наряду с заключением, что однородные плоские волны не являются нормальными модами открытых резонаторов, прозвучала рекомендация к использованию вогнутых зеркал сферической формы.

Кроме того, в пользу сферических зеркал говорят и чисто практические доводы, поскольку технология изготовления сферических поверхностей оптического качества хорошо отработана по сравнению с поверхностями другой формы кривизны. Отметим, однако, что и принципиальные соображения даже без утомительных численных расчетов обращают внимание именно на сферические зеркала. Во-первых, всякое отличие от плоской поверхности в первом приближении описывается проще всего именно как сфера. Во-вторых, вогнутое сферическое зеркало обладает фокусирующими свойствами и собирает внутрирезонаторный пучок «поближе» к оптической оси, тем самым снижая чувствительность резонатора к разъюстировкам.

Эти соображения, конечно, сами по себе достаточно примитивны, и ниже мы обоснуем выбор сферической формы зеркал с гораздо более фундаментальных позиций, но даже и здесь очевидно, что устойчивость резонатора, или критичность его к разъюстировкам, существенно зависит от выбора кривизны зеркал. Следовательно, для описания таких резонаторов к поперечным размерам зеркал и расстоянию между ними добавятся радиусы кривизны r₁иr₂(рисунок 6.1).

Рисунок 6.1. Резонатор со сферическими зеркалами.

После выхода в свет работы Фокса и Ли количество работ, посвященных оптическим резонаторам, стало лавинообразно нарастать. Так, в одной из первых публикаций Бойдом и Гордоном [2] было показано, что в случае симметричного конфокального резонатора (r₁ =r₂ = l) интегральное уравнение, описывающее поле в резонаторе, может быть решено аналитически. Распределение собственных типов колебаний по поверхности зеркал такого резонатора описывается сфероидальными функциями:

U_mn(ξ,η)=S_0m(2πN,ξ)S_0n(2πN, η),(6.1)

где ξ=х/a, η=y/a, N=a2/λl.

Поскольку собственные функции действительны, отражающие поверхности зеркал являются поверхностями постоянной фазы, то есть совпадают с волновым фронтом собственных типов колебаний.

Мнимая часть собственного значения равна

Im(lnγ_mn) = (kl+α_mn) = - (m+n+1)π/2+kl, (6.2)

т. е. фазовый сдвиг за один проход, вычитаемый из геометрического фазового сдвига, равен

α_mn = (m+n+1)π/2(6.3)

и не зависит от числа Френеля.

Собственные частоты резонатора определяются выражением

ν _mnq = c/4l(2q+1+m+n). (6.4)

Таким образом, спектр собственных частот симметричного конфокального резонатора сильно вырожден, а минимальный интервал частот между соседними модами равен с/4l.

Это, в частности, облегчает задачу реализации одночастотного режима работы лазера.

В наиболее распространенном случае больших чисел Френеля (2πN>>1) функции, описывающие поперечное распределение поля по поверхности зеркала вдоль каждой из координат, могут быть описаны в виде произведения функции Гаусса на полиномы Эрмита:

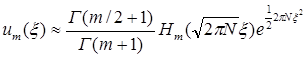(6.5).

Первые три полинома Эрмита записываются, как известно [3], в виде:

Н₀(х)=1; Н₁(х)=2х; Н₂(х)=2(х²-1). (6.6)

Так же, как в случае резонаторов с плоскими зеркалами, индекс в функции u_m показывает число нулей в распределении.

Следует отметить, что по мере удаления от оси резонатора наибольший вклад в распределение вносит экспонента функции Гаусса, описывающая сильное уменьшении амплитуды поля. Распределениеосновной моды(m = 0) просто описывается функцией Гаусса, без всяких полиномов Эрмита.

Таким образом, для собственных типов колебаний потери в конфокальном резонаторе оказываются меньше, чем в резонаторе с плоскими зеркалами таких же поперечных размеров. Зависимость потерь мощности за один проход от числа Френеля N для конфокального резонатора представлена на рисунке 6.2 [2].

Следует также отметить, что в симметричном конфокальном резонаторе создаются гораздо лучшие условия для селекции низшей моды, чем в резонаторе с плоскими зеркалами. Действительно, в районе N≈ 0,5 потери основной моды малы и существенно ниже потерь мод более высоких порядков.

Интересно, что в показатель экспоненты входит величина Nξ²=x²/Lλ, не зависящая от размеров зеркал. Поэтому при изменении поперечного размера зеркал величина освещенного пятна меняться не будет (не следует забывать, однако, что это справедливо при достаточно больших значениях числа Френеля).

Для основной моды радиус освещенного пятна на зеркале, соответствующий уменьшению амплитуды поля в е раз будет равен:

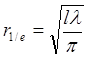. (6.7)

Соответственно диаметр пятна на зеркале, при котором мощность падает вдвое, равен:

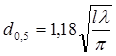. (6.8)

Если излучение основной моды выходит из резонатора через частично прозрачное зеркало, то диаграмма направленности может быть рассчитана из распределения поля на зеркале. Такой расчет приводит к следующему значению ширины диаграммы направленности по уровню половинной мощности:

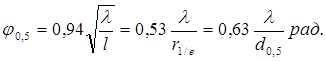(6.9).

Можно проследить за перемещением поверхности постоянной фазы в пространстве. При этом уравнение для синфазной поверхности, пересекающей ось резонатора в точке z₀, имеет вид

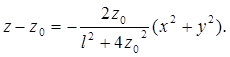(6.10)

В пределах принятого приближения это уравнение описывает сферическую поверхность с радиусом кривизны

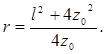(6.11)

При z₀ = ±l/2поверхности совпадают с поверхностями зеркал исходного резонатора. Видно, что синфазной является и фокальная плоскость зеркал

z ₀= 0.

В любой плоскости z = z₀ радиус пятна основной моды по уровню 1/e равен:

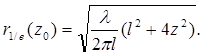(6.12)

Наименьший размер пятна получается в фокальной плоскости (перетяжка) и равен

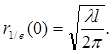(6.13)

Гауссовы пучки.

Расчет поля в оптических резонаторах был после Фокса и Ли проведен многими авторами для различных типов резонаторов. Устойчивые конфигурации мод, описываемые функциями различной сложности, отличались той общей закономерностью, что имели к краям зеркал обязательный спад амплитуды и интенсивности по Гауссу. Стремление получить аналитические выражения для распределения поля в резонаторе привело как зарубежных, так и отечественных авторов к формулам, дающим функции типа Фокса и Ли без расчета на ЭВМ.

В частности, практически одновременно с работой Бойда и Гордона, получивших аналитическое решение для круглых сферических зеркал, появилась серия работ Л.А. Вайнштейна [4], где в асимптотическом виде были получены все результаты, аналогичные Фоксу и Ли, без численных расчетов. С подачи Вайнштейна сформировалось целое новое направление в теоретической оптике — квазиоптика, позволившая представить все процессы, связанные с распространением лучей (т.е. геометро-оптические явления) с чисто волновой точки зрения.

Однако квазиоптика как таковая ушла в сторону от резонаторов, а в самой теории резонаторов ощущалась определенная концептуальная незавершенность. Именно, упорная «похожесть» устойчивых распределений поля в различных резонаторах в виде гауссовых «крыльев» при удалении от оптической оси заставила заподозрить наличие некоего общего принципа, позволяющего говорить не о формировании в пространстве распределения поля благодаря той или иной системе зеркал, а о существовании предельной конфигурации поля, которой та или иная система зеркал в большей или меньшей степени соответствуют. Впервые такая точка зрения на оптические резонаторы была разработана Когельником [5].

В этом понимании проблемы открытых резонаторов наличие идеальной конфигурации поля диктует конкретную систему зеркал, реализующую по возможности более близкий к идеальному пучок излучения. Ситуация, с одной стороны, напоминает центральную предельную теорему из теории вероятностей, с другой — квантовомеханическую задачу о минимизирующем соотношение неопределенностей волновом пакете.

На общие соображения относительно предельной конфигурации поля наталкивает даже простейший случай резонатора с плоскими зеркалами. Поле в таком резонаторе представляется в виде квазиплоской волны:

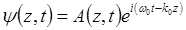
где 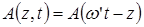. Отличие от плоской волны в том, что А ¹ const, почему и появляется приставка «квази».

Скорость, с которой перемещается максимум амплитуды (групповая скорость):

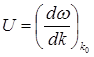при w = ck.

Представим амплитуду A(z,t) в виде интеграла:

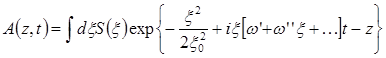(6.14)

и в случае квазиплоской волны ограничимся двумя членами разложения:

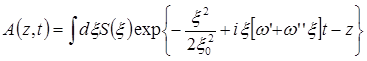(6.15)

Найдем интенсивность:

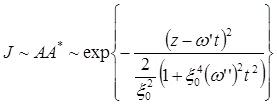(6.16)

т.е. к гауссовой форме J(x) приводит уже допущение о возможности обрыва ряда на втором члене. Но, вспоминая смысл соотношения неопределенностей, эта возможность означает, что волновой пакет по мере распространения расплывается минимально, т.е.: 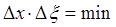(x — поперечная координата).

Применим теперь требование минимизации соотношения неопределенностей уже не к «чисто» квазиплоской волне, а к волновому пакету общего вида.

Пусть волновой пакет распространяется вдоль оси z, причем без ограничения общности (осесимметричный случай) можно полагать в поперечном направлении только одну координату x.

Рассмотрим сначала фиксированную точку z = 0 («остановленный» волновой пакет). Волновая функция 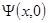, имеющая смысл комплексной амплитуды, может быть записана в виде интеграла Фурье:

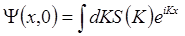(6.17)

с пространственным спектром:

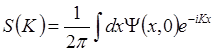(6.18)

Функции 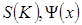(опустим пока зависимость от z) должны удовлетворять общим условиям сходимости интеграла Фурье, т.е. не имеют права не убывать на бесконечности, причем достаточно быстро. В соответствии с принципами функционального анализа можно записать:

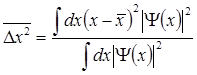(6.19)

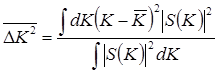(6.20)

Упростим выражения (6.19) и (6.20). Выбором системы координат всегда можно сделать 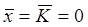, а знаменатели обоих выражений (6.19) и (6.20) представляют собой условия нормировки как волновой функции, так и ее спектра:

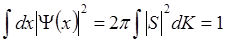(6.21)

Запишем поэтому (6.19) и (6.20) в виде:

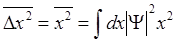(6.22)

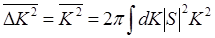(6.23)

Перейдем в (6.22) к интегрированию по К. Это можно сделать с помощью формулы:

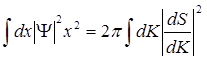(6.24),

следующей из (6.17) и (6.18).

Используя (6.24), запишем:

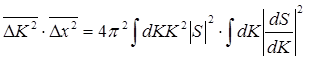(6.25)

Любые две функции в пространстве волновых функций подчиняются неравенству Коши:

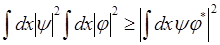(6.26)

причем равенство достигается только при пропорциональности функций y и j или их линейной зависимости как векторов функционального пространства. Это значит, что (6.25) можно переписать в виде:

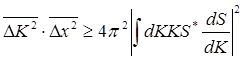(6.27)

Неравенство (6.27) превращается в равенство, т.е. 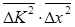минимизируется, при условии:

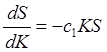(6.28)

т.е. пропорциональности подынтегральных функций. В (6.28) знак "–" поставлен в силу того, что функция S(K) не имеет права возрастать на бесконечности. Само условие (6.28) представляет собой, как видно, дифференциальное уравнение, дающее как возрастающую (не имеющую физического смысла), так и убывающую экспоненты. Для S, тем самым, имеем:

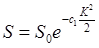(6.29)

и соответственно:

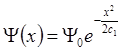(6.30)

Константа с₁ характеризует ширину получившихся гауссовых функций, а S₀ и Y₀ легко найти из условия нормировки.

Итак, волновая функция, обеспечивающая минимум соотношению неопределенностей, является гауссовой, а распределение поля в пространстве, описываемое такой функцией, естественно назвать гауссовым пучком. Для уточнения смысла с₁ оценим произведение 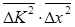численно. Интеграл

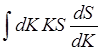
можно взять по частям, в результате получим:

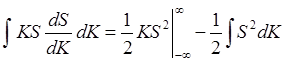(6.31)

Проинтегрированная часть, очевидно, обращается в 0, поскольку S²(K) на бесконечности убывает быстрее, чем K, а оставшийся интеграл в (5.31) представляет собой условие нормировки для S(K). Поэтому:

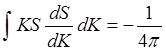(6.32)

и

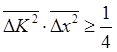(6.33)

При условии равенства (5.33) дает:

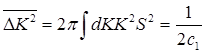(6.34)

Обозначим:

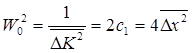(6.35)

Как видно, W₀ , определяемая константой с₁, имеет вполне реальный смысл (рисунок 6.3): 2W₀ — ширина функции Y₀(x) на уровне 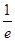. Эта величина является существенной характеристикой волнового пакета.

Если теперь разрешить волне распространяться (отказаться от условия z = 0), то волновая функция примет вид:

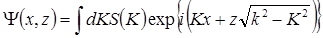(6.36)

где 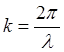— волновое число.

Полагая, что расходимость пучка мала, запишем:

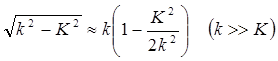(6.37)

Тогда Y(x, z) преобразуется к виду:

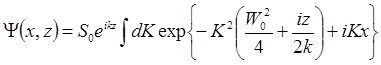(6.38)

Интеграл в (6.38) вычисляется аналитически. После интегрирования получаем:

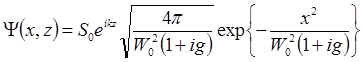(6.39)

В (6.39) введена величина:

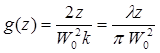(6.40)

называемая волновым параметром пучка.

Представим Y(x, z) в виде квазиплоской волны, т.е. выделим амплитудный и фазовый множители 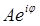. При этом избавимся от комплексных величин в знаменателе. Получим:

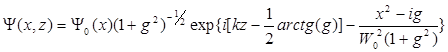(6.41)

Хотя формула (6.41) представляется несколько тяжеловесной, все ее члены имеют ясный физический смысл. Именно, множитель при экспоненте характеризует изменение амплитуды вдоль оси z. В показателе экспоненты выделяется мнимый член, где 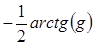дает поправку к регулярному набегу фазы за счет того, что волна не плоская. В отличие от неограниченно возрастающего kz, поправка ограничена: 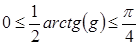, поэтому при очень больших z волна все более должна походить на плоскую. Однако в каждой конкретной точке рассматривать ее как плоскую нельзя. Это полностью соответствует выводам Фокса и Ли и других исследователей полей в резонаторах, хотя мы еще ни словом не упомянули о зеркалах. Действительный член в показателе экспоненты характеризует зависимость ширины волнового пакета в зависимости от z:

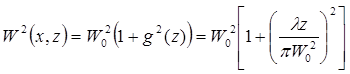(6.42)

Как видно, введенный волновой параметр g(z) характеризует «расплывание» волнового пакета по мере его распространения. Если g >>1, то наблюдается рост W(x,z) по закону, близкому к линейному, т.е. зависимость W(x,z) имеет асимптоту, наклоненную под углом 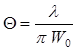к оси z:

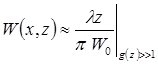(6.43)

Величина 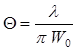называется асимптотическим углом расходимости пучка.

Последний член в показателе экспоненты характеризует изменение фазы при изменении поперечной координаты:

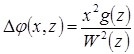(6.44)

Вблизи оси можно рассматривать волновой фронт как сферический. Найдем радиус кривизны фронта, считая задачу осесимметричной (рисунок 6.4):

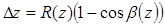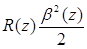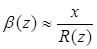Основной набег для малых b(z) равен . Но , тогда 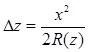. Соответственно набег фазы:

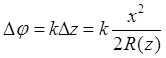
С другой стороны, согласно (5.44):

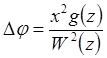
Приравнивая выражения для Dj, получим:

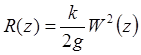(6.45)

Из (6.45) следует, что существует z, при котором фронт имеет максимальную кривизну. В самом деле, переписав (6.45) в виде:

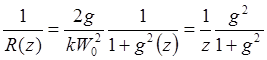(6.46)

видим, что при малых z кривизна неограниченно убывает, обращаясь в 0 при z = 0, а при больших z она стремится к 0 асимптотически.

Дифференцируя (6.46), найдем

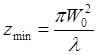(6.47)

и

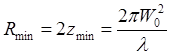(6.48)

Фундаментальность гауссова пучка как предельной устойчивой конфигурации поля, «диктующей» выбор конкретной геометрии резонатора, ставит на свои места все формулы типа (6.4) — (6.13), в которых теперь просматривается глубокая логическая взаимосвязь, ускользающая при отсутствии вывода гауссовости пучка из самых общих соображений.

В самом деле, основная мода резонатора с этой точки зрения является не просто собственной функцией с наинизшим номером, а наиболее устойчивым пространственным распределением поля, доставляющим минимум соотношению неопределенностей. Поэтому нет необходимости проверять ее на минимум потерь ― коль скоро она реализуется, остальные типы колебаний могут «отдыхать». В случае же искусственного создания невыгодных для основной моды условий («неправильная» геометрия резонатора) могут возбуждаться моды более высоких порядков, которые можно рассматривать как «возбужденные состояния» внутрирезонаторного квазигармонического осциллятора. И здесь, конечно возникает полный простор для вычисления полиномов Эрмита, Лагерра и т.п., но теперь при этом нет ощущения хаоса, поскольку обращение к таблицам специальных функций полностью выдержано логически. Обратный же ход рассуждений (от собственных функций к Гауссу) неминуемо приводит к рассмотрению гауссовых пучков как некоего частного случая и тем самым нарушает всю стройность и гармонию в поведении устойчивых типов колебаний.

При выводе гауссова пучка из соотношения неопределенностей как инварианта, обеспечивающего минимум этого соотношения, необходимо уточнение пути нахождения конкретной величины перетяжки W_{0 .} Наиболее простым является путь задания желаемой асимптотической расходимости пучка при заданной длине волны излучения. Заметим, что при изменении структуры пространственного спектра волнового пакета (аналогично нарушению состояния «свободного движения» волнового пакета в квантовой механике [6]) возможно изменение значения нижней границы для соотношения неопределенностей. Соответственно изменятся и параметры гауссова пучка, но сама гауссовость сохранится как атрибут устойчивой пространственной конфигурации поля.