Использование матричных методов при расчете характеристик

Гауссовых пучков.

В предыдущих разделах мы установили, что в резонаторах устойчивой конфигурации основная мода (наиболее интересная с точки зрения практических применений) имеет гауссово поперечное распределение, а зеркала резонатора являются синфазными ей поверхностями. Это позволяет использовать простую и эффективную матричную методику для расчета прохождения излучения через оптические системы и исследования характеристик оптических резонаторов [7].

Для начала обратимся к распространению параксиальных пучков лучей, широко используемых в рамках геометрической оптики. Напомним, что параксиальными называются лучи, для которых положение точки в пространстве изображений не зависит от угла, образуемого производящим лучом с оптической осью. Распространение параксиальных лучей через линейную оптическую систему описывается матрицей передачи. Любой луч может быть однозначно задан двумя параметрами в точке его прохождения — расстоянием от оси резонатора z и углом наклона к ней (рисунок 6.5).

Если луч распространяется в среде с показателем преломления n, то можно записать V = n sin α ≈ n α.

Прохождение лучей через пассивную оптическую систему (рис.6.5) описывается линейным преобразованием:

=

или

y₂ = A y₁ + BV₁ y₂ A B y₁

V₂ = C y₁ + DV₁ V₂ C D V₁

При этом матрица оказывается унимодулярной: AD – BC = 1. Элементы матрицы связаны с фокусным расстоянием системы и координатами ее главных плоскостей соотношениями:

F = -1/C; h₁= (D – 1)/C; h₂ = (A – 1)/C (6.50)

 

В таблице 6.1 приведены матрицы передачи для четырех простейших оптических систем: плоский промежуток, слой, тонкая линза, слой с линзой и распределенная линза, образованная слоем среды с квадратичным распределением показателя преломления.

 

Таблица 6.1

	Оптическая схема	Матрица передачи
		1 d   -1/f 1-d/f
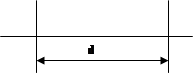
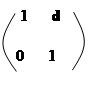
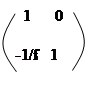
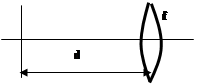
	n=1 n=n0-0,5n2r2 d	cos d 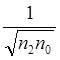s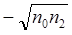in d sin d cos d

 

Если лучи проходят последовательно несколько оптических систем, то результирующая матрица передачи вычисляется как произведение соответствующих матриц. Так, матрица для оптической системы 3 является произведением двух первых.

При этом оказывается, что с помощью АВCD-матриц можно описывать преобразование гауссовых пучков при прохождении через оптическую систему. Используя комплексный параметр

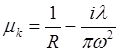, (6.51)

где R – радиус кривизны волнового фронта, а ω ― радиус, описывающий гауссов пучок в k-ой плоскости, можем описать его трансформацию оптической системой, расположенной между двумя плоскостями и характеризующейся матрицей АВСD, формулой

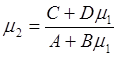. (6.52)

Если применить матричный метод к устойчивому резонатору, основная мода которого является гауссовым пучком, то после полного обхода резонатора комплексный параметр для гауссова пучка, описывающего основную моду резонатора, должен совпасть с исходным. Расписывая отдельно равенства для действительной и мнимой частей, получаем уравнения для параметров, описывающих низший собственный тип колебаний (основную моду) резонатора и получить выражение значения радиуса ω₀ основной моды устойчивого резонатора , которое может быть записано в виде:

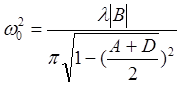. (6.53)

Литература к лекции 6.

1. Fox A.H., Lee T. //Bell Syst. Tech. Journal, 1961, 40, 453. Имеется перевод в сборнике статей «Лазеры», пер. с англ. под ред. М.А. Жаботинского и Т.А. Шмаонова. ― М.: ИЛ., 1963.

2. Бойд Дж., Гордон Дж. Конфокальный резонатор со многими типами колебаний. В сб. статей «Лазеры», пер. с англ. под ред. М.Е. Жаботинского и Т.А. Шмаонова, ― М.: ИЛ., 1963.

3. Карлов Н.В. Лекции по квантовой электронике. ― М.: Наука, 1983.

4. Вайнштейн Л.А. Открытые резонаторы и открытые волноводы. — М.: Сов. радио, 1966, 475 с.

5. Kogelnik H., Lee T. Laser beams and resonators. // Proc. IEEE, 1966, 54, 1312. — Имеется перевод: Когельник, Ли. Резонаторы и световые пучки лазеров. ТИИЭР, 1966, 54, № 10, 95.

6. Давыдов А.С. Квантовая механика. ― М.: Наука, 1973.

7. Джерард А., Бёрч Дж. М. Введение в матричную оптику. — М.: Мир, 1978, с. 130 – 147.