Деформации и напряжения. Упругие коэффициенты.

<21 22 232425 26 27 >

Деформации объема удобно рассмотреть на примере модели линейного элемента(ребро параллелепипеда), то есть тела, имеющего только один размер. Физически такое тело можно представить в виде длинного и узкого стержня, поперечный размер которого пренебрежимо мал в сравнении с длиной. Закрепим такой стержень верхним торцом, а к противоположному концу приложим растягивающую нагрузку (силу) - F (рис 36).

В результате приложения этой силы частички сместятся. Обозначим вектор смещения через 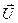, а его составляющие по осям координат через u, v и ω соответственно. В рассматриваемом случае можно учитывать только составляющую u, пренебрегая остальными. Обозначим смещение, полученное частичками, отстоящими от закрепленного конца стержня на расстояние х через u. Вследствие действия сил сцепления между частичками, составляющими стержень (сил межчастичного взаимодействия, пружинок),– смещения будут тем меньше, чем ближе к закрепленному концу стержня они находятся. Это значит, что более удаленные частички, то есть х + Δх получат большее смещение, то есть u +Δu.

Возьмем теперь разность смещений и отнесем ее к разности удалений х 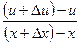. Если устремить Δх к нулю и взять предел этого отношения, то перейдем от бесконечно малых к производной .

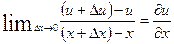По физическому смыслу это есть относительное удлинение линейного элемента, его деформация, которую мы обозначим как e_xx. Теперь возьмем векторную сумму 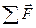всех сил, действующих на свободный торец стержня и отнесем ее к площади его поперечного сечения S –получим величину приложенного напряжения, которое обозначим через Р

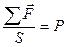
Составляющая этого вектора Р_xбудет связана с деформацией e_xx линейной зависимостью, называемой законом Гука: величина деформации прямо пропорциональна величине приложенного напряжения ( вскользь этот закон уже упоминался в разделе гравиразведка). Этому закону подчиняются упругие среды. Понятно, что геологические среды поведут себя как упругие только тогда, когда напряжения будут невелики и весьма кратковременны (как известно, геологические среды при длительно прилагаемых нагрузках деформируются пластически, «текут», изгибаются в складки без разрыва сплошности, а если напряжения велики, то с разрывом – сбросы, надвиги).

Закон Гука может быть записан в виде соотношения

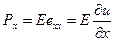, отсюда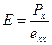

Коэффициент пропорциональности между напряжением и деформацией обозначим через Е. Этот упругий коэффициент носит название модуль Юнга или коэффициент продольного растяжения.

По физическому смыслу Е – это сила, которую надо приложить, чтобы произошло удлинение, равное единице длины, то есть одному метру. Размерность Е, как это видно из приведенного соотношения, совпадает с размерностью напряжения Р, поскольку e_xx – относительная (безразмерная) величина. То есть размерность Е - 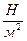(ньютон на метр в квадрате). Вполне понятно, поскольку растянуть линейный элемент на метр исключительно тяжело, что сами по себе величины Е очень велики. Так, для осадочных пород значения Е заключены в диапазон от 0,05·10¹⁰ до 10·10¹⁰н/м², для кристаллических диапазон у'же и сами значения выше - от 3·10¹⁰до 20·10¹⁰н/м², для воды 2·10¹⁰н/м².

Еще один упругий коэффициент, смысл которого может быть уяснен из приведенной модели, носит название коэффициента поперечного сжатия, или коэффициента Пуассона, обозначаемого греческой буквой ν(ню). Он представляет собой отношение относительного сжатия стержня δy/y к относительному удлинению δx/x

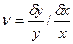
Понятно, что в результате приложения растягивающей нагрузки стержень удлинится на δх (по отношению к первоначальной длине х) и станет уже на δy (по отношению к первоначальной длине y).

Понятно также, что ν – безразмерная величина и, как правило, очень маленькая. Для подавляющего большинства горных пород ν близко к 0,25 и только для очень рыхлых пород ВЧР (верхней части разреза) приближается к 1.

Через линейные элементы (точнее, через относительные удлинения всех сторон объемного тела – параллелепипеда, который легко описать тремя линейными элементами, исходящими из одной точки – вершины: длина х, ширина у, высота z) может быть найдено изменение всего этого малого объема, его объемное расширение, или кубическая дилатация Θ

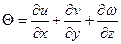
Из приведенной записи хорошо видно, что это математическая операция с вектором смещения 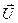. Такая операция называется дивергенцией вектора и индексируется оператором div, что означает расхождение

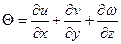= div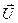

Модель сдвиговой деформации представлена на рис.37 на примере одной из граней рассматриваемого параллелепипеда, одна сторона которой закреплена, а к противоположной приложена внешняя сила F.

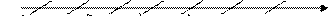
Рис.37. Сдвиговая деформация.

Тогда понятно, что частички из ряда, удаленного от начала координат на расстояние х получит смещение v (составляющая вектора 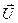вдоль оси y, по направлению которой приложена сила F), а частички х+Δх сместятся сильнее – v+Δv. Взяв, подобно тому, как это было сделано выше, предел отношения приращения по у к приращению по х при Δх , стремящемуся к 0, получим выражение для деформации γ₁в виде производной

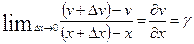
Сама эта деформация выразится в сдвиге сторон или в скошении γ прямого угла , точнее, она будет представлять собой тангенс этого угла, но для малых углов, как известно tgγ ≈ γ . Если закрепить другую грань (по оси х) и приложить в направлении х внешнюю нагрузку к противоположной грани, то получим аналогичное скошение 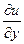. Суммарное скошение определяется как 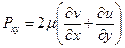, где Р_ху – составляющая тангенцильного напряжения, а μ – коэффициент пропорциональности между напряжением и деформацией, называемой модулем сдвига. Таким образом, видно, что при касательных напряжениях происходит изменение формы первоначальных объемов – деформация формы (или сдвига частичек одного ряда относительно другого).

Через упругие коэффициенты записываются выражения для скорости продольных и поперечных волн

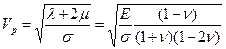
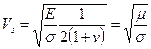
Здесь σ – плотность среды, а λ – один из упругих коэффициентов Ламе (λ и μ). не имеющий физического смысла. Из этих формул хорошо видно, что V_p>V_s. Теоретические исследования, подтверждаемые практикой , показывают, что .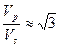

Теперь можно подытожить основные отличия объемных волн P и S: разные скорости, разный характер поляризации колебаний и, наконец, вполне понятно, что поперечные волны могут распространяться только в твердых средах (деформации формы!), а продольные в любых. Помимо объемных волн существуют еще поверхностные.

Поверхностные волны обычно возникают при возбуждении колебаний вблизи дневной поверхности, а распространяются не вглубь среды, а бегут вдоль этой поверхности в подстилающем слое, толщина которого равна примерно длине волны. Поверхностные волны в основном низкочастотные с весьма своеобразным продольно-поперечным характером поляризации колебаний: частицы в этой волне движутся по эллиптическим орбитам. Скорости распространения этих волн наиболее низкие: V_R≈0,9V_s

Такие волны называют Релеевскими(R), по имени знаменитого британского физика лорда Релея, который дал первое теоретическое их описание. Релеевские волны всегда в той или иной мере присутствуют на сейсмических записях, являясь сильной помехой для регистрации отраженных волн.

Помимо Релеевских существуют еще поверхностные волны Лява с чисто поперечным характером поляризации колебаний. Они обычно возникают при глубокофокусных землетрясениях и на сейсморазведочных записях не наблюдаются.

<21 22 232425 26 27 >

Дата добавления: 2017-01-26; просмотров: 2763;