Изгибаемые элементы
Центрально-растянутые и центрально-сжатые элементы
Задача 1.1.1
Определить наименьший размер сечения «b» при следующих условиях: N = 134,4 кН, диаметр отверстий d = 2 см, древесина лиственница I сорта, условия эксплуатации – 2-й класс, режим нагружения В.
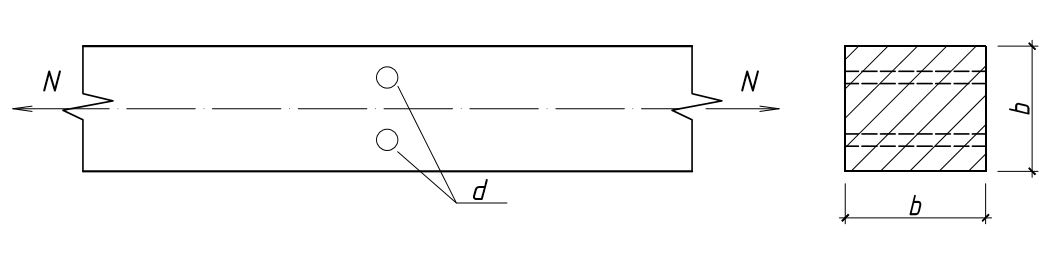
Рис. 1.1
Решение:
Расчет центрально-растянутого элемента производится по формуле
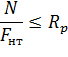
где 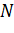 – расчетная продольная сила,
– расчетная продольная сила,
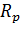 – расчетное сопротивление древесины растяжению вдоль волокон,
– расчетное сопротивление древесины растяжению вдоль волокон,
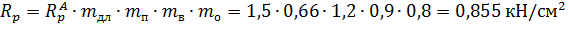
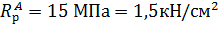 – расчетное сопротивление растяжению вдоль волокон для элемента из цельной древесины (табл. 3, [4]);
– расчетное сопротивление растяжению вдоль волокон для элемента из цельной древесины (табл. 3, [4]);
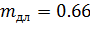 – коэффициент длительной прочности (табл. 4, [4]);
– коэффициент длительной прочности (табл. 4, [4]);
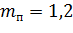 – коэф., учитывающий породу древесины (табл. 5, [4]);
– коэф., учитывающий породу древесины (табл. 5, [4]);
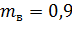 – коэф., учитывающий условия эксплуатации (табл. 9, [4]);
– коэф., учитывающий условия эксплуатации (табл. 9, [4]);
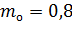 – коэф., учитывающий наличие ослабления (п. 6.9 г [4]).
– коэф., учитывающий наличие ослабления (п. 6.9 г [4]).
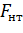 – площадь поперечного сечения элемента нетто.
– площадь поперечного сечения элемента нетто.
С учетом ослабления площадь сечения выразим следующим образом
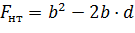
Подставив все известные значения в исходную формулу, получим требуемый размер поперечного сечения « 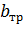 »
»
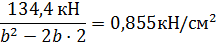
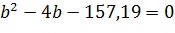
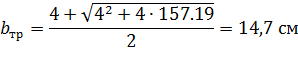
Наименьшая длина стороны квадратного сечения равна 14,7 см
Задача 1.1.2
Определить несущую способность растянутого элемента при следующих условиях: сечение 25(h) x 12,5(b) см, расстояние между отверстиями а = 12 см, глубина выреза с = 2,5 см, диаметр отверстия d = 2 см, древесина – клен II сорта, режим нагружения В.
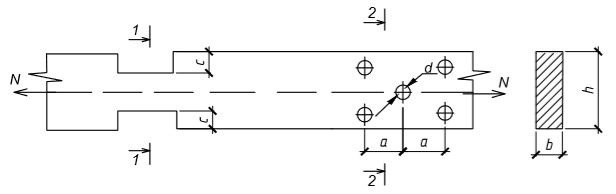
Рис. 1.2
Решение:
Определяем какое из мест с ослаблениями является более опасным.
Площадь сечения нетто по разрезу 1-1:
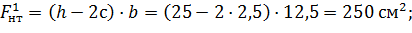
Площадь сечения нетто по разрезу 2-2:
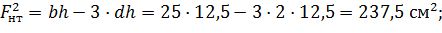
т.к. отверстия на расстоянии меньше 200 мм, то их следует объединить в одно сечение (согласно п. 7.1 [4]).
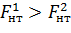 – более слабым является сечение 2-2.
– более слабым является сечение 2-2.
Найдем максимальную допустимую нагрузку, пользуясь формулой (ф. 10, [4]):
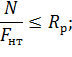
отсюда
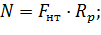
где:
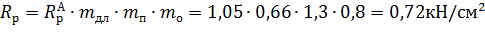
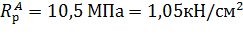 – расчетное сопротивление растяжению вдоль волокон для элемента из цельной древесины (табл. 3, [4]);
– расчетное сопротивление растяжению вдоль волокон для элемента из цельной древесины (табл. 3, [4]);
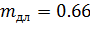 – коэффициент длительной прочности (табл. 4, [4]);
– коэффициент длительной прочности (табл. 4, [4]);
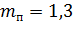 – коэф., учитывающий породу древесины (табл. 5, [4]);
– коэф., учитывающий породу древесины (табл. 5, [4]);
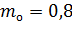 – коэф., учитывающий наличие ослабления (п. 6.9 г [4]).
– коэф., учитывающий наличие ослабления (п. 6.9 г [4]).
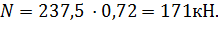
Максимальная несущая способность элемента 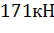 .
.
Задача 1.1.3
Подобрать размеры поперечного сечения сжатой шарнирно закрепленной стойки квадратного сечения при следующих условиях: длина l = 400 см, усилие N = 60 кН, древесина лиственницы II сорта, условия эксплуатации 3-го класса, режим нагружения В.
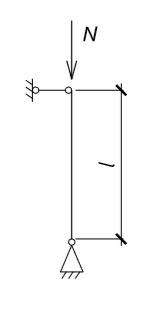
Рис. 1.3
Решение:
Расчет центрально сжатого элемента на устойчивость с учетом условий задачи следует производить по следующей формуле (ф. 12 [4]):
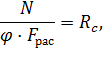
где
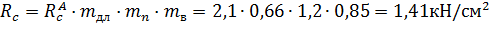
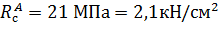 – расчетное сопротивление сжатию вдоль волокон для элемента прямоугольного сечения (табл. 3, [4]);
– расчетное сопротивление сжатию вдоль волокон для элемента прямоугольного сечения (табл. 3, [4]);
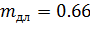 – коэффициент длительной прочности (табл. 4, [4]);
– коэффициент длительной прочности (табл. 4, [4]);
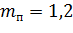 – коэф., учитывающий породу древесины (табл. 5, [4]);
– коэф., учитывающий породу древесины (табл. 5, [4]);
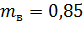 – коэф., учитывающий условия эксплуатации (табл. 9, [4]);
– коэф., учитывающий условия эксплуатации (табл. 9, [4]);
Примем, что гибкость 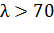 , тогда коэффициент продольного изгиба:
, тогда коэффициент продольного изгиба:
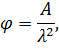
где
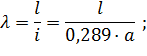
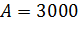 – для цельной древесины,
– для цельной древесины,
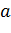 – длина стороны сечения.
– длина стороны сечения.
Подставляя найденные значения в первоначальную формулу, получим:
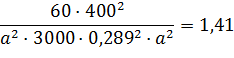

По сортаменту [5] принимаем сечение 150 х 150 мм.
Проверяем правильность выбранной формулы для определения коэффициента устойчивости.
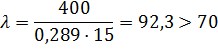
Задача 1.1.4
Определить несущую способность центрально-сжатого стержня при следующих условиях: расчетная длина в обоих плоскостях l = 5 м, сечение – 250(h) x 150(b) мм, диаметр отверстия d = 24 мм, древесина – береза II сорта, условия эксплуатации – 2-й класс, режим нагружения В.
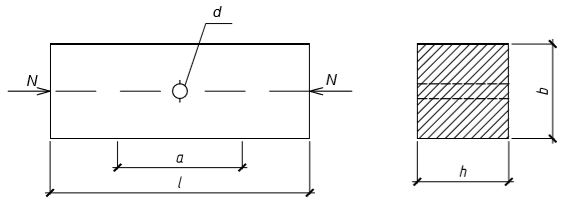
Рис. 1.4
Решение:
Несущая способность центрально-сжатого стержня при данных условиях определяется из расчета на устойчивость по следующей формуле (ф. 12 [4]):
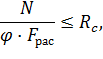
где 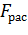 – расчетная площадь поперечного сечения зависит от наличия и расположения ослаблений сечения (п. 7.2 б [4]).
– расчетная площадь поперечного сечения зависит от наличия и расположения ослаблений сечения (п. 7.2 б [4]).
Потеря устойчивости происходит в плоскости с меньшей жесткостью, поэтому:
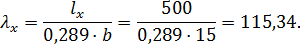
Так как гибкость 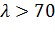 , то коэффициент
, то коэффициент 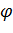 находим по следующей формуле:
находим по следующей формуле:
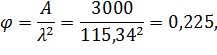
где 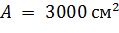 – для цельной древесины.
– для цельной древесины.
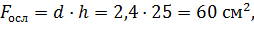 что составляет
что составляет 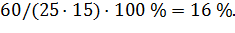
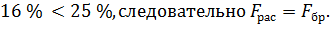
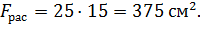
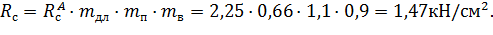
где:
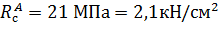 – расчетное сопротивление сжатию вдоль волокон для элемента прямоугольного сечения (табл. 3, [4]);
– расчетное сопротивление сжатию вдоль волокон для элемента прямоугольного сечения (табл. 3, [4]);
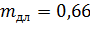 – коэффициент длительной прочности (табл. 4, [4]);
– коэффициент длительной прочности (табл. 4, [4]);
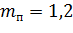 – коэф., учитывающий породу древесины (табл. 5, [4]);
– коэф., учитывающий породу древесины (табл. 5, [4]);
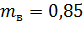 – коэф., учитывающий условия эксплуатации (табл. 9, [4]);
– коэф., учитывающий условия эксплуатации (табл. 9, [4]);
Подставив все известные значения в исходную формулу и заменив неравенство знаком равно, выражаем нужное значение.
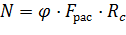
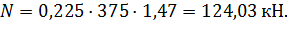
Максимальная несущая способность элемента 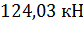 .
.
Изгибаемые элементы
Задача 1.2.1
Найти минимальное сечение балки, удовлетворяющее требованиям прочности, при показанной ниже расчетной схеме и при следующих условиях: нагрузки Р = 4 кН, длина консоли 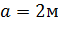 , древесина лиственница II сорта, условия эксплуатации – 2-й класс, режим нагружения В. Сечение принять прямоугольное с условием, что h = 1,5b.
, древесина лиственница II сорта, условия эксплуатации – 2-й класс, режим нагружения В. Сечение принять прямоугольное с условием, что h = 1,5b.
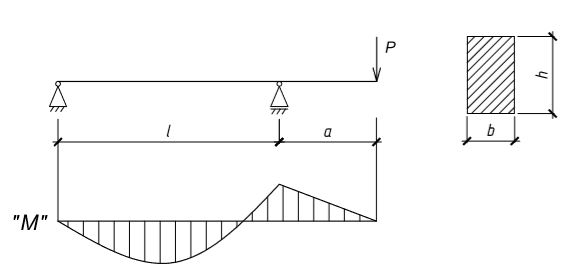
Рис. 1.5
Решение:
Расчет изгибаемых элементов на прочность по нормальным напряжениям в данных условиях следует выполнять по формуле (ф. 23 [4]):
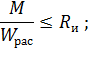
Максимальный изгибающий момент при такой расчетной схеме будет возникать над правой опорой. Определим значение момента рассматривая консольный участок:
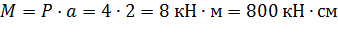
Момент сопротивления прямоугольного сечения находим по формуле:
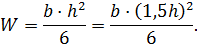
Расчетное сопротивление изгибу
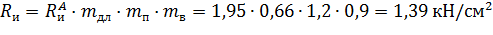
где
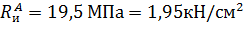 – расчетное сопротивление изгибу вдоль волокон для элемента прямоугольного сечения (табл. 3, [4]);
– расчетное сопротивление изгибу вдоль волокон для элемента прямоугольного сечения (табл. 3, [4]);
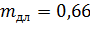 – коэффициент длительной прочности (табл. 4, [4]);
– коэффициент длительной прочности (табл. 4, [4]);
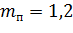 – коэф., учитывающий породу древесины (табл. 5, [4]);
– коэф., учитывающий породу древесины (табл. 5, [4]);
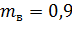 – коэф., учитывающий условия эксплуатации (табл. 9, [4]);
– коэф., учитывающий условия эксплуатации (табл. 9, [4]);
Подставляя все известные значения в первоначальную формулу найдем минимальное значение размера «b».
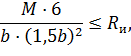
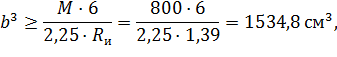
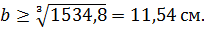
Так как полученная ширина сечения находится в пределах 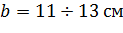 , то согласно таблице 3 [4] расчетное значение
, то согласно таблице 3 [4] расчетное значение 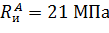 , поэтому расчет следует уточнить.
, поэтому расчет следует уточнить.
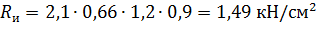
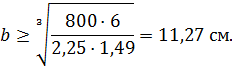
Минимальное сечение 11,27(b) x 16,91(h).
Задача 1.2.2
Проверить прочность балки по нормальным напряжениям при следующих условиях: пролет l = 4 м, нагрузка q = 3 кН/м, сечение – 120(b) x 200(h) мм, угол поворота сечения 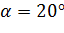 древесина сосна II сорта, условия эксплуатации – 3-й класс, режим нагружения В.
древесина сосна II сорта, условия эксплуатации – 3-й класс, режим нагружения В.
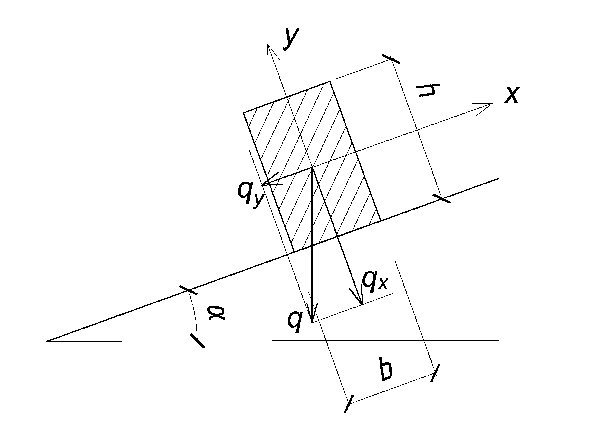
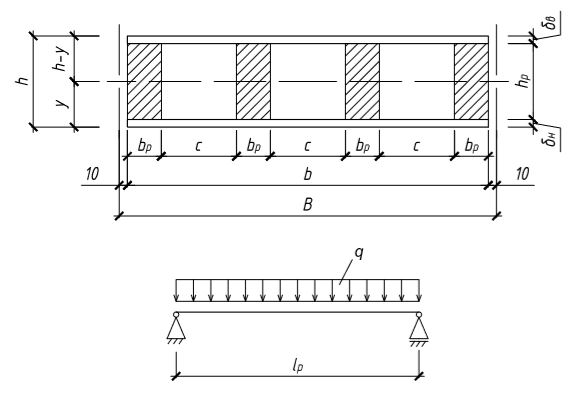
Рис. 1.6
Решение:
В случае, когда плоскость нагружения не совпадает ни с одной из главных осей сечения, элемент находится в состоянии косого изгиба. Для элементов цельного сечения расчет выполняется по следующей формуле (ф. 26 [4]).
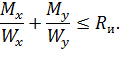
где
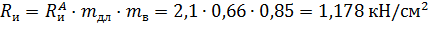
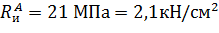 – расчетное сопротивление изгибу вдоль волокон для элемента прямоугольного сечения (табл. 3, [4]);
– расчетное сопротивление изгибу вдоль волокон для элемента прямоугольного сечения (табл. 3, [4]);
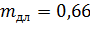 – коэффициент длительной прочности (табл. 4, [4]);
– коэффициент длительной прочности (табл. 4, [4]);
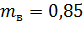 – коэф., учитывающий условия эксплуатации (табл. 9, [4]);
– коэф., учитывающий условия эксплуатации (табл. 9, [4]);
Раскладываем нагрузку на составляющие, действующие по направлению главных осей сечения:
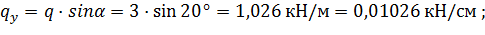
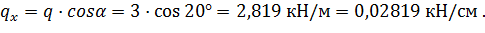
Находим значение изгибающих моментов:
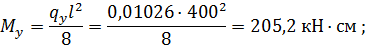
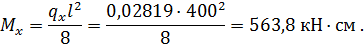
Находим моменты сопротивления относительно главных осей:
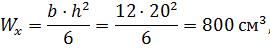
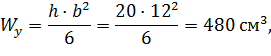
Производим проверку сечения:
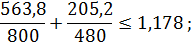
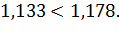
Требуемое неравенство выполняется, следовательно прочность балки обеспечена.
Дата добавления: 2021-05-28; просмотров: 413;











