Статический метод определения критических нагрузок
При проектировании инженерных сооружений обычных расчетов на прочность бывает недостаточно для того, чтобы получить полное представление о надежности сооружений, ее безопасной эксплуатации.
Наряду с задачами прочности должны быть решены проблемы устойчивости сооружения.
Расчет на устойчивость проводят либо для определения величины критической нагрузки для отдельных стержней, либо для исследования устойчивости сооружения в целом с помощью критического параметра.
Расчеты на устойчивость статическим методом проводят обособленно от указанных выше расчетов на прочность, являющихся основными.
Исследование устойчивости ведутся при следующих допущениях:
- рассматривают только узловое приложение нагрузки, при этом поперечный изгиб стержней отсутствует;
- стержни рамы считают нерастяжимыми и несжимаемыми;
- расстояния между узлами при деформациях неизменяемые (это допущение применяют только при статическом методе расчета).
Сущность статического метода заключается в том, что упругая система рассматривается в равновесии при таком деформированном состоянии, которое отличается от заданного наличием бесконечно малых перемещений, вызывающих новый, отличный от заданного, вид деформаций.
При расчете рам на устойчивость могут быть использованы методы сил и перемещений, но второй считают более предпочтительным. Аналогично, как и при решении задач статики, метод перемещений эффективнее в том случае, когда имеется набор решений для элементарных состояний, взятых из таблиц характерных эпюр и формул определения их ординат.
При расчете на устойчивость по методу перемещений выбор основной системы не отличается от выбора основной системы при обычном статическом расчете этим методом.
Так как рассматриваются рамы только с узловой нагрузкой, которая до момента потери устойчивости вызывает лишь сжатие, то реакции в фиктивных связях равны нулю и система канонических уравнений представляется однородной:
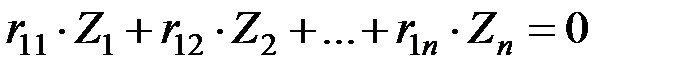 ;
;
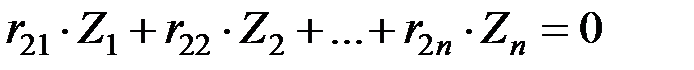 ; (157)
; (157)
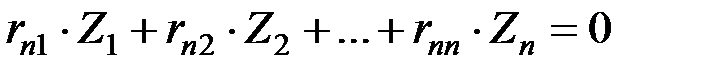 ,
,
где 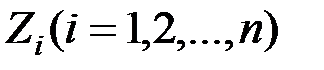 – неизвестные угловые и линейные перемещения;
– неизвестные угловые и линейные перемещения; 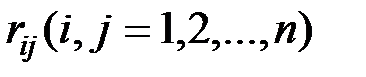 – коэффициенты метода перемещений, которые зависят от продольных усилий в стержнях;
– коэффициенты метода перемещений, которые зависят от продольных усилий в стержнях; 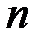 – число введенных связей в основной системе.
– число введенных связей в основной системе.
Система отвечает условиям однородности, если не считать поперечную нагрузку в стержнях чисто сжатой рамы. Моменту потери устойчивости соответствует неравенство нулю неизвестных перемещений. Следовательно, детерминант из коэффициентов 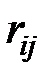 должен быть равен нулю.
должен быть равен нулю.
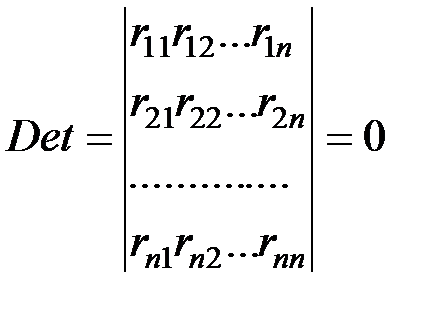 . (158)
. (158)
Раскрытие детерминанта приводит к уравнению, называемому уравнением устойчивости. Дальнейшее решение задачи состоит в отыскании значений нагрузок на раму, удовлетворяющих уравнению (158). Наименьшая из них будет критической нагрузкой.
Подробный алгоритм расчета рам на устойчивость с помощью динамического критерия изложен в книгах: Дуккарта А.В. Динамический расчет балок и рам: учебное пособие для вузов/М.: Изд-во АСВ.2002.-144 с. Кадисова Г.М. Динамика и устойчивость сооружений. - М.: АСВ,2007.-272 с.; Масленникова А.М. Основы динамики и устойчивости стержневых систем. М., Изд-во АСВ, 2008.- 346с. и других книгах.
Алгоритм расчета рам с помощью типовых эпюр и статического критерия
Рассмотрим алгоритм расчета рам с помощью статического критерия и типовых эпюр. Для этого возьмем рамы с различным количеством стоек и различными закреплениями. Нашей задачей будет найти критическую силу.
Рама с одной сжатой стойкой
Требуется найти критическую силу для рамы с одной сжатой стойкой, представленной на рис. 92, где указаны размеры и жесткости элементов рамы.
Рис. 98 Расчетная схема рамы с шарниром и со сжатой стойки
Число лишних неизвестных равно двум: угол поворота жесткого узла и линейное горизонтальное смещение ригеля.
На рис. 99 показаны основная система, единичная эпюра 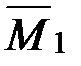 и ее характерные ординаты.
и ее характерные ординаты.
Ординаты определены согласно данным прил. 1.
Рис. 99 Расчетная схема рамы с эпюрой М1
На рис. 100 представлена единичная эпюра 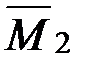 и ее характерные ординаты.
и ее характерные ординаты.
Погонные жесткости стержней 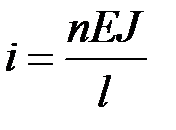 ,
,
где  – кратность жесткости стержня.
– кратность жесткости стержня.
Следовательно, 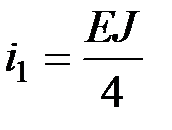 ;
; 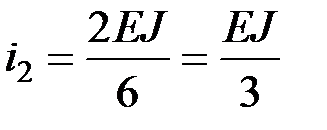 ;
; 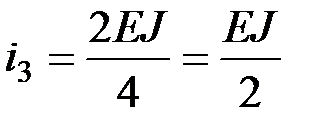 .
.
Рис. 100 Расчетная схема рамы с эпюрой М2
Используя данные эпюр 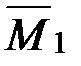 (см. рис. 99),
(см. рис. 99), 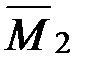 (рис. 100) и прил. 1, определим коэффициенты
(рис. 100) и прил. 1, определим коэффициенты 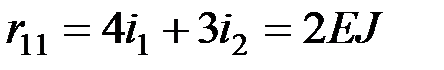 ;
; 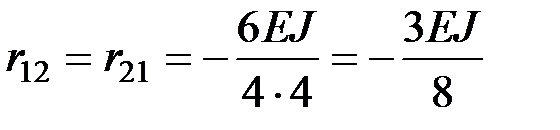 .
.
Коэффициент определяют исходя из схемы равновесия ригеля (рис. 101):
Рис. 101 Определение коэффициентов исходя из схемы равновесия ригеля
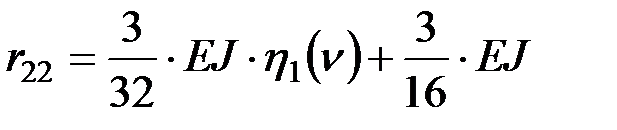 .
.
Подставив коэффициенты в определитель (2) и сократив все члены на 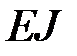 , получим
, получим
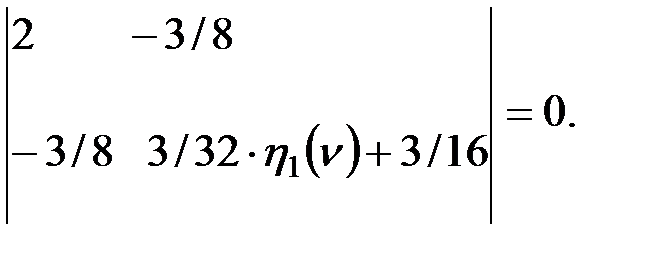
При раскрытии определителя, функция влияния продольной силы имеет вид 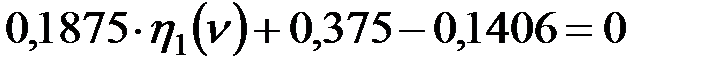 или
или 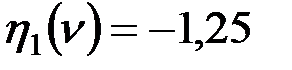 .
.
По прил. 2 находим критический параметр 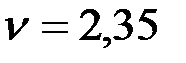 .
.
Таким образом, критическая сила будет равна:
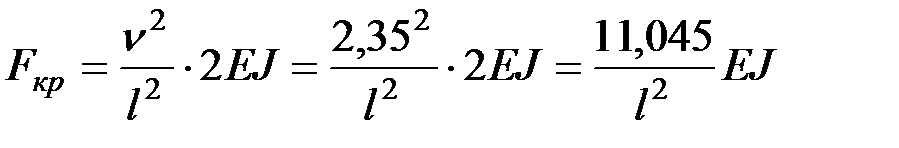 .
.
Рама с сжатой стойкой жесткого узла
Определить критическую силу для сжатой стойки рамы, показанной на рис. 102 с указанными жесткостями стержней и их размерами.
В отличие от предыдущего примера продольная сила приложена в жестком узле. Число лишних неизвестных также равно двум.
Рис. 102 Расчетная схема рамы
Основная система и эпюры моментов от единичных смещений показаны на рис. 103 и рис. 104. Построение этих эпюр произведено в соответствии с данными прил. 1.
Рис. 103 Расчетная схема рамы с эпюрой М1
Коэффициенты канонических уравнений: 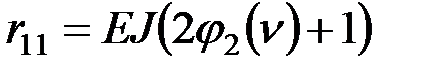 ;
; 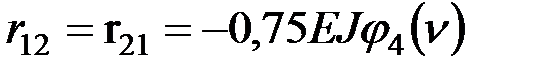 ;
; 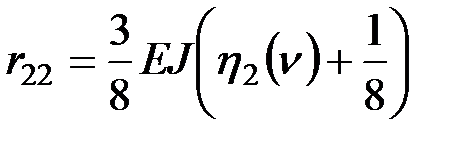 .
.
Рис. 104 Расчетная схема рамы с эпюрой М2
Подставим коэффициенты 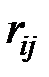 в определитель. Раскрытый определитель, в соответствие с выражением (3), представляет трансцендентное уравнение (так называемое уравнение устойчивости).
в определитель. Раскрытый определитель, в соответствие с выражением (3), представляет трансцендентное уравнение (так называемое уравнение устойчивости).
Открывая его методом подбора, найдем минимальное значение критического параметра  :
:
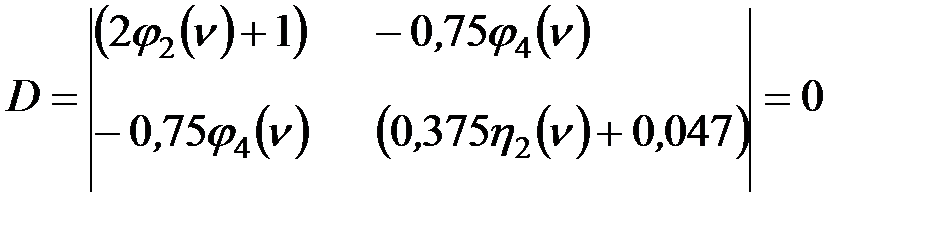 . (159)
. (159)
Или в раскрытом виде имеем:
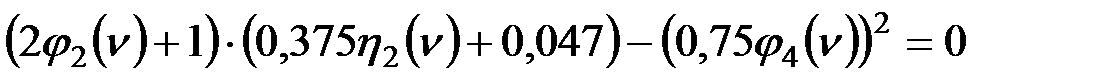 .
.
Далее необходимо найти такое значение параметра 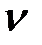 , при котором определитель обратится в нуль. Параметр
, при котором определитель обратится в нуль. Параметр 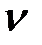 изменяется в пределах
изменяется в пределах
( 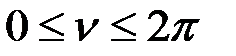 ).
).
Задаем значения, близкие к среднему, 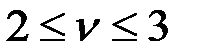 . Определяем функции учета продольных сил согласно прил. 2. Данные приведены в табл. 1.
. Определяем функции учета продольных сил согласно прил. 2. Данные приведены в табл. 1.
Таблица 1
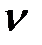
| 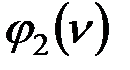
| 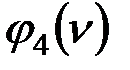
| 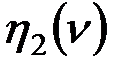
| D |
| 0,8590 | 0,9311 | 0,5980 | 2,718 -0,6983 -0,6983 0,2713 = 0,2497 | |
| 0,6560 | 0,8393 | 0,0893 | 1,312 -0,6295 -0,6295 0,0893 = -0,2906 |
Построим график зависимости 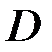 от
от 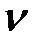 методом линейной интерполяции (рис. 105). Находим
методом линейной интерполяции (рис. 105). Находим 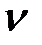 , близкое к фактическому. При
, близкое к фактическому. При 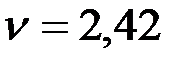 определитель (159) превращается в ноль.
определитель (159) превращается в ноль.
Рис. 105 График определения зависимости 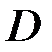 от
от 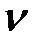 методом линейной интерполяции
методом линейной интерполяции
Таким образом, критическая сила будет равна:
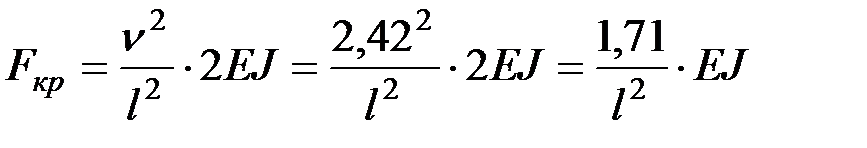 .
.
Рама с шарнирным закреплением ригеля
На рис. 106 показана рама с двумя сжатыми стойками. Найдем критические силы при заданных размерах и жесткостях элементов.
Рис. 106 Расчетная схема рамы с двумя сжатыми стойками
Основная система изображена на рис. 107
Рис. 107 Основная система
На рис. 108 и рис. 109 представлены единичные эпюры моментов от поворотов жестких узлов рамы на 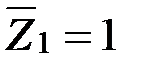 и
и 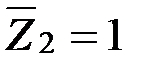 .
.
Рис. 108 Расчетная схема рамы с эпюрой М1
Рис. 109 Расчетная схема рамы с эпюрой М2
Критические силы для каждой стойки будут различны, следовательно, критические параметры (с учетом коэффициента приведения) соответственно равны:
– для первой стойки 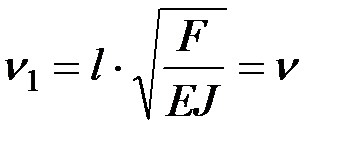 ;
;
– для второй стойки 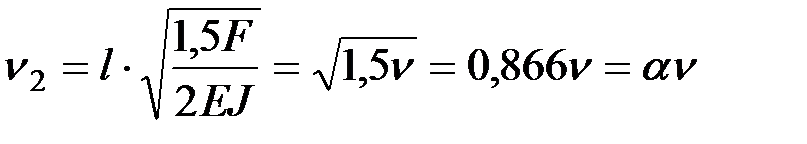 .
.
Уравнение устойчивости запишем в следующем виде:
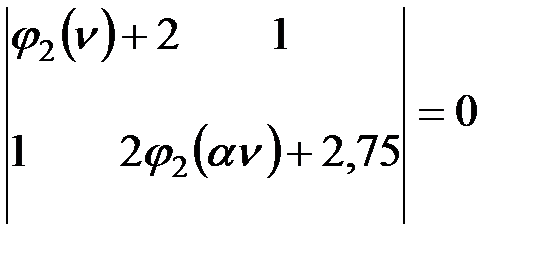 ;
;
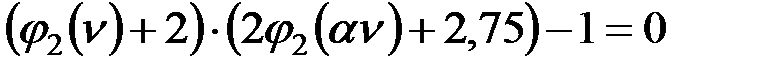 ;
;
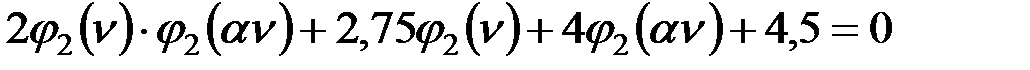 . (160)
. (160)
Решение такого уравнения следует проводить путем подбора.
Прежде следует задаться начальным параметром  . Подставим значения функций в уравнение (4) и определим в каких пределах его можно изменять. Обе стойки рамы находятся в таких условиях, что их верхние концы не могут смещаться горизонтально, но упруго поворачиваются в узлах. Следовательно, критические силы стоек будут близки к критической силе прямолинейного стержня с заделкой обоих концов. Критический параметр в этом случае
. Подставим значения функций в уравнение (4) и определим в каких пределах его можно изменять. Обе стойки рамы находятся в таких условиях, что их верхние концы не могут смещаться горизонтально, но упруго поворачиваются в узлах. Следовательно, критические силы стоек будут близки к критической силе прямолинейного стержня с заделкой обоих концов. Критический параметр в этом случае 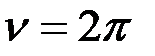 .
.
Первоначально примем значение критического параметра в пределах 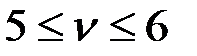 . Согласно табл. 2 имеем два значения функций
. Согласно табл. 2 имеем два значения функций
Таблица 2
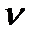
| 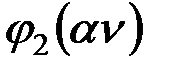
| 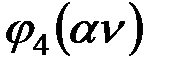
| D |
| -0,4772 | 0,1285 | 1,5228 1 1 3,2614 = 4,3831 | |
| -5,1589 | -0,763 | -5,1589 1 1 1,987 = -9,2504 |
Построим график зависимости 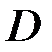 от
от 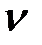 и методом линейной интерполяции (рис. 110) находим
и методом линейной интерполяции (рис. 110) находим 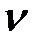 . При
. При 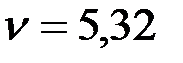 уравнение (160) обращается в ноль.
уравнение (160) обращается в ноль.
Рис. 110 Построение графика зависимости 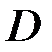 от
от 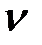 методом линейной интерполяции
методом линейной интерполяции
Следовательно, критические силы равны:
– для первой стойки 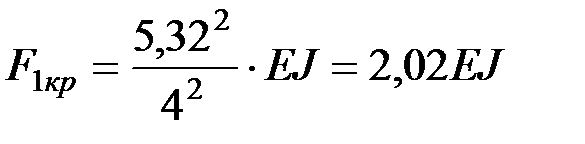 ;
;
– для второй стойки  .
.
Рама из трех стоек с загружением в шарнирных узлах
Рассмотрим пример определения критических сил для рамы, представленной на рис. 111. Основная система изображена на рис. 112.
Рис. 111Расчетная схема рамы Рис. 112 Основная система
Критические параметры для каждой стойки равны:
– для первой стойки 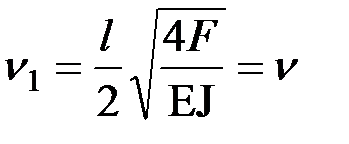 ;
;
– для второй стойки 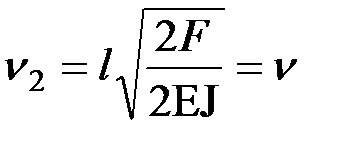 .
.
Эпюры единичных моментов изображены на рис. 113 и 114.
Коэффициенты уравнения устойчивости:
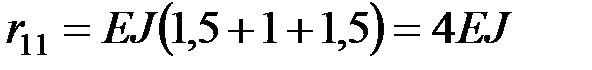 ;
; 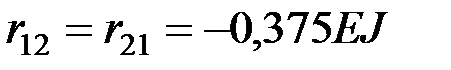 ;
; 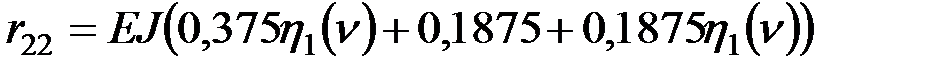 .
.
Рис.113 Расчетная схема рамы с эпюрой М1
Рис. 114 Расчетная схема рамы с эпюрой М2
Уравнение устойчивости запишем в следующем виде:
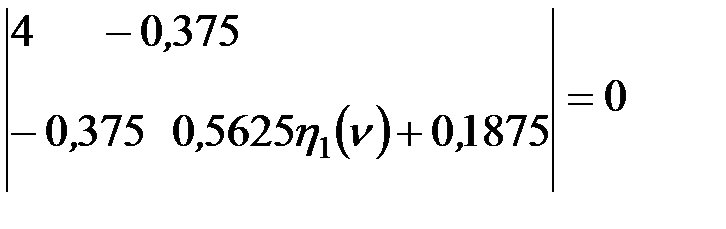 .
.
Раскрытие его приводит к простому уравнению:
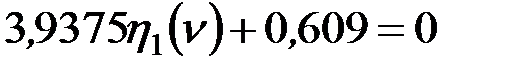 .
.
Отсюда находим 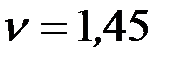 и
и 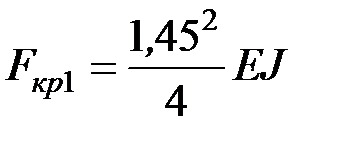 ,
, 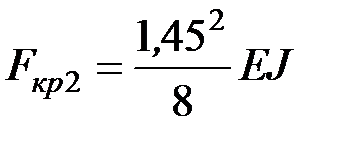 .
.
Рама с загружением центральной и крайней стоек
На рис. 115 изображена рама с двумя сжатыми стойками с заданными размерами и жесткостями элементов. Основная система дана на рис. 116.
Критические параметры:
– для первой стойки 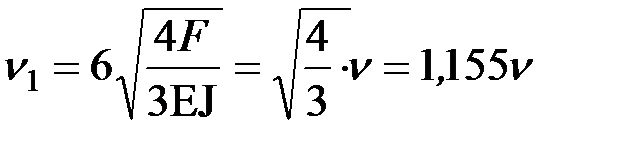 ;
;
– для второй стойки 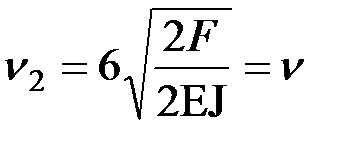 .
.
Рис. 115 Расчетная схема рамы с тремя стойками
Рис. 116 Основная система
Единичные эпюры моментов от поворота жесткого узла на 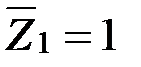 и линейного смещения узлов ригеля на
и линейного смещения узлов ригеля на  показаны на рис. 117 и 118.
показаны на рис. 117 и 118.
Рис. 117 График построение эпюры М1
Рис. 118 График построение эпюры М2
Коэффициенты уравнения устойчивости:
 ;
; 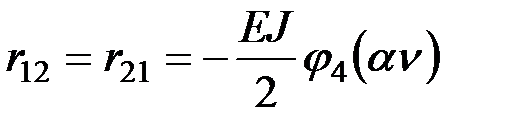
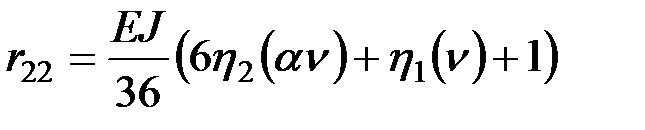 .
.
Определитель уравнения устойчивости:
 .
.
Раскрыв определитель, получим трансцендентное уравнение, которое решается путем подбора критического параметра 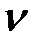 .
.
Таблица 3
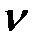
| 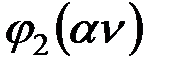
| 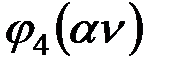
| 
| 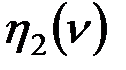
| D |
| 0,8099 | 0,9083 | -1,1861 | 0,598 | 3,6198 -0,4542 -0,4542 0,0945 = 0,1358 | |
| 0,5194 | 0,7821 | -2,8639 | -0,2100 | 3,0388 -0,3911 -0,3911 -0,0576 = -0,2227 |
Примем значение критического параметра 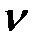 в следующим пределе:
в следующим пределе: 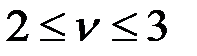 .
.
Критический параметр для коэффициентов 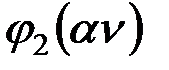 ,
, 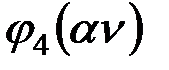 ,
, 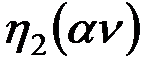 умножается на
умножается на 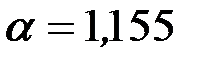 .
.
Согласно табл. 3 определяем критические параметры и значения определителя 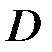 .
.
Построим график изменения величин 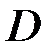 при
при 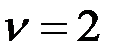 и
и 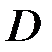 при
при 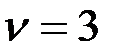 , считая их изменяющимися по линейной зависимости (см. рис. 119).
, считая их изменяющимися по линейной зависимости (см. рис. 119).
Сближая постепенно границы между 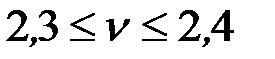 , получим искомую величину
, получим искомую величину 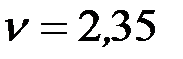 , при которой определитель
, при которой определитель 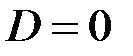 .
.
Рис. 119 График изменения величин 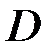 при
при 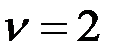 и
и 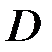 при
при 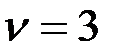
Таким образом, критические силы равны:
– для первой стойки 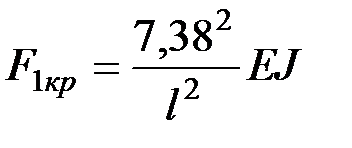 ;
;
– для второй стойки 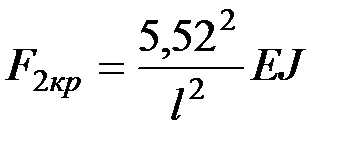 .
.
| <== предыдущая лекция | | | следующая лекция ==> |
| Расчёт на устойчивость статически определимых рамных и балочных систем. | | | Общие понятия теории устойчивости сооружений. |
Дата добавления: 2017-01-26; просмотров: 3278;











