Нормальное поле силы тяжести

В гравиразведке нас интересуют прежде всего аномальные значения силы тяжести, но для их получения необходимо знать нормальные значения поля на поверхности Земли.

Точные значения потенциала силы тяжести определить невозможно, так как неизвестны расположение масс в Земле и ее точная фигура. Первым приближением Земли является сфера, второе приближение – эллипсоид вращения с малым сжатием (сфероид). При геодезических работах в качестве поверхности относимости для Земли используется эллипсоид Красовского со сжатием α = (a-b)/a = 1/298,3 , где a и b соответственно большая и малая полуоси эллипсоида.

В гравиразведке в качестве нормального поля используют некоторую уровенную (эквипотенциальную) поверхность, в каждой точке которой сила тяжести направлена по нормали. Эта поверхность совпадает с невозмущенной ветром и течениями поверхностью океана и продолжается под поверхностью континентов так, что в любой его точке сила тяжести направлена по нормали. Такая поверхность называется геоидом и принимается за фигуру Земли. Совпадая на океанах с физической поверхностью Земли, геоид представляет собой следующее после эллипсоида приближение к истинной фигуре Земли именно на океанах. На континентах переход от эллипсоида к геоиду не решает задачи следующего приближения, т. к. геоид является фигурой неправильной и, в отличие от эллипсоида, не может быть выражен аналитически, что исключает его использование при решении геодезических задач. При выводе формул нормального распределения силы тяжести некоторые авторы одновременно вычислили и построили карты отклонений геоида от сфероида (рис. 2.7).

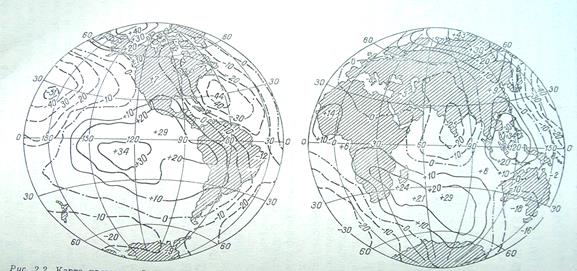
Рис. 2.7. Карта превышений геоида В. Каула ( в метрах) над сфероидом со сжатием 1/284,26 (по Миронову,1980)

Для сфероида в 1743 году французский ученый А. Клеро получил формулу нормального поля силы тяжести с точностью до малых второго порядка:

γ_о = g_e(1+β sin² φ),(2.26.)

где β = (g_p – g_e)/g_e – относительный избыток силы тяжести на полюсе g_p по отношению к силе тяжести на экваторе g_e, φ – широта точки наблюдения. Определив силу тяжести в двух точках земной поверхности с широтами φ₁ и φ₂ , можно составить два уравнения с двумя неизвестными g_e и β. Для более точного определения этих величин решают систему для большого количества пунктов методом наименьших квадратов.

Точная формула распределения силы тяжести на сфероиде была предложена итальянским геодезистом К. Сомильяна:

γ_о = (a g_e cos² φ + b sin²φ)(a² cos²φ +b² sin² φ)^-1/2. (2.27)

Если в правой части этого равенства сделать подстановку β = (g_p – g_e)/g_e и α = (a-b)/a и разложить в ряд до малых третьего порядка, получим уточненную формулу Клеро :

γ_о = g_e(1+β sin² φ + β₁ sin² 2φ). (2.28)

Численные значения коэффициентов g_e ,β , β₁ находят сравнением формулы (2.28) с результатами гравиметрических наблюдений. Формулы нормального распределения силы тяжести выводились многими авторами (Грушинский Н.П., Жонголович И.Д., Уотила У., Хейсканен У. и др.) но сейчас только две из них применяются в гравиразведочной практике:

1. Формула Гельмерта выведена по результатам более 1600 измерений силы тяжести, распределенных по 9 широтным зонам, каждая из которых была разделена на 10-градусные трапеции. Она имеет вид

γ_о = 978030 (1 + 0,005302 sin²φ – 0.000007 sin² 2φ) -14 мГл. (2.29)

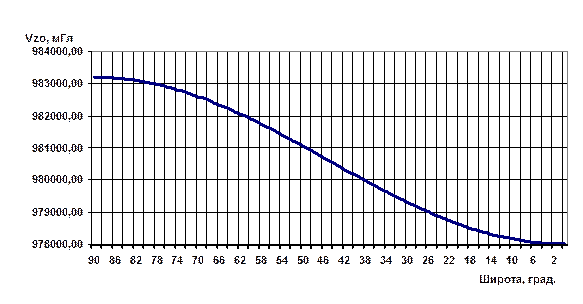
Рис. 2.8. График значений нормального поля, рассчитанных по формуле Гельмерта.

Для привязки к новой Потсдамской системе здесь введена поправка – 14 мГл. График нормальных значений, полученных по формуле Гельмерта, приведен на рис. 2.8. Для Томска, где широта φ = 56^о 26^I нормальное значение γ_о = 981610,46 мГл. Несмотря на то, что эту формулу считают устаревшей, она до сих пор применяется в России и странах бывшего СССР и СЭВ. Это связано с тем, что соответствующий ей эллипсоид имеет сжатие, близкое к эллипсоиду Красовского. Кроме того, по современным данным, полученным в результате изучения вариаций элементов орбит искусственных спутников, сжатие Земли α также весьма близко к эллипсоиду Красовского и составляет 1/298,25. Переход на новую формулу потребовал бы большой вычислительной работы.

2. В 1930 году на Международном геодезическом конгрессе в Стокгольме в качестве международной была принята формула Кассиниса для сфероида со сжатием α = 1/297:

γ_о = 978049 (1 + 0,0052884 sin²φ – 0.0000059 sin² 2φ). (2.30)

Эта формула применяется в большинстве стран Европы и Америки.

В 1971 году на ассамблее Международного союза геофизики и геодезии в Москве была рекомендована новая формула нормального распределения силы тяжести, соответствующая так называемой референц-системе 1967 года:

γ_о = 978031,8 (1 + 0,005024 sin²φ – 0.0000059 sin² 2φ). (2.31)

Для перехода от формулы Кассиниса к системе 1967 года надо вносить поправку, равную (-17,2 + 13,6 sin²φ) мгл.

Расхождение значений g_e и β по разным формулам объясняется недостаточной гравиметрической изученностью Земли. С накоплением данных будут появляться новые, все более точные формулы.