Векторная диаграмма трансформатора

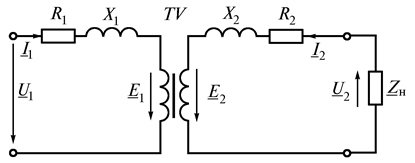В реальном трансформаторе в отличие от идеального учитываются актив­ные сопротивления обмоток, магнитные потоки рассеяния обмоток и потери мощности в стали. На рис. 9.4 активные сопротивления 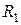и и 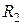индуктивные

Рис. 9.4

сопротивления 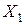и 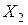от потоков рассеяния выделены отдельно, а обмотки показаны идеальными без этих сопротивлений. Согласно второму закону Кирх­гофа уравнения для первичных и вторичных цепей в комплексной форме имеют вид

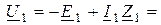
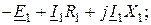
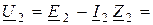
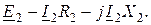(9.7)

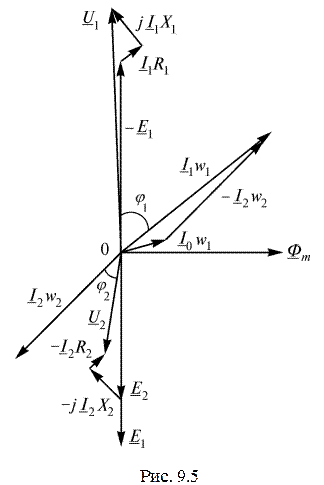
Этим уравнениям соответствует векторная диаграмма (рис. 9.5), построенная для активно-индуктивной нагрузки 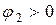. Из анализа диаграммы при переменной нагрузке следует, что с увеличением вторичного тока уве­личиваются ток первичной обмотки и коэффициент мощности.

9.4. Схема замещения трансформатора

Электрические цепи с трансформаторами сложно рассчитывать из-за маг­нитной связи между обмотками. Поэтому трансформатор представляют схемой замещения, в которой магнитная связь заменяется электрической цепью. С этой целью обе обмотки «приводят» к одному числу витков, обычно к числу витков первичной обмотки. Приведенные параметры вторичной цепи обозначают бук­вами со штрихом.

Применение схемы замещения трансформатора предполагает, что мощности:

передаваемая во вторичную цепь

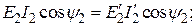(9.8)

отдаваемая приемнику

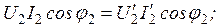(9.9)

затрачиваемая на нагрев обмотки

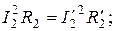(9.10)

не изменяются, а углы сдвига 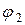и 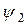и соотношение между индуктивными и активными сопротивлениями обмоток

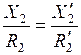. (9.11)

Так как 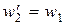, то

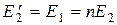. (9.12)

Из (9.8) и (9.12) следует

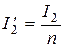. (9.13)

Совместное решение (9.10, 9.11, 9.12) дает

. (9.14)

Равенство ЭДС первичной и вторичной обмоток позволяет объединить их электрические цепи в одну цепь (рис. 9.6). Этот участок цепи называют вет­вью намагничивания. В ней 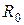– активное сопротивление, учитываю­щее

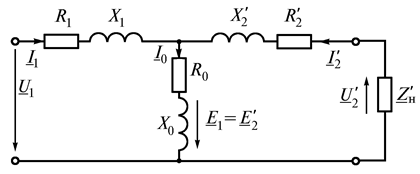Рис. 9.6

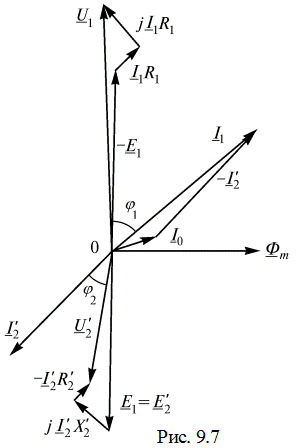потери мощности в стали, 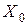– реактивное сопротивление, обусловленное основным магнитным потоком. В силу равенства 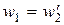на векторной диа­грамме (рис. 9.7) показаны не МДС, а токи

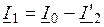. (9.15)

Если пренебречь током холостого хода 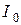и удалить из схемы (рис. 9.6) ветвь намагничивания, то получим упрощенную схему замещения (рис. 9.8 а), а с учетом 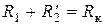и 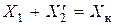– схему (рис. 9.8 б).

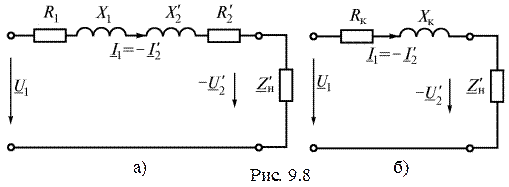
Упрощенной схеме замещения соответствует векторная диаграмма на рис. 9.9. Такую схему используют при нагрузке, близкой к номинальной.