Прямая и обратная задачи для вертикально намагниченного горизонтального цилиндра бесконечного простирания.
Пусть на глубине 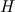 параллельно оси y расположен бесконечно длинный цилиндр с магнитным моментом единицы длины, равным
параллельно оси y расположен бесконечно длинный цилиндр с магнитным моментом единицы длины, равным 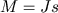 , где
, где 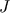 - интенсивность намагничивания, постоянная для всего цилиндра и направленная вертикально,
- интенсивность намагничивания, постоянная для всего цилиндра и направленная вертикально,  - поперечное сечение цилиндра (рис. 2.7). Требуется определить напряженность поля вдоль оси
- поперечное сечение цилиндра (рис. 2.7). Требуется определить напряженность поля вдоль оси  . Поле такого цилиндра можно считать эквивалентным полю бесконечного числа вертикальных магнитных диполей, центры которых расположены по оси цилиндра.
. Поле такого цилиндра можно считать эквивалентным полю бесконечного числа вертикальных магнитных диполей, центры которых расположены по оси цилиндра.

|
| Рис. 2.7. Магнитное поле горизонтального цилиндра бесконечного простирания |
Потенциал в точке 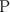 от элементарного диполя определяется согласно уравнению (2.5):
от элементарного диполя определяется согласно уравнению (2.5):

|
где 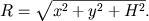
Потенциал всего цилиндра равен потенциалу от системы диполей, расположенных вдоль оси бесконечного цилиндра, или интегралу по объему цилиндра от выражения для потенциала элементарного диполя:
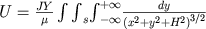
|
Так как  , то
, то 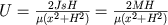 и
и
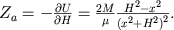
| (2.14) |
Легко видеть, что при  будет максимум
будет максимум 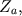 а при
а при 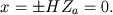 При
При 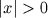 значения
значения 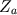 будут отрицательны, при
будут отрицательны, при 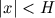 - положительны.
- положительны.
В плане над горизонтальным цилиндром будут вытянутые аномалии двух знаков.
При решении обратной задачи глубину залегания цилиндра можно определить по формулам: 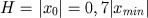 , где
, где 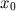 и
и 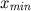 - абсциссы точек, в которых
- абсциссы точек, в которых 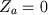 и
и 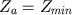 . Зная
. Зная  , можно найти погонную массу цилиндра
, можно найти погонную массу цилиндра 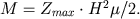 Заменив
Заменив 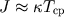 , получим
, получим 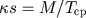 . Зная
. Зная 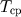 и
и 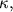 можно рассчитывать площадь сечения цилиндра.
можно рассчитывать площадь сечения цилиндра.
Дата добавления: 2021-05-28; просмотров: 542;











