Развитие народного образования в1786-1800 гг.
| Годы | ||||||
| Кол-во училищ | ||||||
| Численность учителей | ||||||
| Численность учащихся |
Школьная реформа 1780 - годов была первой попыткой создать государственную систему народного образования. В основу новой школы были положены принципы всесословности и бесплатности обучения, но для создания системы образования не хватило и, что самое главное, не было еще потребности в образовании у широких слоев населения. Решение всех этих задач было делом следующего столетия.
В XVIII веке сложилась государственная система образования:
· приходские школы (1 год),
· уездные школы (2 года),
· гимназии (4 года),
· университеты.
Всего в конце XVIII в. в России насчитывалось около 550 различных учебных заведений с числом учащихся до 62 тыс. человек. Из них около 400 народных училищ, свыше 60духовных семинарий и школ и около 60 закрытых дворянских учебных заведений.
Необходимо отметить, что Санкт-Петербургская Академия наук в XVIII в. внесла определяющий вклад в культурно-образовательную жизнь России, выступая в качестве мощного источника идей, постоянно выдвигая оригинальные просветительско-образовательные проекты. Академия наук способствовала осознанию обществом и правительством необходимости масштабных просветительских преобразований и указала главные направления коренных изменений школьного дела в России. Это позволило к концу XVIII в. добиться существенных успехов в сфере просвещения и заложить основу для дальнейшего развития образования, науки и культуры в целом.
б) Математика в Московском университете
Московский университет стараниями М.В. Ломоносова был основан в 1755 г., и при нём сразу же были открыты 2 гимназии – для дворян и для разночинцев. Каждая из них делилась на 4 группы предметов - «школы», причём 2 из них «российская» и «латинская» были обязательными, а 2 другие – «школа первых оснований наук» и «школа знатнейших европейских языков» (немецкая и французская) - по выбору. В двух последних, кроме языков, изучались «науки» (арифметика, геометрия, география, история). В дворянской школе изучались ещё необязательные предметы – военная и гражданская архитектура, теоретическая и экспериментальная физика, алгебра и др.
В первое десятилетие подготовку в университет осуществляла разночинная гимназия, дворянская же была самостоятельным учебным учреждением, но позднее преподавание в обеих гимназиях шло по одному учебному плану, где математика была сначала «второстепенна». Это определялось самим профилем университета, где были только 3 факультета: юридический, медицинский и философский. Математику изучали на всех факультетах достаточно поверхностно. Сначала Московский университет был профессиональной школой для подготовки врачей, юристов, чиновников и учителей. Поскольку выпускники гимназий не все шли учиться в университет, то студентов там периодически не хватало, их набирали из числа лучших учеников духовных семинарий.
В Московском университете под термином «чистая математика» понималась совокупность арифметики, геометрии, тригонометриииалгебры, прикладная математика представляла собой довольно сжатое изложение астрономии, механики, гномоники, оптики, гидравлики, архитектуры и некоторых других наук. Но это не означало, что Московский университет давал подготовку более низкого уровня, чем западные университеты. Последние не имели ни установленных программ, ни общепринятых учебных планов, а сумма знаний, передаваемая студентам, сильно зависела от личности преподавателя.
Первым преподавателем математики в Московском университете былАнтон Алексеевич Барсов (1730-1791)– выпускник Славяно-греко-латинской Академии, в числе лучших отправленный после окончания в академический университет. Там он выделился своими успехами в математике и словесных науках. В 1753 году по окончании университета Барсов получил звание магистра философии и свободных наук. Он продолжал изучать философию и языки, занимался переводами научных трудов, преподавал в академическом университете математику.
В 1755 г. Барсов перешёл в Московский университет. Сначала он читал лекции по алгебре, но в 1761 г. передал преподавание своему ученику Д.С. Аничкову и перешел на кафедру словесности, где в течение 30 лет являлся ординарным профессором кафедры красноречия и читал курсы грамматики, риторики и поэзии.
Иван Акимович Рост (1726-1791) (Иоганн-Иоахим-Юлиус) - профессор Московского университета, воспитанник Геттингенского университета, в 1757 г. был приглашён на должность адъюнкта сначала для преподавания английского языка, а затем математических дисциплин (на латыни). С 1761 г. он сделался ординарным профессором и стал преподавать прикладную математику и экспериментальную физику. Разделение это, однако же, не было строгим. Были годы, когда к предметам своего обычного преподавания Рост присоединял еще и некоторые из отделов чистой математики, причём никакого определенного порядка в их следовании друг за другом не соблюдалось. К ним нередко были присоединяемы профессором еще и геодезия, подземная геометрия, артиллерия, учение о трении и гидротехника.
Нужно отметить, что Рост был скорее замечательным лингвистом, чем математиком, он знал теоретически и практически 8 языков (латинский, греческий, французский, немецкий, английский, голландский, итальянский и испанский). В 1788 г. Рост начал издавать первый московский журнал по естественным наукам - «Магазин натуральной истории, физики и химии».
Учениками Роста были Аршеневский и Панкевич. Василий Кондратьевич Аршеневский (1758-1808) - начальное образование получил в Киеве, в 1774 году приехал в Москву, учился в гимназии у Роста и Аничкова, затем по окончании преподавал математику в той же гимназии, а с 1795 г. – в университете. С 1788 года начал читать университетские лекции - по геометрии, тригонометрии и алгебре, потом - о конических сечениях; заменил умершего Д. С. Аничкова на кафедре математики. В 1789 году был назначен адъюнктом, а в 1795 году - экстраординарным профессором, и, наконец, в 1805 году стал ординарным профессором по кафедре чистой математики. Это был первый профессор Московского университета, начавший (в 1800 г.) читать элементы высшей математики.
Математических трудов он никаких не оставил; напечатаны только две речи его, произнесенные им в публичных собраниях Московского университета:
ü «О начале, связи и взаимном пособии математических наук и пользе оных» (1794),
ü «О связи чистой математики с физикою» (1802).
Почти одновременно с ним в Московском университете учился и другой киевлянин – Панкевич Михаил Иванович (1757-1812),после окончания университета защитивший магистерскую диссертацию «Об особенных гидравлических машинах, которыми с помощью действия упругих паров воды и давления атмосферы вода может быть поднята до чрезвычайной высоты и проч.» (1788). После смерти И.А. Роста он занял кафедру прикладной математики и читал математику, оптику, сферическую и теоретическую астрономию.
Один из слушателей Панкевича, П. С. Щепкин, отметил в своём дневнике:
«… в сем знаменитом человеке университет потерял твердую свою опору. Ему обязан я привязанностью своей к математическим наукам; наиболее же старался подражать умеренности жизни его». М. И. Панкевич погиб в рядах ополчения 1812 года при обороне Москвы, а архивы, особенно богатые у Аничкова и Аршеневского, погибли в пожаре 1812 года.
Дмитрий Сергеевич Аничков (ок. 1738-1788) - русский философ-просветитель, логик, публицист, оставивший значительно больший след в истории русской математической культуры, чем его предшественники по МУ. Выходец из семьи подьячего Троице-Сергиевской лавры учёбу начал в лаврской семинарии, в 1755 г. в числе 6 лучших учеников переведён в новооткрытый Московский университет. За время учёбы в университете получил 5 золотых медалей за успехи, успешно его окончил в звании магистра (1762). Биографы сходятся во мнении, что он отличался не столько блестящими способностями, сколько трудолюбием, неутомимостью и основательностью познаний.
В том же 1762 г. он начал преподавать тригонометрию и алгебру в гимназии при Московском университете и в самом университете геометрию и тригонометрию, а через 3 года получил кафедру философии и логики. В научном плане философия была ему ближе, чем математика. В 1771 г. ему было присуждено звание экстраординарного, а в 1777 г. - звание ординарного профессора логики, метафизики и чистой математики.
В истории отечественного школьного математического образования Аничков оставил заметный след, прежде всего, как автор многих учебников, созданных для Московского университета и гимназии при нём. В середине 60-х годов сложилось катастрофическое положение с учебниками математики: библиотека университета могла предложить только книги на латыни (Вейдлера, Крафта, Вольфа и Штурма), на русском был только перевод Евклида. Аничков тогда перевёл и издал целую серию учебных руководств Вейдлера, представлявших собой сокращения учебников Х. Вольфа: «Аналитика специоза или алгебра», «Арифметика теоретическая и практическая», «Геометрия теоретическая и практическая», «Плоская тригонометрия», «Военная архитектура или фортификация», решив проблему нехватки учебных математических пособий (1765).
Однако, он понимал, что нужны новые учебники, учитывающие современные достижения математики. Оставаясь в методическом отношении проводников идей Вольфа, он сумел создать свои собственные учебники, содержание которых отличалось от учебников Вейдлера и Вольфа:
ü 1764 г. – «Теоретическая и практическая арифметика, в пользу и употребление юношества, собранную из разных авторов»,
ü 1780 г. – «Теоретическая и практическая геометрия…», «Теоретическая и практическая тригонометрия…»
ü 1781 г. – «Начальные основания алгебры, или арифметики литеральной.
По мнению специалистов, наиболее удачен из них учебник по арифметике, он переиздавался 4 раза. Несмотря на сухость изложения, характерную для методики Вольфа, учебники Аничкова сыграли довольно значительную роль в постановке математического образования в МУ.
в) Математика в русских военных и инженерных школах
К 50-м годам все отрасли военного образования – морское, артиллерийское, инженерное и сухопутное – были сословно-дворянскими, учеников недворянского происхождения принимала только Навигацкая школа.
В 1715 году в Санкт-Петербурге по настоянию Петра была учреждена Морская академия, или Академия морской гвардии. Морской кадетский корпус был открыт в конфискованном уже по указанию императрицы Анны Иоанновны в 1732 году. Академия и школа просуществовали до 1752 года, когда указом по образцу сухопутного был основан Морской шляхетный кадетский корпус на 360 учащихся.
Преподавание в корпусе сначала страдало многопредметностью, но обучение математике было хорошо поставлено, что объясняется историей корпуса, ведущего своё начало от Московской Навигацкой школы, первого математического заведения России. Отметим, что по штату для преподавания в корпусе математики и навигацких наук полагалось 15 человек (1 профессор, 2 учителя и при них 6 подмастерьев и 6 учеников). Профессором был приглашённый из Англии математик Ньюберн, а одним из подмастерьев стал ученик Магницкого Курганов.
Николай Гаврилович Курганов (1722-1796) - русский просветитель, педагог, математик, академик Санкт-Петербургской Академии наук, военный моряк, автор и составитель учебников. Курганов - выходец из мелкой разночинной среды, сын бедного унтер-офицера, обучался в Петербургской морской академии, после завершения обучения преподавал в Морском корпусе. В 1774 году получил степень профессора.
В 1757 году был издан учебник Курганова «Универсальная арифметика, содержащая основательное учение как легчайшим способом разныя вообще случающиеся, математике принадлежащие арифметические, геометрические и алгебраические выкладки производить» (в 2 частях). Новый учебник с восторгом был принят для преподавания в корпусе и вытеснил даже «Арифметику» Магницкого:
«…достоинства «Арифметики…» Курганова были так несомненны, написана она была таким простым и ясным языком, что знаменитый Магницкий со своим славянским языком и запутанными определениями окончательно и навсегда померк в учебной литературе».
Он переиздавался далее под разными названиями и различными изменениями, например, «Новая арифметика, или числовник, содержащий в себе все правила цыферного вычисления, случающегося в общежитии в пользу всякого учащегося, Воинского, Статского и Купеческого Юношества» (без сведений из алгебры и геометрии; 1771), «Арифметика или Числословие, …» (1776), «Генеральная арифметика…» (1794). Первое издание учебника состояло из 5 глав, из которых 1-4 включали арифметику с некоторыми приложениями к геометрии, а 5-я – алгебру. Все исследователи отмечают сходство методик Курганова и Магницкого, оба стремились составить не только учебник для школы, но и общедоступное руководство, поэтому особое внимание обращали на решение задач. Однако, У Курганова уже была современная ему учебная литература. в частности, «Арифметика» Эйлера, что заметно повлияло на характер книги и создало ей завидную известность.
В 1775 г. появилась его «Генеральная геометрия, или Общее измерение протяжения составляющее Теорию и Практику оной науки», состоящая их 3 частей и включающая лонгиметрию, планиметрию и стереометрию с плоской и сферической стереометрией. Учебник оказался труден для учения, поэтому Курганов в 1769 г. издал к нему дополнение «Элементы геометрии, то есть первые основания науки измерении протяжения, состоящие из 8 Евклидовых книг, изъясненных новым способом удобопонятнейшем юношеству» (перевод с французского подлинника, печатаннаго в Гааге 1762 года). Эта книга и была принята в корпусе в качестве учебника по геометрии.
Кроме математических работ Курганову принадлежат также работы по навигации, военному делу и русскому языку. Среди нематематических учебников самым знаменитым в свое время являлся «Письмовник, который переиздавался не менее 10 раз на протяжении почти 70 лет и содержал популярное изложение русской грамматики, а также собрание народных пословиц, поговорок, народной поэзии и стихотворений крупнейших русских поэтов XVIII века.
Нужно указать, что об образованности бывшего начальника батальона профессора Н.Г. Курганова, преподававшего в корпусе, ходили легенды. Математические и морские науки он нередко читал на французском и немецком языках, которые знал в совершенстве, отсылая к английским и латинским книгам, прочитанным им самим.
В 1731 г. в Петербурге была основана Рыцарская Академия, сначала готовившая учащихся не только к военной, но и гражданской деятельности, но в 1761 г. преобразованная в сугубо военное учебное заведение – Сухопутный шляхетский корпус.В 1784 году проверкой было установлено, что кадеты за 9 лет обучения не успевали закончить изучение арифметики, не могли овладеть геометрией и что они «…отчаиваясь, успеть во всём, ни к одной, по-видимому, затем не применялись и ни в одной не успевали».
Определённую роль в развитии русского математического образования всё же сыграли преподаватели Сухопутного корпуса – Назаров и Людевих. Степан Назаров - инженер-прапорщик (позднее титулярный советник) и преподаватель Сухопутного шляхетного кадетского корпуса, составил «для употребления обучающегося благородного юношества» Лонгеометрию", "Планометрию" и "Штир-геометрию", вторая часть - "Тригонометрию". «Практическую геометрию» (3 издания: 1760, 1767 и 1775), которая состояла главным образом в предложении и решении ряда геометрических задач, причем решения не сопровождались ни объяснениями, ни доказательствами. Первая часть книги обнимала "Лонгеометрию", "Планометрию" и "Штир-геометрию", вторая часть - "Тригонометрию". Карл фон Людвих издал «Краткое руководство к арифметике» (1758).
Две военные школы – Артиллерийская и Инженерная – в 1758 году были слиты воедино и названы впоследствии Артиллерийским инженерным шляхетным корпусом (1762 г.) по плану М.И Мордвинова.
Михаил Иванович Мордвинов (1730-1782) - инженер-генерал, известный военный педагог и деятель царствования Императрицы Екатерины II, воспитанник Сухопутного корпуса. откуда был выпущен в 1747 инженер-прапорщиком. В 1756 он был назначен заведующим Инженерной школой, а после соединении её с Артиллерийской - начальником этой Инженерно-артиллерийской школы, которую довел до отличного состояния. В числе его учеников были не только прославленные генералы, как М.И. Кутузов, но и видные математики и методисты: С.Е. Гурьев, В.И. Висковатов, Н.В. Верещагин. Особое внимание в плане перестройки корпуса Мордвинов уделил постановке преподавания математических наук, в частности, он включил механику, арифметику и низшую алгебру, начальную и высшую геометрию, «свойства трёх сечений конуса и прочее до сего относящееся».
М.И. Мордвинов руководил корпусом с некоторым перерывом – до 1764 и после 1771 гг., когда он вернулся в корпус, будучи «директором от строения государевых дорог». О значении математики в военном деле он писал так:
«Геометрия, получая надлежащее развитие в её практических приложениях, должна иметь своё основание в систематическом изложении евклидовых начал, знание которых каждому, кто только чему-нибудь учиться хочет, нужно…»
Здесь же определялось основополагающее значение арифметики для всей математики: Наука счисления есть основание всем математическим наукам и изъяснять примерами, а потом за нужное почитается обучать счислению литерами, чтобы сделать способными учеников к понятию трудных геометрических доказательств. Нынешние авторы пишут все свои дела алгебраически. Итак, не зная сей науки, ученик ими пользоваться не может».
В 1784 г. был утверждён новый учебный план корпуса, согласно которому учащиеся двух младших возрастов все общеобразовательные предметы по курсу главного народного училища, В старших же классах предметы были расположены следующим образом:
ü в 4 классе изучались арифметика и практическая геометрия.
ü в 5 классе – литерная арифметика (алгебра), геометрия, тригонометрия и смешанная математика,
ü в 6 классе – алгебра, механика и гидравлика.
Мордвинов и Шувалов постоянно заботились о том, чтобы Инженерно-артиллерийский корпус имел хороший состав учителей, прежде всего по чистой и прикладной математике. Это выразилось, в частности, даже в том, что особое внимание было уделено достаточному их вознаграждению. Зарплата определялась важностью предмета и удобством подыскания учителей. В числе лучших учителей Инженерно-артиллерийского корпуса мы находим ученика Ломоносова по академической гимназии и университету, его единомышленника, известного философскими сочинениями, поручика артиллерии Якова Павловича Козельского, незаурядного мыслителя, человека большой эрудиции. Он преподавал математику с 1757 г. сначала в объединенной инженерно-артиллерийской школе, а потом в кадетском корпусе в течение 11 лет.
Яков Павлович Козельский (1729-1784) - русский просветитель, философ-материалист. Козельский родом из среды украинского служилого казачества. С 1744 по 1750 г. учился в Киево-Могилянской академии, окончил класс риторики и постиг основы латины. Не закончив академию, переехал в Санкт-Петербург, где сначала стал учеником академической гимназии при Санкт-Петербургской Академии наук, а с 1752 года - студентом Петербургского академического университета, где изучал философию у И. А. Брауна и математику под руководством Г. В. Рихмана.
Преподавательскую деятельность начал с репетиторства по немецкому, латинскому языкам и математике, затем работал в университетской гимназии, обучая немецкому языку, после чего перешел на военную службу. В это время он большое внимание уделял научной работе и переводам: с 1764 по 1766 гг. написал 9 оригинальных работ и переводов математического, инженерного и философского содержания.
Начиная с начала 1760-х годов Я. П. Козельский преподавал математику и механику в Артиллерийском и Инженерном благородном корпусе. В 1764 г. вышли первые опубликованные учебники Я. П. Козельского — «Арифметические предложения» и «Механические предложения». «Арифметические предложения» состояли из 4 глав:
«О целых числах»;
«О содержании и пропорции чисел»;
«О ломаных числах»;
«О выкладках математических».
Уже само название показывает, что содержание намного шире названия. Так, в четвертой главе изложены правила возведения в степень, извлечения квадратных и кубических корней, действия с логарифмами, приведены некоторые задачи на измерение длин, площадей и объёмов. Методика изложения несколько тяжеловесна и похожа на Вольфову. но чутьё практического инженера, да к тому же ещё и литератора, помогло сделать учебник понятным и доступным для учащихся.
После ухода Козельского в АИИК преподавали Н.В. Верещагин и Е.Д. Войтяховский.
Николай Васильевич Верещагин (1744-1807)(не путать с Н.В. Верещагиным (1839-1907), братом художника Верещагина, создателем вологодского масла) - сын вологодского подпоручика пешком добрался до С.-Петербурга и поступил в артиллерийскую школу, преобразованную в 1762 г. в инженерно-артиллерийский корпус, после окончания которого он, как талантливый выпускник был оставлен при корпусе для преподавания чистой и прикладной математики и военных наук.
Н.В. Верещагин стал известным и широко образованным русским математиком-педагогом второй половины XVIII века. Он обладал широчайшей эрудицией: кроме обширных знаний в математических и военных дисциплинах был чрезвычайно сведущ в естествознании, философии и истории, владел французским, немецким, итальянским и латинским языками. Это давало ему возможность следить за развитием математики как науки и отражать в своих лекциях ее новейшие достижения.
Императрица Екатерина II однажды целых два часа слушала его лекцию по механике (за что пожаловала ему 1000 душ крестьян). С 1793 г. Верещагин преподавал военные и математические науки Великим Князьям Александру и Константину Павловичам. Павел I произвел в чин генерал-майора и наградил орденом св. Анны I степени.
По мнению историка математики В.Е Прудникова, это был один из наиболее образованных и культурных преподавателей корпуса: «Он знакомил своих учеников с «Введением в анализ бесконечно малых» Эйлера, показывая им, между прочим, как пользоваться известными подстановками Эйлера при преобразовании квадратных трёхчленов к рациональному виду, и обобщал эти преобразования на корни более сложного вида. Знакомил также с решением систем уравнений 1 степени с 2, 3, 4 и т.д. неизвестными при помощи определителей и с многими другими новинками математической науки того времени… Н.В. Верещагин одним из первых в России начал преподавать аналитическую геометрию».
Труды Верещагина по математике в 3-х томах «Математические предложения о употреблении алгебры во всех частях прямолинейной геометрии, логарифмах, тригонометрии плоской и сферической: [в 3-х т.]. / Сочиненные артиллерии генерал-майором Николаем Васильевичем Верещагиным, найденные после смерти его» были изданы сыном Верещагина в Петербурге в 1819-1820 гг.
Н.В. Верещагин остался в истории математического образования примером бескорыстного служения делу: «Любовь к науке всегда заставляла Верещагина забывать собственные выгоды: для тех воспитанников, которые имели склонность к математике, и для всех любителей этой науки он открыл у себя в доме безденежное чтение лекций».
Итак, Н.В. Верещагин оказал существенное влияние не только на преподавание математики в Инженерно-артиллерийском корпусе, но и на все развитие математического образования во второй половине XVIII в.
Содержание лекций Н.В. Верещагина, по-видимому, легло в основу учебника математики Войтяховского, который был учителем Инженерно-артиллерийского корпуса, а затем руководителем известной в Москве частной «Математической школы». Ефим Дмитриевич Войтяховский - математик-педагог, 22 года служил в артиллерии, преподаватель математических наук, автор учебников 1812-22 гг.
В 1787-90 гг. он издал под длинным и пышным названием «Теоретический и практический курс чистой математики, содержащий в себе Арифметику, Геометрию, Тригонометрию с практикою с описанием пропорционального циркуля или сектора, Алгебру с высшими ступеньками, Криволинейную геометрию с теориею и практикою искусства бросания бомб в пользу и употребление юношества и упражняющимся в математике». Учебник содержал 4 тома и был опубликован в Москве. Несмотря на щекотливые обстоятельства, связанные с появлением книги, она пользовалась популярностью. Благодаря полноте содержания, удачному расположению материала, вполне достаточному количеству практических задач "Курс чистой математики..." около 40 лет был одним из самых распространенных учебных математических пособий для русской средней школы. Система изложения теоретического материала в нем обнаруживает сильное влияние методических идей Хр. Вольфа.
Следует отметить, что несомненный авторитет в образованном русском обществе на самом деле заслужил и весь прекрасно подобранный преподавательский состав Инженерно-артиллерийского корпуса. Сохранилась лестная его характеристика:
«Корпусные учители и офицеры, с самого основания корпуса составляли между собой тесный, дружеский кружок людей, которые вдали от волнения и шума городской жизни с жаром предались науке и чтению, находя в дружеских беседах своего кружка поощрение и помощь в своих занятиях».
Таким образом, Инженерно-артиллерийский кадетский корпус, благодаря умелому руководству и квалифицированным преподавателям, особенно математикам, к концу XVIII в. стал одной из лучших военно-технических школ.
Итак, военные и инженерные учебные заведения сыграли в XVIII веке значительную роль в развитии русского математического просвещения. В конце века в россии уже были свои математики (учёные и преподаватели), самостоятельная русская математическая учебная и научная литература.
Интересно (о Крафте). После успешного проведения экспедиции, по возвращении в Петербург, Крафт попытался вести самостоятельные наблюдения в Академической обсерватории, но из-за противодействия С. Я. Румовского ему в этом было отказано. Тогда Крафт попросил выделить ему средства на создание собственной домашней обсерватории, и, поскольку Академия в этом отказала, он построил ее на собственные средства в 1771 г. Обсерватория находилась на чердаке над квартирой Крафта. Наблюдения велись через отверстие в кровле. «Моменты контактов при схождении и расхождении дисков Солнца и Луны определялись с точностью до долей секунды». Известно, что Крафт наблюдал в своей обсерватории затмение Солнца, происшедшее 12 марта 1773 г.
Интересно о БарсовеОстается загадкой, как могло случиться, что восьмилетнего ребенка приняли в Славяно-греко-латинскую академию. Дело в том, что в указе Синода сказано, что в академию могут быть приняты ученики в возрасте от 13 до 20 лет. Когда в 1737 г. из присланных в академию дворянских детей 73 человека оказались моложе 12 лет, по указу императрицы их отправили обратно, пообещав принять позже, по достижении ими двенадцати лет.
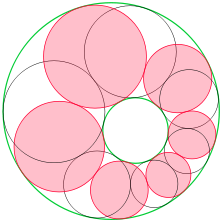
Дополнения. В 1822 году французский математик и механик Жан Виктор Понселе опубликовал «Трактат о проективных свойствах фигур», где сформулировал теорему о замкнутых ломаных, вписанных в одну окружность и описанных около другой. С этого началась история одной из красивейших теорем планиметрии — теоремы Понселе. Её многократно усиливали и обобщали. Появились и теоремы «в духе Понселе» — так называемые теоремы о замыкании; например, поризм Штейнера (аналог теоремы Понселе для цепочки окружностей, касающихся двух данных окружностей) и «теорема о зигзаге» (иногда называемая «теоремой о блохе»). Интерес к теоремам о замыкании не ослабел и сегодня: за последние годы им было посвящено несколько десятков математических статей.
1) Поризм Штейнера: Рассмотрим цепочку окружностей 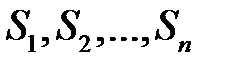 , каждая из которых касается двух соседних (
, каждая из которых касается двух соседних ( 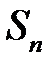 касается
касается 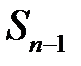 и
и 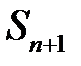 ) и двух данных непересекающихся окружностей
) и двух данных непересекающихся окружностей 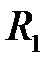 и
и 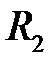 . Тогда для любой окружности
. Тогда для любой окружности 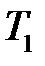 , касающейся
, касающейся 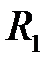 и
и 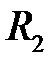 (одинаковым образом, если
(одинаковым образом, если 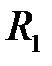 и
и 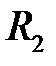 не лежат одна в другой, внешним и внутренним образом — в противном случае), существует аналогичная цепочка из касающихся окружностей
не лежат одна в другой, внешним и внутренним образом — в противном случае), существует аналогичная цепочка из касающихся окружностей 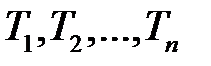 .
.
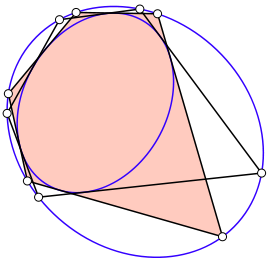
Цепь Понселе: Пусть 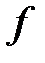 и
и 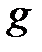 — два конических сечения. Ломаная
— два конических сечения. Ломаная 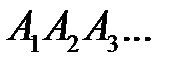 называется цепью Понселе для пары
называется цепью Понселе для пары 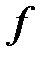 ,
, 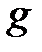 , если каждая вершина
, если каждая вершина 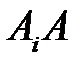 лежит на
лежит на 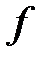 и при этом (продолжения) рёбер
и при этом (продолжения) рёбер 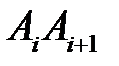 и
и 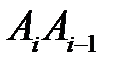 являются соответственно правой и левой касательной к
являются соответственно правой и левой касательной к 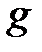 .
.
Поризм Понселе: Если одна цепь Понселе пары 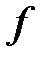 и
и 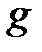 зацикливается за
зацикливается за 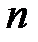 шагов (то есть
шагов (то есть 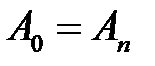 ), то и любая цепь Понселе пары
), то и любая цепь Понселе пары 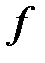 и
и 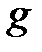 зацикливается за
зацикливается за 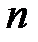 шагов.
шагов.
2) Полигонометрия (от греч. polýgonos - многоугольный и …метрия) - один из методов определения взаимного положения точек земной поверхности для построения опорной геодезической сети, служащей основой топографических съёмок, планировки и строительства городов, перенесения проектов инженерных сооружений в натуру и т. п. Положения пунктов в принятой системе координат определяют путём измерения на местности длин линий, последовательно соединяющих эти пункты и образующих полигонометрический ход, и горизонтальных углов между ними. Пункты полигонометрии закрепляются на местности закладкой геодезических центров в виде подземных бетонных монолитов или металлических труб с якорями и установкой геодезических сигналов (наземных знаков в виде деревянных или металлических пирамид).
Дата добавления: 2016-06-05; просмотров: 2455;











