Простые комплексно-сопряженные корни.
При решении характеристического уравнения системы могут получиться не только действительные, но и комплексные корни, которые будут попарно сопряжены (что следует из основной теоремы алгебры: при решении алгебраического уравнения n-го порядка c действительными коэффициентами комплексные корни всегда попарно сопряжены).
Пусть есть корни характеристического уравнения : 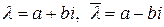 кратности 1, то есть два простых комплексно-сопряженных корня. Можно доказать, что значения собственных векторов будут тоже комплексно сопряжены:
кратности 1, то есть два простых комплексно-сопряженных корня. Можно доказать, что значения собственных векторов будут тоже комплексно сопряжены: 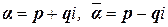 , а также, частные комплекснозначные решения из ФСР, соответствующие данным собственным значениям, будут тоже комплексно сопряжены:
, а также, частные комплекснозначные решения из ФСР, соответствующие данным собственным значениям, будут тоже комплексно сопряжены:
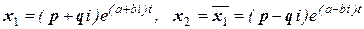 .
.
В качестве действительных решений в ФСР, соответствующих комплексно сопряженным решениям, можно взять их линейные комбинации:
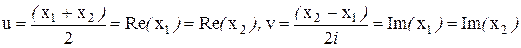 .
.
Можно показать, что эти решения будут линейно независимы.
Итак, для получения действительных решений из ФСР, необходимо найти одно комплекснозначное решение, выделить в нем действительную и мнимые части и принять за 2 действительных решения в ФСР, соответствующих двум комплексно сопряженным корням характеристического уравнения, вектор-функции u и v.
Пример 5.3.Решим систему
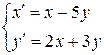 .
.
Матрица системы 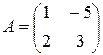 . Характеристическое уравнение:
. Характеристическое уравнение: 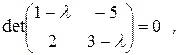
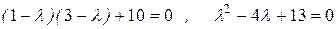 .
.
Корни характеристического уравнения: 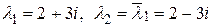 .
.
Находим собственный вектор, соответствующий 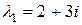 :
:
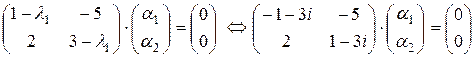 .
.
Покажем, что строки матрицы системы пропорциональны:
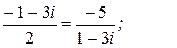 так как
так как 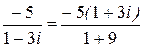 .
.
Отсюда, приняв за свободную переменную 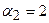 получим
получим 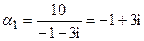 и
и 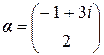 .
.
Частное решение, соответствующее данному собственному числу матрицы:
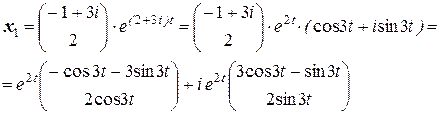
Частные решения из ФСР имеют вид
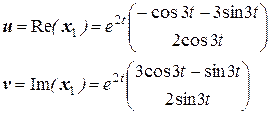 .
.
Общее решение в векторной форме:
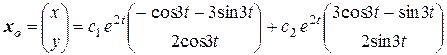 .
.
Общее решение в координатной форме:
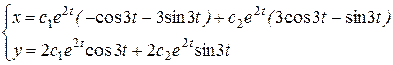
5.5. Однородная система ЛДУ с постоянными коэффициентами. Случаи простых и кратных корней характеристического уравнения. Понятия жордановой формы матрицы, матричной экспоненты и их вычисление. Метод решения системы с помощью вычисления матричной экспоненты.
Случаи кратных корней характеристического уравнения более рационально рассмотреть, используя метод решения системы с помощью матричной экспоненты. Для этого потребуется вспомнить некоторые понятия линейной алгебры. Но прежде рассмотрим случай действительных кратных корней, когда количество собственных векторов, соответствующих кратному корню характеристического уравнения, равно его кратности. В этом случае построение ФСР проводится аналогично случаю простых действительных корней.
Пример 5.4.Решим систему
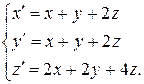
Матрица системы 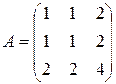 . Характеристическое уравнение:
. Характеристическое уравнение:
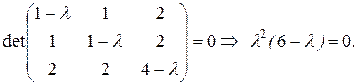
Корни характеристического уравнения: 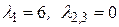 . Находим собственные векторы:
. Находим собственные векторы: 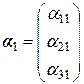 ,
, 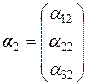 ,
, 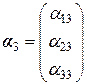 .
.
1. 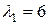
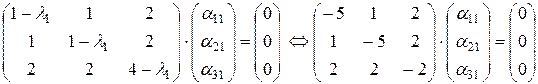
Приведем матрицу системы к ступенчатому виду.
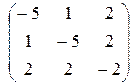 ~
~ 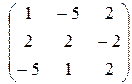 ~
~ 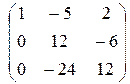 ~
~ 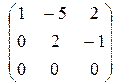
Ранг матрицы равен двум. Количество независимых решений k = n - r = 3 – 2 = 1. Выберем за базисный минор, соответствующий 1-ой и 2-й переменной. Тогда за свободную переменную выберем α31= 2 (выбираем значение, которое даст значения остальных переменных целочисленными). Отсюда получим: α21= 1 , α11= 1 и, соответственно, 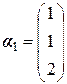 . Частное решение, соответствующее данному собственному числу матрицы:
. Частное решение, соответствующее данному собственному числу матрицы:
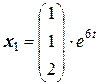
2. 
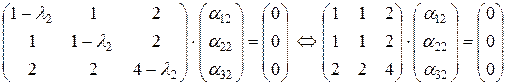
Приведем матрицу системы к ступенчатому виду.
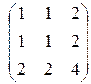 ~
~ 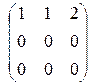
Ранг матрицы равен 1. Количество независимых решений k = n - r = 3 – 1 = 2. Выберем за базисный минор, соответствующий 1-ой переменной. Тогда за свободные переменные выберем α22и α32 . Тогда получим 2 собственных вектора, соответствующих кратному значению собственного числа:
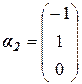 ,
, 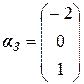 .
.
Соответствующие решения системы ДУ из ФСР совпадают с собственными векторами вследствие равенства 1 множителя е0t:
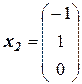 ,
, 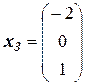 .
.
Общее решение в векторной форме 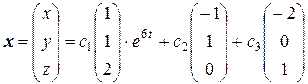 .
.
Или в координатной форме:
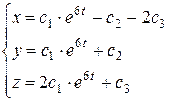
Вернемся теперь к более общему случаю, когда при кратных корнях характеристического уравнения системы число собственных векторов меньше, чем размерность системы ОЛДУ. Будем искать фундаментальную матрицу системы 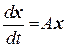 в виде: e Аt. Рациональный путь вычисления матричной экспоненты состоит в следующем.
в виде: e Аt. Рациональный путь вычисления матричной экспоненты состоит в следующем.
Если привести матрицу системы А к жордановой форме путем преобразования:
В = С -1 А С, где С - матрица перехода к жордановой форме, далее вычислить матричную экспоненту e Вt от матрицы системы в жордановой форме, (что относительно просто сделать из определения), а затем матричную экспоненту перевести в старый базис при помощи преобразования e Аt = Сe Bt С -1, то получим фундаментальную матрицу e Аt, столбцы которой представляют решения из ФСР исходной системы ОЛДУ. Итак, рассмотрим подробнее намеченный план действий.
1. Приведение матрицы системы к жордановой форме.
Напомним из курса линейной алгебры, что если каждому собственному числу квадратной матрицы А, определяемому как корень характеристического уравнения матрицы:
det(A-λE) = 0, соответствует ровно столько собственных векторов, какова кратность этого корня (то есть собственного числа λ), то матрицу можно привести к диагональному виду преобразованием: D = U -1AU, где D - диагональная матрица, у которой по главной диагонали стоят собственные числа, остальные элементы матрицы равны нулю, A – исходная матрица, U – матрица перехода в базис из собственных векторов, столбцы которой есть собственные векторы матрицы, U -1 – матрица, обратная к матрице перехода.
Если же число собственных векторов матрицы А меньше размерности матрицы, то любую квадратную матрицу можно привести к жордановой форме преобразованием: В = С -1AС, где A – исходная матрица, С – матрица перехода, столбцы которой есть собственные векторы матрицы и присоединенные к ним, С -1 – матрица, обратная к матрице перехода, В – матрица, имеющая жорданову форму, а именно:
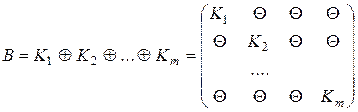 .
.
Матрица В состоит из прямой суммы жордановых клеток Ki , блоки Θ – нулевые матрицы соответствующей размерности. Если кратность собственного числа равна 1, то соответствующая жорданова клетка имеет размерность 1х1, т.е. представляет собой один элемент, равный соответствующему собственному числу λj. Если λi – кратный действительный корень, для которого количество собственных векторов меньше кратности корня, то жорданова клетка имеет вид:
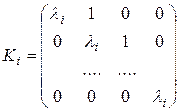 ,
,
то есть по диагонали стоит значение λi , над главной диагональю единицы, остальные нули. Размерность жордановой клетки соответствует кратности рассматриваемого корня. Осталось напомнить, что присоединенные векторы определяются из соотношений:
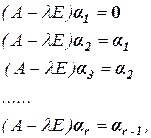 (5.7)
(5.7)
где r – кратность корня λi , α1 – собственный вектор, αi – присоединенные векторы.
Замечание. Если число собственных векторов для некоторого кратного корня λi больше 1, но меньше кратности корня r, то процесс вычисления присоединенных векторов для каждого из собственных векторов определяется теми же соотношениями (5.7). Жорданова клетка, соответствующая этому собственному числу разбивается на m клеток (m - число собственных векторов для λi , m < r). Размерность каждой из m клеток равна количеству присоединенных (к соответствующему собственному) векторов плюс 1. Максимальное количество присоединенных векторов для каждого собственного вектора определится несовместностью соответствующей СЛАУ из соотношений (5.7).
2. Вычисление матричной экспоненты e Bt .
Матричной экспонентой или показательной функцией матрицы А называется сходящийся при любых квадратных матрицах А ряд:
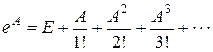 .
.
Можно показать, что для любой квадратной матрицы А и любого t1 > 0, ряд 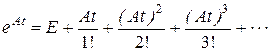 сходится абсолютно и равномерно в круге
сходится абсолютно и равномерно в круге 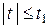 комплексной плоскости (см. [1] гл.3).
комплексной плоскости (см. [1] гл.3).
Напомним сначала свойства матричной экспоненты:
1. Если А = СВС -1, то и e A = Сe B С -1,
2. Если АВ = ВА, то e А + B = e А e B = e B e А ,
3. Если X(t) = e At , то X(t) удовлетворяет системе: 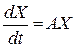 при начальных условиях X(0) = Е, то есть X(t) – фундаментальная матрица системы.
при начальных условиях X(0) = Е, то есть X(t) – фундаментальная матрица системы.
Для любой жордановой клетки: e K t = e (λE+F)t = e λt E e Ft = e λt e Ft , где
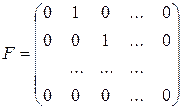 ,
,
так как EF = FE, и el E t = e l tE .
С учетом того, что F r = Θпри любом 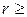 размерности жордановой клетки, e Ft вычисляется легко из определения матричной экспоненты:
размерности жордановой клетки, e Ft вычисляется легко из определения матричной экспоненты: 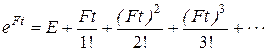 .
.
Получив таким образом матричные экспоненты для каждой жордановой клетки матрицы В, получим прямым суммированием матричную экспоненту от жордановой формы матрицы системы:
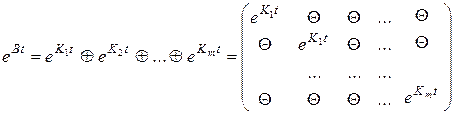 .
.
3. Получение фундаментальной матрицы исходной системы ДУ.
Перейдем в старый базис: e Аt = Сe Bt С -1. Тогда столбцы полученной матрицы составят ФСР исходной системы ОЛДУ. Приведем еще одну теорему, с помощью которой легко отыскать частное решение системы при известных начальных условиях при t = 0.
Теорема 5.4.Задача Коши 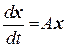 , при начальных условиях
, при начальных условиях 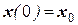 , имеет решение:
, имеет решение: 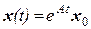 .
.
Доказательство. Подставим это решение в исходную систему. 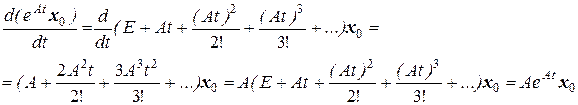
Так как ряд сходится равномерно, то почленное дифференцирования ряда допустимо.
Получили: 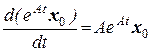 , при этом в точке t = 0
, при этом в точке t = 0 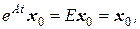 что и требовалось доказать.
что и требовалось доказать.
Пример 5.5. Решим систему ДУ.
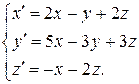
Матрица системы: 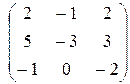 Характеристическое уравнение системы:
Характеристическое уравнение системы:
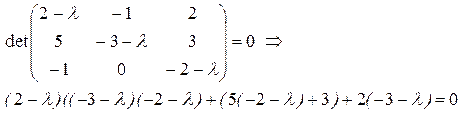
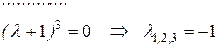
Система уравнений для отыскания собственного вектора 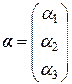 :
:
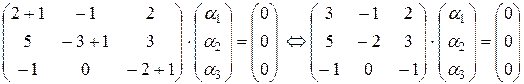
Приведем матрицу системы к ступенчатому виду.
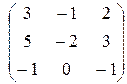 ~
~ 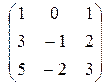 ~
~ 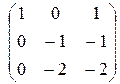 ~
~ 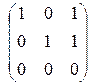
Ранг матрицы равен 2. Число независимых решений k = n - r = 3 – 2 = 1. Выберем за базисные переменные первую и вторую. Тогда свободная переменная третья. Примем ее значение равным 1. Получим собственный вектор: 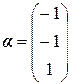 . Для получения присоединенных векторов (обозначим их
. Для получения присоединенных векторов (обозначим их 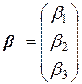 и
и 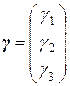 , чтобы не усложнять запись двойными индексами) необходимо решить две неоднородные СЛАУ:
, чтобы не усложнять запись двойными индексами) необходимо решить две неоднородные СЛАУ:
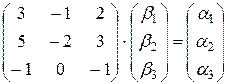 и
и 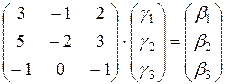 .
.
Решим сначала первую систему, для чего приведем к ступенчатому виду расширенную матрицу.
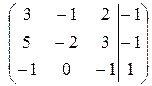 ~
~ 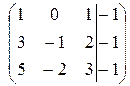 ~
~ 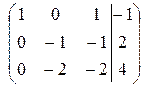 ~
~ 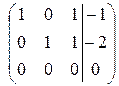
Ранг расширенной матрицы равен рангу матрицы системы и равен двум. Значит, по критерию Кронекера-Капелли система совместна. Число независимых решений k = n - r = 3 – 2 = 1. Пусть базисный минор соответствует первым двум неизвестным, а свободная переменная третья. Тогда из преобразованной системы, соответствующей расширенной матрице ступенчатого вида, получим первый присоединенный вектор: 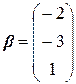 .
.
Для второй системы аналогично получим:
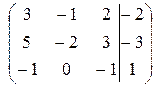 ~
~ 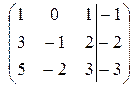 ~
~ 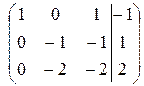 ~
~ 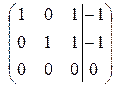
Ранг расширенной матрицы равен рангу матрицы системы и равен двум. Число независимых решений k = n - r = 3 – 2 = 1. Пусть базисный минор соответствует первым двум неизвестным, а свободная переменная третья. Тогда получим второй присоединенный вектор: 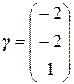 .
.
Матрица перехода к жордановой форме, составленная из собственного и присоединенных векторов, 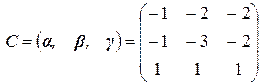 . Найдем матрицу, обратную к ней, методом элементарных преобразований строк.
. Найдем матрицу, обратную к ней, методом элементарных преобразований строк.
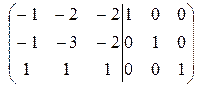 ~
~ 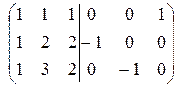 ~
~ 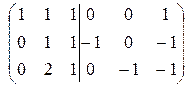 ~
~
~ 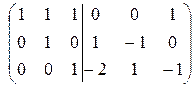 ~
~ 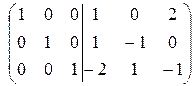
Обратная матрица 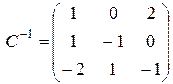 . Отметим, что условие
. Отметим, что условие 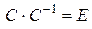 выполняется. Получим жорданову форму матрицы, больше для проверки правильности найденной матрицы перехода, так как вид жордановой формы мы знаем уже заранее:
выполняется. Получим жорданову форму матрицы, больше для проверки правильности найденной матрицы перехода, так как вид жордановой формы мы знаем уже заранее:
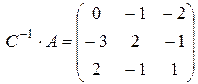 и
и 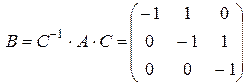 .
.
Далее вычисляем матричную экспоненту.
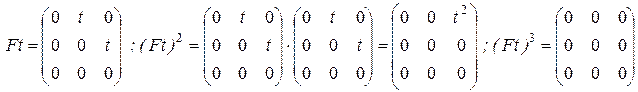
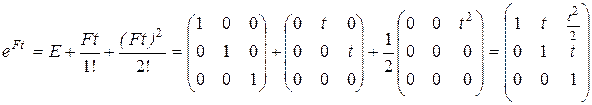
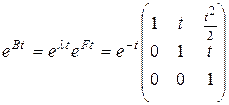
Вычислим фундаментальную матрицу: 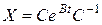
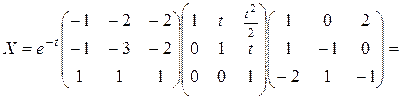
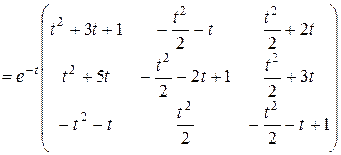
Ответ в координатной форме:
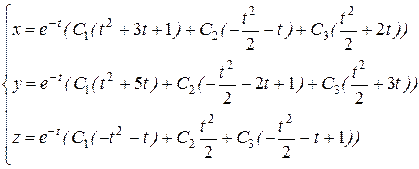
Пример 5.6. Решим систему ДУ
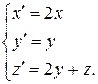
Это система легко разрешается и без указанных методов. Так, интегрируя первое уравнение, получаем: 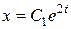 . Интегрируя второе уравнение, получаем:
. Интегрируя второе уравнение, получаем: 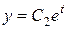 . Тогда последнее уравнение является линейным неоднородным, первого порядка. Методом вариации постоянной находим
. Тогда последнее уравнение является линейным неоднородным, первого порядка. Методом вариации постоянной находим 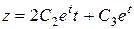 .
.
Покажем теперь на этом примере, как работает метод решения, основанный на вычислении матричной экспоненты.
Матрица системы имеет вид: 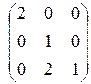 . Характеристическое уравнение системы:
. Характеристическое уравнение системы:
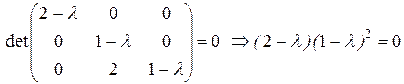
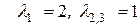
Для 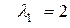 :
:
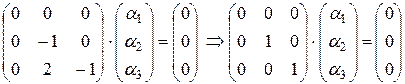
Ранг матрицы равен 2. Число независимых решений k = n - r = 3 – 2 = 1.
Выберем за базисные переменные третью и вторую. Тогда свободная переменная первая. Примем ее значение равным 1. Получим собственный вектор
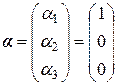 .
.
Для 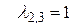 :
:
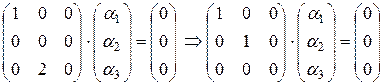
Ранг матрицы равен 2. Число независимых решений k = n - r = 3 – 2 = 1.
Выберем за базисные переменные первую и вторую. Тогда свободная переменная третья. Примем ее значение равным 1. Получим собственный вектор
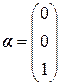 .
.
Для получения присоединенного вектора необходимо решить неоднородную СЛАУ:
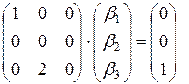 .
.
Приведем к ступенчатому виду расширенную матрицу.
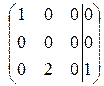 ~
~ 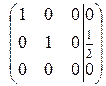
Ранг расширенной матрицы равен рангу матрицы системы и равен двум. Значит, по критерию Кронекера-Капелли система совместна. k = n - r = 3 – 2 = 1. Следовательно, решений бесконечно много. Для отыскания произвольного частного решения неоднородной СЛАУ в этом случае достаточно принять свободную переменную (в нашем примере это 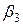 ) за 0. Получим присоединенный вектор:
) за 0. Получим присоединенный вектор:
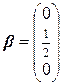 .Матрица перехода
.Матрица перехода 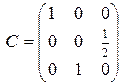 , обратная к ней
, обратная к ней 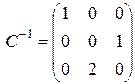 .
.
Отсюда жорданова форма матрицы А:
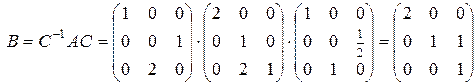 .
.
Вычислим e Ft для жордановой клетки, соответствующей корню 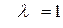 .
.
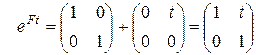 , (Ft)2 = Q.
, (Ft)2 = Q. 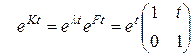
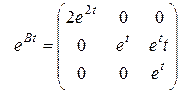
Отсюда: 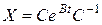
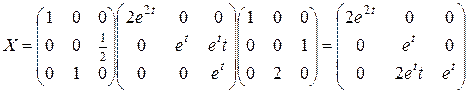
Получаем ответ в координатной форме:
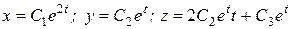
5.6. Неоднородная система ЛДУ. Метод решения – метод вариации произвольных постоянных (метод Лагранжа).
Метод Лагранжа решения систем НЛДУ вида (5.3) заключается в следующем:
- сначала решаем соответствующую систему ОЛДУ, получаем для нее общее решение,
- далее предполагаем, что общее решение исходной системы НЛДУ имеет такой же вид, но вместо произвольных констант в решении стоят некоторые функции независимого аргумента,
- эти неизвестные функции определяем при решении системы уравнений вида:
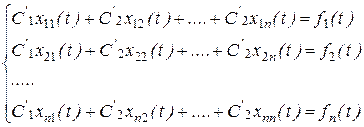 (5.8)
(5.8)
Где столбцы хj=(x1j, x2j,…, xnj)Тсоставляют ФСР системы ОЛДУ. Эта система уравнений относительно производных неизвестных функций Сi (t) имеет определитель, равный определителю Вронского, никогда не обращающегося в нуль (в области существования решений), а, следовательно, решение в виде вектор-функции С'=(С'1(t), С'2(t),…, С'n(t))тсуществует и оно единственно.
Подробности вывода системы (5.8) см. [1], глава 3.
Пример 5.7.Решим систему
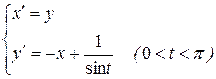
Решаем сначала соответствующую систему ОЛДУ.
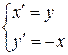
Матрица системы А= 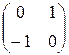 и, соответственно, характеристическое уравнение имеет вид:
и, соответственно, характеристическое уравнение имеет вид: 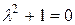 . Откуда
. Откуда 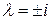 и собственные векторы матрицы:
и собственные векторы матрицы: 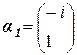 и
и 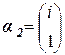
Комплекснозначные решения системы, составляющие ФСР, имеют вид:
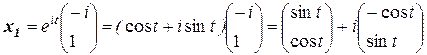 и
и
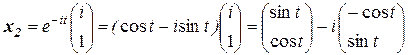
Возьмем в качестве действительных решений действительную и мнимую часть комплекснозначных решений. Тогда общее решение системы ОЛДУ примет вид:
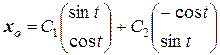
Составим систему (5.8) для отыскания неизвестных функций С1(t)и C2(t).
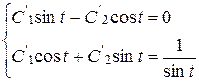
Из первого уравнения имеем 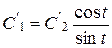 . Подставив выражение во второе уравнение, получим
. Подставив выражение во второе уравнение, получим 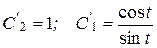 . Отсюда
. Отсюда 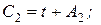
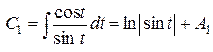 , где А1 и А2– произвольные константы. Тогда общее решение исходной системы НЛДУ после несложных преобразований примет вид:
, где А1 и А2– произвольные константы. Тогда общее решение исходной системы НЛДУ после несложных преобразований примет вид:
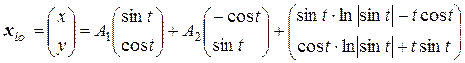
Дата добавления: 2021-05-28; просмотров: 223;