Взаимно простые числа
Определение 5.1. Целые числа 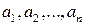 называются взаимно простыми, если их НОД равен
называются взаимно простыми, если их НОД равен 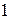 :
:
Примеры.
1. Числа 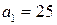 и
и 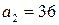 – взаимно простые.
– взаимно простые.
2. Числа 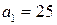 и
и 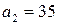 – не взаимно простые, так как
– не взаимно простые, так как 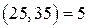 .
.
Следующая теорема устанавливает необходимое и достаточное условие взаимной простоты чисел.
Теорема 5.1 (признак взаимной простоты чисел). Для того, чтобы числа  и
и  были взаимно простыми, необходимо и достаточно, чтобы нашлись такие целые числа
были взаимно простыми, необходимо и достаточно, чтобы нашлись такие целые числа 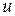 и
и 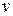 , что
, что 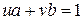 .
.
Доказательство. 1. Необходимость. Пусть числа  и
и  взаимно просты, то есть
взаимно просты, то есть 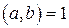 . Тогда по теореме о линейном представлении НОД найдутся такие целые числа
. Тогда по теореме о линейном представлении НОД найдутся такие целые числа 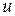 и
и 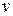 , что
, что 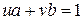 .
.
2. Достаточность. Пусть справедливо утверждение 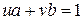 , где
, где 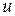 и
и 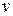 – целые числа. Докажем, что
– целые числа. Докажем, что 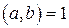 . Предположим, что числа
. Предположим, что числа  и
и  не являются взаимно простыми:
не являются взаимно простыми: 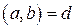 , причем
, причем 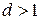 . Тогда
. Тогда 

 и
и 

 , и по свойству делимости
, и по свойству делимости 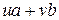

 . Значит,
. Значит, 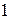

 , следовательно,
, следовательно, 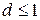 . Полученное противоречие доказывает, что сделанное нами предположение неверно, и, тем самым, справедливо
. Полученное противоречие доказывает, что сделанное нами предположение неверно, и, тем самым, справедливо 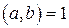 .
.
Следствие 1. Если числа  и
и  взаимно просты, причем
взаимно просты, причем 

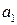 и
и 

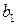 , то числа
, то числа 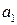 и
и 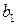 также взаимно просты.
также взаимно просты.
Доказательство. По теореме из взаимной простоты чисел  и
и  следует, что найдутся такие целые числа
следует, что найдутся такие целые числа 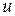 и
и 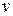 , что
, что 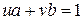 . Из определения делимости
. Из определения делимости 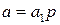 ,
, 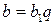 , где
, где 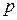 и
и 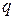 – целые числа. Тогда
– целые числа. Тогда
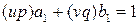 , а, значит, числа
, а, значит, числа 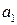 и
и 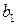 взаимно просты.
взаимно просты.
Следствие 2. Рассмотрим целые числа  ,
,  и
и  . Если
. Если 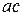

 и
и 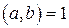 , то
, то 

 .
.
Доказательство. По теореме условие 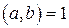 можно записать в
можно записать в
следующем виде: 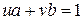 , где
, где 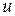 и
и 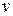 – целые числа. По определению делимости условие
– целые числа. По определению делимости условие 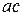

 означает, что найдется такое целое число
означает, что найдется такое целое число 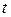 , что
, что 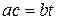 . Умножим обе части последнего равенства на
. Умножим обе части последнего равенства на 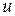 , получим
, получим 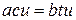 . Но
. Но 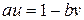 , тогда
, тогда
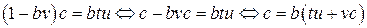 .
.
Поскольку 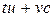 – целое число, последнее равенство означает, что
– целое число, последнее равенство означает, что 

 .
.
Дата добавления: 2021-02-19; просмотров: 650;











