Понятия нормальной, автономной систем, систем ЛДУ (однородных и неоднородных).

Сведение уравнения n-го порядка, разрешенного относительно старшей производной, к нормальной системе.

Система дифференциальных уравнений первого порядка, разрешенных относительно первой производной, вида

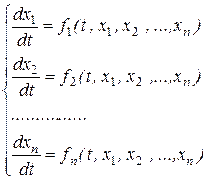(5.1)

называется нормальной системой ДУ.

Если правые части уравнений в (5.1) в явном виде не зависят от аргумента, то такая система ДУ называется автономной. Автономная система имеет вид

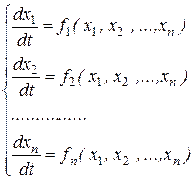. (5.2)

Предполагается, что неизвестные функции x_i зависят от аргумента t.

Порядок нормальных систем определяется количеством неизвестных функций (или таким же количеством уравнений).

Решением системы ДУ называется вектор-функция х = (х₁(t), х₂(t), …, х_n(t))^т, которая при подстановке в исходную систему ДУ даст систему тождеств.

Наиболее изученными и имеющими аналитические решения являются нормальные системы линейных ДУ. Линейные системы ДУ имеют вид

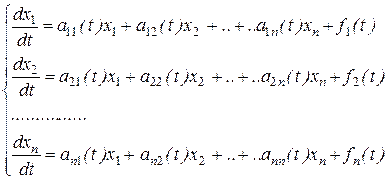(5.3)

Линейная система (5.3), имеющая ненулевые функции в правой части 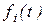(i =1, …, n), называется неоднородной линейной системой ДУ (система НЛДУ).

Если же все 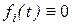(i =1, …, n), то есть система имеет вид

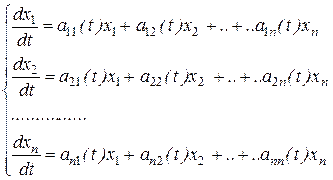, (5.4)

то такая система называется однородной линейной системой ДУ (система ОЛДУ).

Векторные формы записи систем (5.3) и (5.4) имеют, соответственно, вид 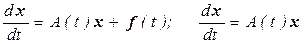, где векторы х = (х₁(t), х₂(t), …, х_n(t))^т,
f(t) = (f₁(t), f₂(t),……, f_n(t))^Т, а матрица

.

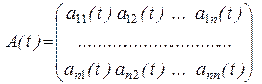Любое ДУ n-го порядка, разрешенное относительно старшей производной, вида

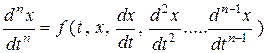(5.5)

можно свести к нормальной системе ДУ вида (5.1). Покажем это. Введем n функций следующим образом:

y₁ = x, y₂ = 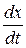, y₃ = 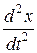, …, y_n = .

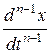Отсюда получим нормальную систему вида (5.1)

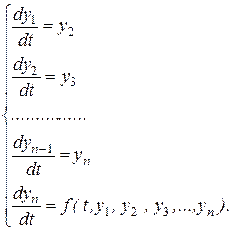
5.2. Системы второго порядка. Метод решения путем сведения к уравнению 2-го порядка.

Рассмотрим сначала нормальную систему ДУ второго порядка, которую можно свести к дифференциальному уравнению 2-го порядка. Пусть есть система вида

.

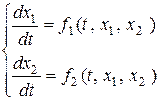Выразим из любого уравнения ту неизвестную функцию, производной которой в этом уравнении нет (например, из первого уравнения х₂ или из второго уравнения х₁). Вычислим производную этой функции и подставим полученные выражения для рассматриваемой функции и ее производной в оставшееся уравнение системы. Таким образом получим уравнение второго порядка относительно одной неизвестной функции, разрешив которое, можно получить решение относительно второй неизвестной функции.

Пример 5.1.Решим систему

.

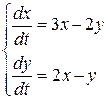Выразим функцию х из второго уравнения: 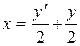. Продифференцируем его: 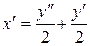. Подставим полученные выражения в первое уравнение системы: 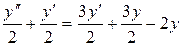. Приведя подобные члены, придем к ОЛДУ второго порядка с постоянными коэффициентами: 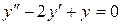. Характеристическое уравнение смситемы: 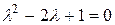. Это уравнение имеет корень 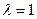кратности 2. ФСР: 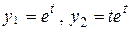. Общее решение для неизвестной функции : .

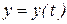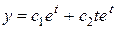Продифференцировав, получим: 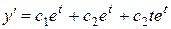. Отсюда общее решение функции для неизвестной функции : .

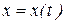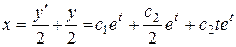Ответ: .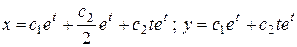

5.3. Системы ОЛДУ и НЛДУ. Теоремы о структуре общего решения (формулировки). Понятие задачи Коши для систем. Формулировка теоремы о существовании и единственности решения.

Фундаментальной системой решений (ФСР) для системы ОЛДУ n-го порядка называется любая система n линейно независимых вектор-функций:
х_i(t) = (х_1i(t), х_2i (t), …, х_ni (t))^т (i = 1, …, n), являющихся решениями системы ОЛДУ.

Фундаментальной матрицей системы называется матрица, составленная из ФСР:

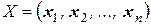
Определитель фундаментальной матрицы называется определителем Вронского … 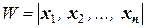, который в силу независимости решений из ФСР не равен 0 ни в одной точке области существования решений системы.

Теорема 5.1 (о структуре общего решения системы ОЛДУ).

Пусть вектор-функции х_i(t) = (х_1i(t), х_2i (t), …, х_ni (t))^т (i = 1, 2,…, n) составляют ФСР системы ОЛДУ n-го порядка 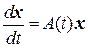. Тогда общее решение системы будет иметь вид x_o(t) = c₁x₁(t) + c₂x₂(t) + …. +c_nx_n(t), где c₁, c₂, …..c_n – произвольные постоянные.

Доказательство теоремы см. в [1] или [2].

Теорема 5.2(о структуре общего решения системы НЛДУ).

Общее решение системы НЛДУ n-го порядка 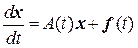имеет вид

x_нo(t) = x_o(t) +x_ч(t),

где x_o(t) = c₁x₁(t) + c₂x₂(t) + …. +c_nx_n(t) – общее решение соответствующей системы ОЛДУ, а x_ч(t)– частное решение системы НЛДУ.

Доказательство теоремы см. в [1] или [2].

Решить задачу Коши для системы ДУ – найти такое единственное решение системы, которое удовлетворяет начальным условиям задачи Коши вида

х_i( t₀) = x_i0 (i = 1, …, n), (5.5)

(где t₀– заданное значение аргумента, x_i0 – числовые значения неизвестных скалярных функций в точке t₀ )_, то есть найти конкретные числовые значения c_i (i = 1, …, n) - произвольных постоянных, входящих в общее решение системы.

В векторной форме начальные условия задачи Коши имеют вид:

x(t₀) = x₀ , где х₀ = (х₁₀, х₂₀, …, х_n0 )^Т.

Теорема 5.3 (теорема Коши о существовании и единственности решения для систем ДУ).

Пусть для нормальной системы ДУ вида (5.1) выполняются следующие условия:

1. Функции 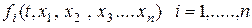, стоящие в правых частях уравнений, определены и непрерывны в некоторой ограниченной замкнутой (n+1)-мерной области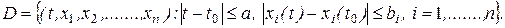

2. В D определены и непрерывны все частные производные этих функций

.

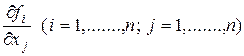Тогда на некотором отрезке [t₀-h, t₀+h], 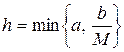, где 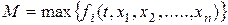в области D, существует единственное решение системы, удовлетворяющее начальным условиям задачи Коши вида (5.5).

Замечание 1.

Из второго условия теоремы следует, что для 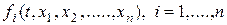выполняется условие Липшица на D, а именно,в D выполняются неравенства 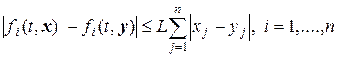, где х и у – векторы, состоящие из значений неизвестных функций в двух разных точках области D при одном значение аргумента t, а L – положительная ограниченная константа, называемая постоянной Липшица (см. [2]). Теорема 5.3 может быть доказана и в том случае, когда вместо условия 2 выполнено условие Липшица. Заметим при этом, что условие Липшица слабее условия непрерывной дифференцируемости правых частей 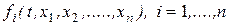по х_i. Действительно, при непрерывной дифференцируемости условие Липшица просто следует из теоремы Лагранжа. Однако, можно привести примеры функций, удовлетворяющий условию Липшица, но не обладающих непрерывной производной.

Замечание 2.

Область, в которой существует единственное решение задачи Коши, есть окрестность точки (t₀, x₀), которая может совпадать с областью D или быть включена в область D. Для более четкого представления об излагаемом здесь материале советуем обратиться к [2], к теореме о существовании и единственности решения для ДУ первого порядка.

Замечание 3.

В случае линейных систем ДУ (5.3) условия теоремы Коши выполняются при условии непрерывности на некотором промежутке 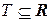функций:

a_{i j} (t), f_i(t),(i=1,…,n; j=1,…,n, ).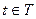

Для систем ОЛДУ вида (5.4) при условии того, что функции a_{i j} (t) представляют собой константы (система ОЛДУ с постоянными коэффициентами), условия теоремы Коши выполняются на всей числовой оси по переменной t.

5.4. Однородная система ЛДУ с постоянными коэффициентами. Построение ФСР в зависимости от корней характеристического уравнения (случаи простых корней).

Система ОЛДУ с постоянными коэффициентами имеет вид:

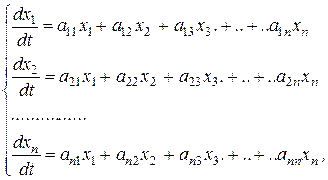(5.6)

где 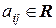- числовые константы.

Или в векторной форме записи: 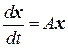. Для такой системы решение задачи Коши существует на всей числовой оси. Частные решения будем искать в виде: 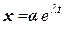, где λ – некоторое число, а α = (α₁, α₂,…, α_n)^Т – вектор, координаты которого есть числа. Для того чтобы подобная вектор-функция была решением системы (5.6) необходимо, чтобы выполнялись следующие условия:

1. (A-λE)α =0
(Эта СЛАУ относительно неизвестного вектора α получается при дифференцировании частного решения, приведенного выше, и подстановке его в систему).

2. det(A-λE) = 0

(Это условие вытекает из предыдущего, так как однородная СЛАУ имеет ненулевые решения только при вырожденной матрице).

Условие 2 есть характеристическое уравнение системы, а числа λ – корни характеристического уравнения, так называемые собственные числа матрицы А. Условие 1 – условие для отыскания собственных векторов матрицы А.(Информацию о собственных числах и собственных векторах матрицы можно отыскать в [3], а подробный вывод условий 1 и 2 в [2]).

Для получения общего решения системы ОЛДУ с постоянными коэффициентами (5.6) необходимо построить ФСР. Для этого вначале решается характеристическое уравнение системы (условие 2) и определяются все собственные числа матрицы системы, которые могут быть как действительные, так и комплексно-сопряженные. Далее для каждого собственного числа λ вычисляются собственные векторы (при решении СЛАУ условия 1). Их может оказаться больше, чем 1, но не более, чем кратность данного корня характеристического уравнения. В зависимости от полученных корней этого уравнения (действительные или комплексные, кратные или простые, т.е. имеющие кратность, равную 1), построение ФСР имеет свои особенности. Рассмотрим вначале более простые случаи – случаи простых (некратных) корней характеристического уравнения.