Доверительный интервал для математического ожидания m в случае, когда среднеквадратическое отклонение s теоретического распределения неизвестно

Рассмотрим теперь более распространенный случай – когда не только среднее, но и дисперсия генеральной совокупности неизвестны.

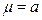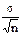Выше было показано, что когда дисперсия известна, выборочное среднее нормально распределено с параметрами и . Мы отнормировали его – вычли из него его математическое ожидание и поделили полученную разность на его среднеквадратическое отклонение. Тем самым перешли от него к стандартной нормальной величине и воспользовались ее свойствами и таблицами.

Заменим в этой операции неизвестное среднеквадратическое отклонение его эмпирической оценкой. Рассмотрим статистику 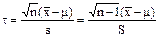(напомним, что s²– несмещенная, а S²– смещенная оценка дисперсии s²).

При нахождении распределения вероятностей для статистики t мы опять должны учесть, что неизвестное математическое ожидание m мы заменили в формулах для s и S на его эмпирический аналог. Можно показать, что t имеет распределение Стьюдента с (n-1) степенями свободы. Это распределение симметрично и при значениях n>20 практически неотличимо от нормального. При меньших n разница заметна и ее надо учитывать. В задачах экономики часто используется распределение Стьюдента с небольшим числом степеней свободы. Для распределения Стьюдента есть многочисленные статистические таблицы. Применив те же рассуждения, что мы применяли при построении доверительного интервала для среднего при известной дисперсии, получаем формулу доверительного интервала для среднего в случае неизвестной дисперсии. А именно, обозначим через t_n,bзначение, для которого

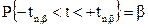, (3.16)

где t имеет распределение Стьюдента с n степенями свободы. Значение t_n,bпо заданному значению b находится по таблицам распределения Стьюдента (см. таблица 6 приложения) аналогично тому, как мы искали k_bдля нормального распределения, используя таблицу 5. При этом надо, правда, еще учесть значение n, что не должно вызвать затруднений. Как правило, таблицы распределения Стьюдента задаются не для всех b, а только для наиболее употребительных значений 0,9, 0,95 и 0,99. Если n велико (больше 20) и под рукой нет таблиц распределения Стьюдента, а имеются только более распространенные таблицы нормального распределения, то можно воспользоваться ими, считая, что с хорошей точностью t_b=k_b. Например, если требуемый уровень доверия 0,95, то можно взять t_n,b=2, а если уровень доверия 0,997, то t_n,b=3 (правило 2s и 3s для нормального распределения).

Итак, для статистики t, имеющей распределение Стьюдента с (n-1) степенью свободы, имеем:

P{|t|<t_n-1,b}=b,

и, проделав простые тождественные преобразования, получаем, что с вероятностью b выполняется

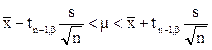. (3.17)

Формула (3.17) – это формула доверительного интервала для математического ожидания m нормального распределения с уровнем доверия b для случая, когда среднеквадратическое отклонение распределения s неизвестно.

Пример . Для проверки фасовочной установки были отобраны и взвешены 20 упаковок. Получены следующие результаты (в граммах).

Найти доверительный интервал для математического ожидания а с надёжностью 0,95, предполагая, что измеряемая величина распределена нормально.

Решение. Находим точечные оценки a и s:

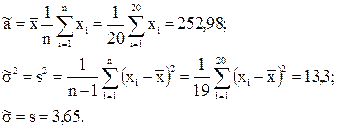
Определяем по таблице 6 распределения Стьюдента для доверительной вероятности b = 0,95 и числа степеней свободы (n - 1) = 19 соответствующее значение t_19,b= 2,093 и по формуле (3.17) находим искомый интервал:

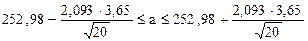или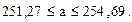

Доверительный интервал для дисперсии

При построении доверительного интервала 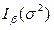для дисперсии пользуются тем, что эмпирическая дисперсия пропорциональна с множителем 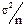величине, имеющей распределение .

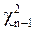Этот доверительный интервал строится по значению s²с помощью таблицы 7 (см. приложение), по формуле

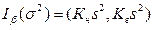, (3.18)

где коэффициенты 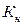и 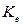соответствуют нижней и верней границе интервала. Они даны в таблице 7 и тем ближе к 1, чем больше n и меньше b. Формулу доверительного интервала для среднего квадратического отклонения s получим из (3.18) с помощью квадратного корня

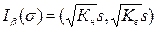. (3.18а)