Последовательность независимых, однородных испытаний. Схема Бернулли

1. Формула Бернулли

Рассмотрим стохастический эксперимент, который, в свою очередь, является последовательностью n независимых и однородных (одинаковых) испытаний, в результате каждого из которых может произойти событие A или ему противоположное 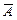с вероятностями p и q = 1 – p, соответственно схема Бернулли. По условию, результат любого испытания не зависит от его порядкового номера и от того, что произошло до него. Простейшим примером может служить многократное бросание монеты, когда с вероятностью p = 0,5 выпадает герб (событие A) и с вероятностью q = 0,5 – решка ( ).

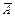Найдём вероятность pn(m) события Bn(m), заключающегося в том, что в результате событие A появится ровно m раз. Очевидно, интересующее нас событие появится тогда, когда появится одно из следующих событий:

.

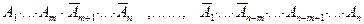Здесь выписаны все комбинации из n сомножителей, из которых m множителей вида A и (n - m) - вида 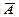, нижний индекс указывает на порядковый номер испытания. Поскольку Bn(m) произойдёт тогда, когда произойдёт или первая, или вторая, ... , или последняя комбинация, то

.

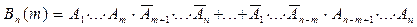В этой сумме имеется всего 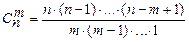(или 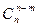) слагаемых. Действительно, для m элементов типа (или n – m элементов типа 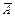) можно выбрать адреса на n позициях n×(n–1)×…×(n–m+1) разными способами. Так как элементы между собой не различаются, то комбинаций на самом деле во столько раз меньше, сколькими способами можно перемешать m элементов между собой, а этих способов m×(m–1)×…×1. Поскольку все слагаемые в этой сумме попарно несовместны, а множители в каждом слагаемом независимы, то искомая вероятность будет равна сумме одинаковых слагаемых, каждое из которых содержит m множителей p(A) = p и n - m множителей p( 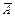) = q. Учитывая, что всего слагаемых 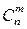, в итоге получим формулу Бернулли

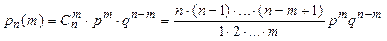. (1.16)

При выводе этой формулы мы попутно показали, что

.

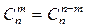Рассмотрим бином Ньютона

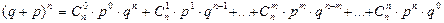. (1.17)

Очевидно, p_n(m) равна соответствующему слагаемому в разложении бинома (здесь для общности мы будем полагать 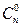и 0! равными единице). Учитывая, что (q + p)ⁿ=1, получим

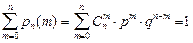. (1.18)

Вероятность события, заключающегося в том, что при n испытаниях A появится не менее m₁раз и не более m₂, вычисляется по формуле

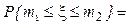
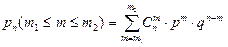. (1.19)

Пример.Вероятность заболевания гриппом во время эпидемии равна 0,4. Найти вероятность того, что из шести сотрудников фирмы заболеет ровно четыре: “заболеет не более четырех” (последнее часто формулируется как “хотя бы (или по крайней мере) две не заболеют”).

Решение. Очевидно, имеет место схема Бернулли, где p = 0,4, q = 1 - p = 0,6, n = 6, m = 4 (m £ 4), поэтому

.

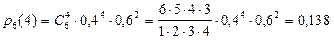На второй вопрос можно найти ответ двумя способами, используя теорему о вероятности противоположного события:

.

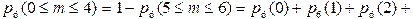
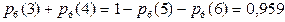Во втором случае вычисления проще, и эту возможность полезно учитывать при решении задач.

1. Асимптотические формулы. Формула Пуассона

Применение формулы Бернулли при больших значениях n приводит к произведению очень больших (n!) и очень малых чисел (p^mи q^{n - m}), что плохо с вычислительной точки зрения, поэтому приходится пользоваться приближенными, асимптотическимиформулами.

При достаточно большом n и малом p (например, n > 100 и a = np < 10) хорошее приближение для формулы Бернулли дает формула

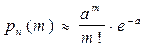. (1.20)

В частности, p_a(0)=e^-a, p_a(1)=ae^-a,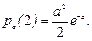

Эта формула задает распределение вероятностей для пуассоновской величины xс параметром a, принимающей целые значения m = 0,1,2,.. с вероятностями 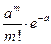. Это распределение имеет самостоятельное значение и ниже мы еще к нему вернемся.

Вероятность события, заключающегося в том, что А появится не более k раз, вычисляется по формуле

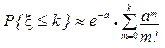. (1.21)

Проведение расчётов облегчается тем, что обе формулы табулированы (таблицы 1 и 2 приложения).

Пример. Известно, при транспортировке и разгрузке керамической отделочной плитки повреждается 2,5%. Найти вероятность того, что в партии из 200 плиток повреждёнными окажется: a) ровно 4; b) не более 6.

Решение. Поскольку вероятность p = 0,025 повреждения плитки мала, n = 200 - велико и
a = np = 5 < 10, можно воспользоваться формулами Пуассона (1.20) и (1.21), применяя Таблицы 1 и 2:

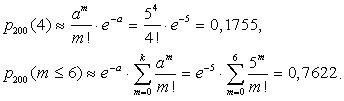
1. Локальная и интегральная формулы Муавра - Лапласа

При достаточно большом n и не слишком малых p и q формула Пуассона уже даёт значительную погрешность и применяется другое приближение - формула Муавра - Лапласа, которую можно получить из формулы Бернулли, совершая предельный переход и применяя формулу Стирлинга для вычисления n!.

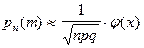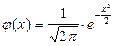, где и 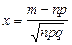. (1.22)

Эта формула также табулирована (таблица 3 приложения), причём, в силу чётности функции 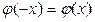, таблица её значений составлена для x ³ 0.

Если при сохранении условий предыдущего пункта нас интересует вероятность того, что при n испытаниях событие A появится не менее m₁и не более m₂раз, то формула (19) с учётом предельного перехода превращается в интегральную формулу Муавра - Лапласа

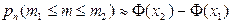, (1.23)

где 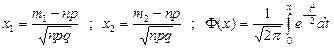и сумма (1.19) превращается в интеграл 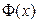.Интеграл 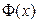называется функцией Лапласа и представляет собой не выражающийся через элементарные функции интеграл. Поскольку функция Лапласа нечетная ( 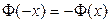) и быстро приближается к своему асимптотическому значению 0,5, то таблица её значений (таблица 4 приложения) составлена для 0 £ x < 5. Для больших значений аргумента с большой точностью можно взять 0,5.

Пример. Вероятность того, что зашедший в ресторан посетитель сделает заказ, равна 0,8. Определить вероятность того, что из 100 зашедших не менее 75 сделают заказ.

Решение. Поскольку n = 100 велико, p = 0,8 и q = 0,2 не малы, применяем интегральную формулу Муавра-Лапласа

.

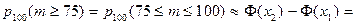
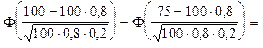
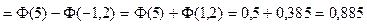Пример. Известно, что 30% призывников имеют 27 размер обуви. Сколько пар обуви надо иметь на складе воинской части, чтобы с вероятностью po= 0,9 были обеспечены все такие призывники, если в часть прибыло 200 новобранцев?

Решение. Очевидно, имеет место схема Бернулли: подбор пары обуви каждому призывнику - одно из 200 испытаний, причём, вероятность того, что ему требуется обувь 27 размера, p = 0,3 (q = 0,7). Пусть на складе имеется k пар обуви, где k пока неизвестно. Требуется подобрать такое k, чтобы 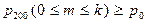. Поскольку n = 200 велико, а p и q не малы, применяем интегральную формулу Муавра-Лапласа

.

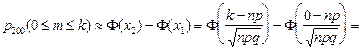
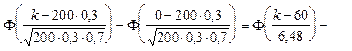
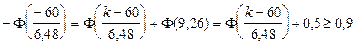Отсюда надо решить неравенство 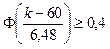. В таблице 4 находим, что F(x)>0,4 при x>1,28, следовательно, (k-60)/6,48>1,28 и k>68,284. То есть на складе достаточно иметь 69 пар обуви такого размера, чтобы с вероятностью 0,9 обеспечить спрос.

1. Распределение Пуассона

Случайная величина, которая принимает значение m с вероятностью ,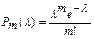
где m = 0,1,2,…, а l - положительная постоянная величина, называется распределенной по Пуассону с параметромl. Закон распределения Пуассона иногда называют законом редких событий (вспомним, что это распределение соответствует схеме Бернулли с маленьким p). Типичная схема, приводящая к закону Пуассона, такова: произойдет или нет событие в интервале времени (t,t+Dt), не зависит от событий, предшествующих моменту t; вероятность отдельного события за малый промежуток времени пропорциональна длине этого промежутка (~lDt); вероятность двух или большего числа событий за малый промежуток времени пренебрежительно мала по сравнению с вероятностью одного события. Эти условия выполняются в большом числе жизненных ситуаций. Примерами пуассоновской величины служит число новорожденных в сутки, число аварий и т.д. Оно широко применяется в теории надежности, в теории массового обслуживания, для него составлены таблицы вероятностей p_mв зависимости от l. Очень важным свойством закона Пуассона и его параметра l является “воспроизводимость”: сумма двух случайных величин, распределенных по Пуассону с параметрами l₁и l₂, распределена также по Пуассону с параметром l₁+l₂; параметр l случайных событий, протекающих во времени и распределенных по Пуассону, пропорционален времени (l - это среднее число событий, наступающих в некоторую единицу времени; роль времени может играть и пространство – например, когда рассматривается число столкновений при полете частиц в пространстве). Это позволяет решать такого рода задачи: известно, что в среднем за год на перекрестке происходит 2 столкновения (число столкновений за год – случайная величина, распределенная по Пуассону с параметром l = 2). Число столкновений за 5 лет распределено по Пуассону с параметром l = 2 × 5 = 10. Или, наоборот, число заявок в месяц распределено по Пуассону, среднее число заявок в месяц – 90, число заявок в день распределено по Пуассону с параметром l = 90/30 = 3.

Ниже приводятся точные рассуждения на эту тему (можно, не изучая точных рассуждений, просто рассмотреть, как решаются подобные задачи).

1. Простейший стационарный (пуассоновский) поток событий

Рассмотрим следующую задачу. Пусть на прямой распределены точки таким образом, что справедливы следующие предположения.

1. На единицу длины в среднем приходится m точек. Последнее не следует понимать так, что на любой единичный отрезок приходится ровно m точек, но если взять достаточно большой по длине отрезок L >> 1 и разделить число точек n, оказавшихся на нём, на его длину, то отношение 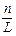при неограниченном увеличении L будет как угодно мало отличаться от m, то есть m играет роль средней плотности.

2. Вероятность расположения того или иного числа точек на отрезке длиной l зависит только от его длины и не зависит от его расположения на прямой.

3. Точки распределяются на прямой независимо друг от друга.

Нас интересует случайная величина 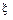число точек, попадающих на отрезок длины 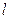. Определим теперь вероятность того, что ровно m точек окажется на отрезке длиной 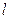. Для этого введём в рассмотрение отрезок длины L, целиком содержащий в себе предыдущий, причём L >> 1. Согласно принятым допущениям на отрезке L расположено 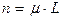точек, причём, каждая из них может оказаться в любом месте отрезка L, и все эти положения равновозможны. Вероятность того, что одна из этих точек окажется на отрезке 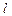согласно справедливой в этом случае геометрической схеме равна 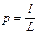и не зависит от того, какая это точка: первая, вторая, ... .

В результате мы пришли к схеме Бернулли (производится n испытаний, в каждом из которых мы следим за одной точкой, и любая из них с вероятностью p может оказаться на отрезке l). Поэтому вероятность того, что ровно m точек из n окажется на отрезке 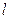, определяется по формуле Бернулли 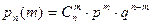, где 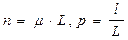. При неограниченном увеличении L (длины отрезка) n стремится к бесконечности, а p - к нулю, но при этом величина 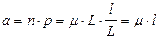остаётся постоянной. Следовательно, можно применять формулу Пуассона, которая в данном случае является точной, а не асимптотической:

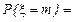
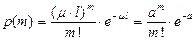. (1.24)

Распределение величины x, определяемое формулой (1.24), называется законом Пуассона.

Если нас интересует вероятность того, что на отрезке l окажется не менее k точек, то применяется формула

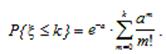(1.25)

Разумеется, вместо отрезка на прямой можно рассматривать плоскость и некоторую её область, трёхмерный случай или, вообще, случай любого числа измерений, а также временной отрезок. В каждом из этих случаев a - среднее число элементов, приходящихся на рассматриваемую область.

Напомним, что формулы (1.24) и (1.25) табулированы (см. таблицы 1,2 приложения).

Пример. Известно, что в среднем за месяц (30 суток) в районной сети водоснабжения возникает 90 ситуаций, требующих оперативного вмешательства аварийной службы. Найти вероятность того, что за одни сутки произойдёт ровно 2 аварии. На сколько вызовов в сутки должна быть рассчитана аварийная служба, чтобы с вероятностью p_o= 0,9 она могла удовлетворить все поступившие за это время заявки?

Решение. Поскольку поток заявок представляет собой простейший, стационарный (пуассоновский) поток событий, то применима формула Пуассона (1.24), где ожидаемое в среднем число заявок в сутки равно ; .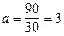

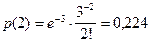Для ответа на второй вопрос задачи предположим, что аварийная служба рассчитана на удовлетворение k заявок в сутки, где k пока неизвестно. Неизвестное k определим из условия 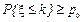, которое принимает вид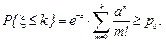

Для определения k пользуемся таблицей 2 значений функции (1.25) при a = 3, подбирая k таким образом, чтобы p(m £ k) оказалась не меньше p_o= 0,9. Найденное таким образом число k = 5, то есть аварийная служба должна быть рассчитана на 5 заявок в сутки.