Понятие о цифровой обработке сигналов. Области применения цифровых фильтров

Цифровую обработку сигналов проводят с целью оценки их пара­метров или преобразования в другую форму средствами вычислительной техники. Достигнутый в настоящее время уровень технологии поз­воляет создавать устройства цифровой обработки сигналов с высокими быстродействием и надежностью, малыми габаритными размерами и низкой стоимостью. Это способствует расширению областей примене­ния цифровой обработки сигналов, которую используют при автомати­ческом регулировании процессов в промышленности и на транспорте. Устройства, осуществляющие линейную фильтрацию сигналов цифро­выми методами (т. е. с использованием средств цифровой вычислитель­ной техники), получили название цифровых фильтров.

Если определена функция передачи F(z) цифрового фильтра, свой­ства которого повторяют свойства аналогового фильтра-прототипа с функцией передачи F(p), то по ней просто строится каноническая схема, которую можно рассматривать как алгоритм обработки сигнала. Цифровую фильтрацию сигналов осуществляют на основе выполнения операций только трех типов: задержки, сложения и умножения. По­этому алгоритм цифровой обработки может быть реализован двумя способами: универсальной ЭВМ, выполняющей цифровую обработку по специальной программе, или специализированным вычислительным устройством, выполняющим только три указанные выше операции. Первый способ реализации алгоритма цифровой фильтрации называют программным, второй — аппаратурным.

Программный способ реализации эффективен при модели­ровании различных систем цифровой обработки сигналов, так как поз­воляет легко изменять алгоритм фильтрации. Цифровые фильтры, предназначенные для работы в системах автоматики, телемеханики и связи, должны обрабатывать сигналы в реальном масштабе времени, т. е. за время, не большее периода дискретизации входных сигналов, что является их особенностью. Использование универсальных ЭВМ для этих целей практически невозможно из-за их сравнительно низ­кого быстродействия и значительной стоимости. Аппаратур­ная реализация цифровых фильтров основана на использовании циф­ровых интегральных схем, представляющих собой регистры сдвига, сумматоры, умножители и т. п. Она стала возможной в связи с появле­нием в последние годы больших интегральных схем, имеющих большие функциональные возможности и высокое быстродействие.

По сравнению с аналоговыми цифровые фильтры имеют ряд досто­инств, к которым относят высокую стабильность параметров, простоту изменения характеристик, хорошую их повторяемость в процессе про­изводства. При использовании цифровых фильтров не возникает задачи согласования нагрузок, они могут работать в диапазоне от сверхниз­ких частот до частот, измеряемых мегагерцами. Вместе с тем цифровым фильтрам присущи и некоторые специфические особенности, обуслов­ленные цифровым характером обработки сигналов, о Цифровые фильтры используют в системах управления различными объектами и процессами, где алгоритмы обработки могут быть настоль­ко сложными, что аналоговыми устройствами реализованы быть не могут. Другая важная область применения цифровых фильтров — это обработка низко- и инфранизкочастотных сигналов, когда использо­вание аналоговых устройств затруднено из-за больших габаритных размеров катушек индуктивностей и конденсаторов. Области приме­нения цифровых фильтров будут непрерывно расширяться в связи с по­явлением и широким распространением микропроцессоров, специали­зированных БИС ит. п., уменьшением их стоимости и повышением быс­тродействия.

На железнодорожном транспорте цифровые методы обработки сигна­лов, и в частности цифровые фильтры, смогут найти применение в пер­спективных системах связи, например в устройствах сопряжения систем передачи с частотным и временным разделениями каналов (транс­мультиплексорах), во вновь разрабатываемых устройствах железнодо­рожной автоматики.

ЛИНЕЙНАЯ МОДЕЛЬ ЦИФРОВОГО ФИЛЬТРА. НЕРЕКУРСИВНЫЕ И РЕКУРСИВНЫЕ ФИЛЬТРЫ. Понятие фильтр будем использовать в широком смысле как уст­ройство для обработки сигнала заданным способом. Как отмечалось, частотные фильтры, пропускающие определенные полосы частотных составляющих, являются одной из разновидностей фильтров.

Поскольку цифровой фильтр обрабатывает сигналы на основе ис­пользования вычислительной техники, то сигнал, поступающий на вход вычислительного устройства, должен быть цифровым, т. е. дис­кретным и квантованным. Как правило, исходный, подлежащий обра­ботке сигнал является аналоговым, поэтому на первом этапе цифровой обработки его преобразуют в цифровой дискретизацией и квантова­нием, что осуществляет устройство, называемое аналого-цифровымпреобразователем (АЦП).

Дискретизация представляет собой замену непрерывного во времени сигнала последовательностью отсчетов (выборок), взятых че­рез определенные интервалы времени. Ранее отмечалось, что дискре­тизация должна осуществляться с частотой, достаточной для сохра­нения точности представления непрерывного сигнала. Квантование — это замена выборок напряжения дискретного сигнала, каж­дая из которых может принимать бесчисленное множество значений, выборками напряжения, принимающими одно из конечного числа значений.

Квантование эквивалентно округлению числа при вычислениях и должно осущест­вляться с необходимой для решения задачи точностью. В результате выполнения опера­ций дискретизации и квантования сигнал на выходе АЦП есть последовательность выборок сигнала, представленных в виде, пригодном для обработки вычислительным устройством.

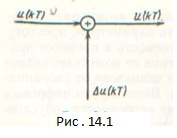
Квантование отсчета (выборки) можно рассматривать как появление в тракте обработки сигнала некоторой помехи, максимальное значение которой не превышает половины шага квантования. Последнее можно представить схемой (рис. 14.1), гдеu_кв(kT)— квантованное значение выборки; ∆u(kT) — погрешность представления выборки сигнала и (kT), обусловленная квантованием. Если погрешность квантования пренебрежимо мала, то можно считать, что фильтр осуществляет пре­образования точных значений выборок дискретизированного сигнала. Такой фильтр называют дискретным. Если требуется учет по­грешности, вызванной квантованием выборок дискретизированного аналогового сигнала, то возникновение и преобразование этой по­грешности цифровым фильтром следует рассматривать совместно с пре­образованием квантованных отсчетов, пользуясь при этом представ­лением выборок сигнала, показанным на рис. 14.1.

Таким образом, в обоих случаях можно рассматривать прохожде­ние через фильтр последовательности отсчетов дискретного сигнала. При этом, как отмечалось в главе 1, для цепей, находящихся под воз­действием дискретных сигналов, можно использовать те же характери­стики, что и для аналоговых цепей. Реакцию цепи на единичный им­пульс называют импульснойхарактеристикой цепи. Для аналоговых цепей она представляет собой непрерыв­ную функцию G (t). Если единичный импульс

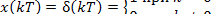
подать на вход цифрового фильтра, то сигнал на его выходе будет пред­ставлять собой дискретную последовательность значений, следующих с интерваломТ, называемым интерваломдискретизации. Этот сигнал является импульснойхарактеристи­койцифровогофильтра.

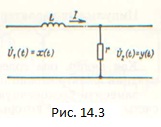
При воздействии на цепь с импульсной характеристикой G (kT) сигналом, представляющим собой последовательность значений х (kT), выходной сигнал по аналогии с интегралом свертки (1.14) определя­ется дискретной сверткой:

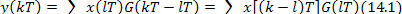
Формула (14.1) определяет значение k-йвыходной выборки. Для на­хождения выходного сигнала ее следует применить многократно для последовательного вычисления у(0); у (Т)\ у (2Т) и т.д.

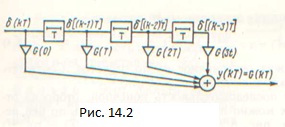
Реакция фильтра на единичный импульс:

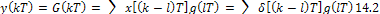
Если реакция фильтра на единичный импульс представлена конеч­ным числом отсчетов, то G (kT) состоит из конечного числа членовK. В этом случае и реакция фильтра у (kT) на сигнал, представляемый конечным числом отсчетов х (kT), имеет конечное число отсчетов. Так, например, приК= 3 импульсная характеристика фильтра определя­ется четырьмя значениями:

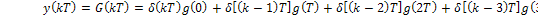
Последнему выражению соответствует схема (рис. 14.2), которая входную последовательность отсчетов х (kT) преобразует в выходную у (kT) и представляет собой дискретный фильтр с импульсной характе­ристикой G (kT).Эта схема является также моделью цифрового фильт­ра, в которой не учитываются погрешности квантования.Такую модель называют линейной.На схему, приведенную на рис. 14.2, можно смотреть и как на форму представления алгоритма преобразования х (kT) ву (kT) в соответствии с выражением (14.1). Рассмотренный фильтр не имеет цепей обратной связи и называется нерекур­сивным.

Для практической реализации нерекурсивного фильтра импульс­ная характеристика G (kT) должна представлять собой последователь­ность с конечным числом членов.

Если импульсная характеристика содержит бесконечное число от­счетов, быстро убывающих по значению, то можно, отбросив отсчеты с малыми значениями, ограничиться конечным их числом. Если же отсчеты импульсной характеристики не убывают по значению, то не­рекурсивный фильтр реализовать невозможно.

Пусть, например, необходимо создать цифровой фильтр, эквива­лентный цепи (рис. 14.3), которую в этом случае называют фильтром-прототипом. Такая цепь была рассмотрена в § 1.1, а ее импульсная характеристика (см. § 1.5) имеет вид:

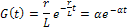
Импульсная характеристика дискретного фильтра:

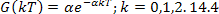
Как видно, она содержит бесконечное число отсчетов. Соответст­вующий фильтр можно построить двумя способами:

заменить бесконечную последовательность конечной, отбросив от­счеты, значением которых можно пренебречь, и построить по ней не­рекурсивный фильтр (см. рис. 14.2), где G(0) = α; G(T) =αe^-αt;G(2T) =αe^-2αt; G(3T) =αe^-3αtи т. д.;

охарактеризовать цепь дифференциальным уравнением, которое (см. § 1.2) имеет вид:

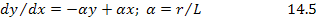
и перейти от него к разностному.

В § 1.1, переходя к разностному уравнению, мы заменяли на 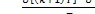, а в теории цифровой фильтрации заменяютна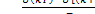

При этом дифференциальное уравнение (14.5) переходит в разностное:

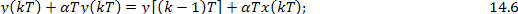
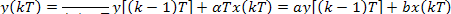
Имея в виду, что αТ-малая величина, 1+αТ- можно рассматривать как приближенное представление 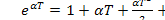и положить .

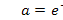Коэффициент x(kT) при b=αТобеспечивает физическую экви­валентность при замене непрерывного воздействия х (t) последова­тельностью импульсов с амплитудами х (kT). Таким должен быть ко­эффициент bпри дискретной фильтрации. При цифровой обработке сигналов физическое значение импульсов несущественно, множитель T в выражении коэффициента bявляется масштабным и может быть при­нят равным единице и тогда b = α.

Уравнение (в.6) можно переписать в виде

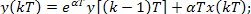
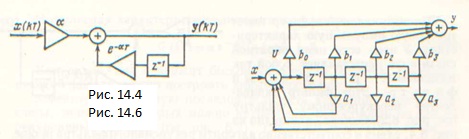
Выражению (14.7) соответствует схема (рис. 14.4). При подаче на ее вход сигнала

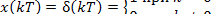
на выходе последовательно будут получаться:

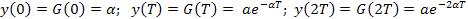
Рассматриваемый фильтр имеет требуемую импульсную характери­стику. У него есть цепь обратной связи и он представляет собой так называемый рекурсивный фильтр. Этот фильтр эквива­лентен нерекурсивному фильтру

(см. рис. 14.2). Однако, как видно из рис. 14.4, схема и соответственно алгоритм рекурсивного фильтра проще, чем нерекурсивного. Так, для определения одного значения выходного сигнала для нерекурсивного фильтра требуется выполнить 2/С операций, а для рекурсивного — только две операции. Поэтому если импульсная характеристика цифрового (дискретного) фильтра должна иметь боль­шое число отсчетов, то целесообразно использовать рекурсивные схемы. Нерекурсивную схему следует применять при реализации фильтров с импульсной характеристикой, содержащей небольшое число отсчетов. В технической литературе, посвященной цифровым и дискретным фильтрам, использована и другая терминология: фильтры с конечной импульсной характеристикой (КИХ-фильтры) и с бесконечной им­пульсной характеристикой (БИХ-фильтры). Любой реальный нере­курсивный фильтр является и КИХ-фильтром. Рекурсивные фильтры, как правило, есть БИХ-фильтры, однако возможно построение рекурсивных фильтров, представляющих собой КИХ-фильтры.

ОПЕРАТОРНЫЕ ХАРАКТЕРИСТИКИ И КАНОНИЧЕСКИЕ СХЕМЫ ЦИФРОВЫХ ФИЛЬТРОВ. В главе 1 при рассмотрении способов представления сигналов и характеристик цепей было показано, что в дискретном случае преобра­зованию Лапласа, переводящему функции времени х (t) в X (p), соот­ветствует z-преобразование, переводящее x(kT) в Х(z), где z = e^pT. Физически оператору z^-1=e^-pTсоответствует задержка сигнала на время Т .

Применим z-преобразование к разностному уравнению (14.7):

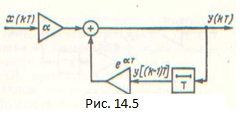
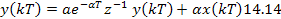Соответствующая выражению (14.14) схема приведена на рис. 14.5. Применяя к этой схеме правило определения передаточной функции цепи с обратной связью, найдем:

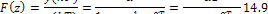
Функция (14.9) и схема, приведенная на рис. 14.5, представляют собой фильтр первого порядка. Функция F(z) является рациональной дробью относительно ги называется системнойилипере­даточнойфункцией фильтра. Более сложные фильтры имеют и более сложные характеристики.

В общем по аналогии с F (р) функцию F (z) можно представить в виде

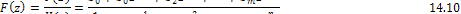
По аналогии с каноническими схемами передающих цепей, рас­смотренными в § 2.24, составим каноническую схему цифрового (дис­кретного) фильтра третьего порядка (рис. 14.6) с характеристикой

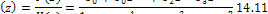
Для пояснения ее действия введем промежуточную переменную U. Из условия равновесия для левого сумматора найдем:

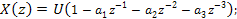
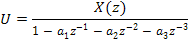
Выход Y (z) в свою очередь равен U( ). Отсюда F(z)=Y (z)/X (z) дает выражение (14.11).

Очевидно, что для построения цифровых фильтров могут быть ис­пользованы и другие канонические схемы, и, в частности, схемы кас­кадного и параллельного соединений нескольких фильтров первого или второго порядка.

14.4. ПРИЕМЫ ПОСТРОЕНИЯ ЦИФРОВЫХ ФИЛЬТРОВ ПО ЗАДАННЫМ ХАРАКТЕРИСТИКАМ

Как отмечалось, задача построения нерекурсивного фильтра по заданной импульсной характеристике решается просто. Однако чаще бывает задана его частотная (или операторная) характеристика. По­скольку методы аппроксимации желательных характеристик частот­ных фильтров рациональными функциями передачи F (р) с максималь­но плоскими и равноволновыми характеристиками хорошо разработаны (см. § 6.14), то будем считать, что требуемая характеристика задана функцией F (р) вида

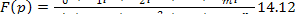
Она является характеристикой аналогового фильтра-прототипа. Задача заключается в переходе от функции F (р) к функции F (z). По F(z), как было показано, строится одна из канонических схем, чем и определяется алгоритм работы цифрового фильтра.

Сложность перехода от F (р) к F(z), несмотря на сходство формул (14.10) и (14.12), заключается в однозначном соответствии функции F (р) дифференциальному уравнению, а функции F (z) разностному урав­нению. При переходе от дифференциального уравнения к разностному меняются значения коэффициентов, как это было видно из рассмотрен­ного в § 2.14 простого примера.

Коэффициент а в дифференциальном уравнении преобразовался 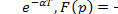в -в 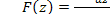В ряде простых случаеможно пользоваться таблицей соответствий между L-и z-преобразованиями (см. табл. 1.2).

Иногда функцию F (р) можно разложить на простые дроби вида а/(р + а) и воспользоваться известными соответствиями, но в боль­шинстве практически важных случаев приходится искать другие прие­мы преобразования F (р) в F(г).

На практике применяют так называемое билинейное z-преобразование, при котором используют подстановку

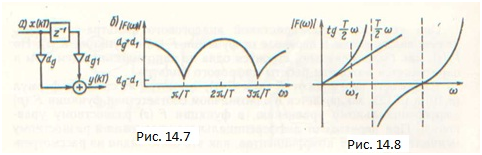
Это преобразование было найдено формально математически при поисках способа преобразования комплексной плоскости рв плоскость z. Пояснить его можно так. Заметим, что частотные характеристики дискретных фильтров, как и спектры дискретных сигналов, периодич­ны. Проиллюстрируем это на примере простого нерекурсивного фильт­ра (рис. 14.7, а). Для него

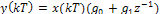
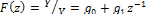
Имея в виду, что 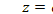и 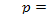, получим:

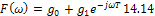
Выражение (14.14) содержит два слагаемых: вектор направленныйвдоль вещественной оси, и вращающийся вектор 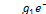.Модуль функции F( ) будет периодически изменяться от 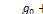до 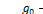(рис 14.7,б).

Таким образом, задачу перехода от функции F (р) к функции F (г) можно сформулировать как задачу перехода от непериодической частотной характеристики к периодической. Характеристика должна повторяться далеко вне рабочего диапазона частот, ^то легко дости­гается выбором периода дискретизации соответственно малым (см. рис. 14.7, б). И поскольку повторение характеристики происходит вне рабочего диапазона, как она повторяется—безразлично.

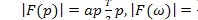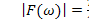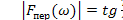Рассмотрим теперь функции Пусть рабочий диапазон кончается в точке .Введем теперь периодичность, заменив на (рис. 14.14). В рабочем диа­пазоне частот, т. е. при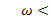

Равенству (14.15) соответствует соотношение

и, следовательно,

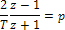
Из рис. 14.8 видно, что вблизи со_х происходит расхождение между x и tgx. Его можно уменьшить введением преобразования масштаба частот:

где 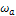— частота среза аналогового фильтра-прототипа;

— частота цифрового фильтра, на которой характеристики фильтров должны совпадать.

Как видно, при tgx = х выражение (14.17) дает = . В соот­ветствии с выражением (14.17) следует пересчитывать частоты среза и частоты, на которых должно гарантироваться определенное ослабление. С учетом сказанного, а также, имея в виду, что F (г) должны быть пред­ставлены в виде функции от , дробно-рациональное преобразование (14.15) для ФНЧ имеет вид:

Пусть, например, требуется рассчитать цифровой фильтр нижних частот с максимально плоской характеристикой в по­лосе пропускания и затуханием 3 дБ на частоте среза f_с = 1 кГц, ослаблением не менее 20 дБ на частоте f₂ = 2 кГц и частотой дискретизации f_д= 10 кГц. Сна­чала определим характерные ча­стоты фильтра-прототипа. Часто­те среза цифрового фильтра 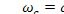соответствует частота среза фильтра-прототипа:

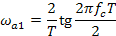
где 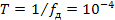— интервал дискретизации.

Подставляя числовые данные, получим 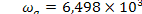. Аналогично частоте цифрового фильтрасоответствует частота фильтра-прототипа:

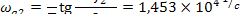
Таким образом, фильтр-прототип должен иметь затухание 3 дБ на частоте = 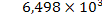затухание не менее 20 дБ на частоте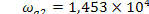

Определим теперь частотную характеристику фильтра-прототипа. Вспомним, что максимально плоскую характеристику имеют фильтры Баттерворта, описываемые выражением

Найдем порядок фильтра-прототипа, удовлетворяющего указан­ным требованиям. Отношение частот c / = 2,236. Задаваясь на частоте ослаблением не менее 20 дБ (т. е. в 10 раз), из выражения (14.19) определим порядок фильтра: (1 + 2,236ⁿ) 100, откуда n 2,85. Принимаем n= 3. Фильтр Баттерворта третьего порядка на частоте обеспечивает ослабление сигнала, равное 10 lg [1 ++ (2,236)⁶] ≈21 дБ, что превышает заданные требования к фильтру. Найдем теперь передаточную функцию фильтра-прототипа — фильтра Баттерворта третьего порядка. Согласно табл. 6.3 можно написать:

Откуда

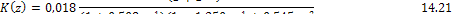
Системная функция (14.21) может быть реализована в виде цепочеч­ного соединения двух фильтров первого и второго порядка, для чего эту функцию представим в виде произведения двух системных функций:

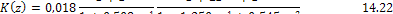
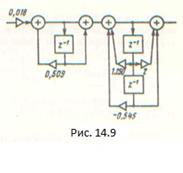
Схема цифрового фильтра, соответствующая системной функции (14.22), приведена на рис. 14.9.