ИЗУЧЕНИЕ РАСПРЕДЕЛЕНИЯ ВРЕМЕНИ ПРЕБЫВАНИЯ
Особенности структуры потока, связанные с продольным перемешиванием, одновременно связаны с неравномерностью времени пребывания. Поэтому один из лучших способов определить, какова структура данного потока,— это исследовать в нем распределение времени пребывания.
Задача заключается в следующем. Через аппарат движется поток. В какой-то момент мы отбираем на выходе пробу жидкости. И теперь хотим узнать, какая доля жидкости в этой пробе вошла в аппарат секунду назад, какая — две, три, четыре и т. д. Но как это сделать? Ведь разные частицы пробы для нас неразличимы. Давайте сделаем их различными. Для этого выделим среди всех частиц потока те, которые вошли в аппарат в какой-то определенный момент. С этой целью мы их пометим. Обычно это делается так. В определенный момент (в дальнейшем будем принимать его за начало отсчета времени, τ=0) в жидкость на входе коротким импульсом добавляется малое количество добавки-индикатора (ее называют также «трассер»). Теперь, если на выходе появится меченая частица, нам будет точно известно, когда она вошла в аппарат и, следовательно, сколько времени она в нем пробыла. Нам достаточно получить лишь зависимость концентрации индикатора на выходе из аппарата от времени (си от τ), поскольку она в определенном смысле представляет собой портрет распределения времени пребывания.
Что можно использовать в качестве индикатора? Эта примесь должна обладать следующими свойствами. Во-первых, она не должна влиять на движение потока. Отсюда прежде всего следует, что индикатора нужно добавлять очень мало. Во-вторых, с индикатором внутри аппарата ничего не должно происходить: он не должен вступать в реакцию, оседать на стенках и внутренних деталях аппарата. Единственное его назначение — двигаться вместе с мечеными частицами. Наконец, в-третьих, он должен быть легко идентифицирован на выходе.
Если движущаяся в аппарате фаза — вода, то индикатором может быть раствор красителя (на выходе мы поставим колориметр) или раствор электролита (на выходе — измеритель электропроводности, кондуктометр). Если движется воздух, то в качестве примеси чаще всего используют газ, сильно отличающийся по теплопроводности: гелий (теплопроводность велика) или СО2 (теплопроводность мала). На выходе — датчик теплопроводности.
Теперь подробнее исследуем зависимость Си от τ. Рассмотрение этого вопроса существенно упрощается, если привести Си и τ к безразмерному (приведенному) виду. Операция приведения очень широко распространена в физике, и сейчас мы немного отвлечемся, чтобы поговорить об этом.
Что значит измерить какую-то величину? Это — сравнить ее с неким эталоном. Измерить длину — сравнить длину данного предмета с длиной платиновой линейки, хранящейся в Севре (или, более современно, с длиной волны излучения, полученного в строго определенных условиях). Измерить массу — опять же сопоставить массу предмета с массой эталона килограмма и т. д. Каждый раз эталон — нечто совершенно чуждое данному конкретному измерению и зато общее всем измерениям данной величины.
Но можно поступать и иначе. Предположим, мы захотим определить размеры конкретной человеческой фигуры. И в качестве единицы (эталона) примем не метр, не сантиметр и даже не фут, а рост этого человека. Тогда , например, получится: ширина плеч — 0,276; окружность груди — 0,596; длина руки — 0,447 и т. д.
Если теперь попытаться по этим данным восстановить фигуру, то окажется, что полученный набор чисел одинаково хорошо подходит и к самому человеку, и к статуэтке высотой 20 см, и к статуе в два человеческих роста. Эти числа определяют не размер предмета, а только его пропорции. При таком способе измерения все подобные предметы неразличимы.
Хорошо это или плохо? С одной стороны, описание внешности оказалось явно неполным. Вы так и не поняли, какого он роста (скрывать не станем — 180 см). Лишь после указания роста этот набор чисел оказался связанным с эталоном, а значит, и с остальными предметами окружающего мира. Но зато получена характеристика, обладающая общностью: ею описывается не только конкретный человек, но и ряд возможных его изображений в разных масштабах.
Эти соображения оказались особенно важными после того, как понятие подобия удалось распространить на все физические величины и явления. Можно говорить о подобии движения в потоках, подобии протекания химических реакций и т. д. Около века назад оформилась теория подобия, анализирующая явления с позиций их подобия. Одна из важнейших возможностей, даваемых этой теорией, как раз и заключается в обобщенном характере описаний — описав поведение одного объекта, мы получаем характеристику любого объекта, подобного данному; достаточно только учесть его размер (масштаб). Если наш первый объект — модель какого-то практически важного оригинала, то теория подобия определяет правило переноса полученных зависимостей с модели на оригинал и, таким образом, является одной из основ моделирования.
Одна из особенностей теории подобия — использование безразмерных величин, т. е. величин, не связанных с общими эталонами, о которых говорилось вначале (размерность, по сути дела,— это и есть соотнесение с эталоном). Простейший способ получения безразмерной величины уже рассмотрен нами: сопоставление результатов измерения с принятым за единицу внутренним эталоном (в рассмотренном примере это был рост), характеризующим данную конкретную задачу. (Есть и более сложные способы: так, использованное нами при описании турбулентного потока число Рейнольдса, по сути, представляет собой безразмерную скорость.)
Теперь вернемся к распределению времени пребывания. Чтобы выразить τи Си в безразмерном виде, выберем внутренние эталоны (единицы). В качестве единицы времени естественно принять среднее время пребывания 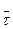 =VP/VC Безразмерное время т для любого момента / будет равно
=VP/VC Безразмерное время т для любого момента / будет равно
τ=τ/ 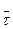 . (22)
. (22)
Единица концентрации Со определяется следующим образом. Обозначим количество индикатора, введенное на входе, g0, тогда
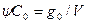 (23)
(23)
Для безразмерной концентрации С индикатора на выходе имеем C=Cи/С0
Переход от переменных τ, СИ к безразмерным τ и С сразу же позволяет распространять полученные результаты на группу подобных друг другу случаев. Особенно ясно это преимущество в отношении величины с„. Ведь си пропорционально gо, т. е. чем больше мы введем индикатора, тем большую концентрацию получим; но gо — величина, не имеющая отношения к характеру потока, связанная со случайными обстоятельствами опыта. В то же время С не зависит от этих обстоятельств. Использование τ также удобно: установив условия подобия (в ряде случаев это удается сделать), мы получаем одинаковое описание и небольшой лабораторной модели с малым средним временем пребывания, и большого промышленного аппарата, где время велико. Есть и другое преимущество безразмерных переменных, но о нем мы поговорим немного позже.
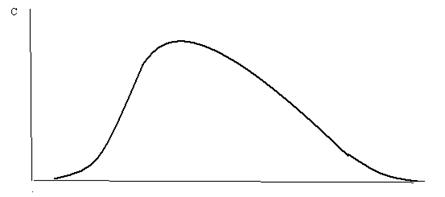
Рис. 10. Зависимость безразмерной концентрации от безразмерного времени
Итак, наш опыт с вводом индикатора дал зависимость С от τ. Типичный (хотя далеко не единственно возможный) график функции С(τ) показан на рис. 10. Вначале на выходе нет индикатора. Затем появляются первые его порции — те, которые метят частицы с наименьшим временем пребывания. Потом С становится больше, проходит через максимум и начинает убывать: основная масса индикатора прошла, и выходит то, что задержалось в зонах циркуляции и застоя. Через достаточно большое время концентрация С практически падает до нуля, хотя теоретически не исключается и асимптотический характер приближения кривой зависимости к нулю.
Дальнейшее выяснение физического смысла функции С(τ) связано с одним из фундаментальных понятий современной математики — случайной величиной, о которой заранее нельзя точно сказать, какое значение примет она при нашем измерении. Мы не знаем, сколько зернышек окажется в арбузе, который собираемся разрезать; не знаем, каким будет время пребывания какой-то одной частицы из числа тех, которые в данный момент входят в аппарат. И число зернышек, и время — случайные величины.
Но чтобы наша величина в качестве случайной стала предметом научного рассмотрения, необходимо, чтобы эксперимент по ее измерению можно было проводить многократно, и каждый раз эта величина должна оставаться случайной. Например, мы заранее не знаем, сколько гор окажется на Титане — спутнике Сатурна. Но это не случайная величина: один раз сосчитаем и будем знать навсегда.
Важнейшая характеристика случайной величины — вероятность. Строго определить, что это такое, очень сложно. Нас удовлетворит приблизительное описание, не претендующее на строгость. Вероятность показывает, как часто в измерениях будет получаться данное значение величины. Но ведь величина — случайная, и в разных сериях измерений частота ее появления окажется различной (иначе мы заранее бы знали, когда что получится). Это верно; но если числе измерений будет становиться все больше и больше, то эта частота окажется во ближе и ближе к вероятности. Вероятность и есть в некотором (не вполне строгом) смысле тот предел, к которому стремится частота при увеличении числа измерений и вокруг которого она колеблется в различных сериях.
Вероятность Р любого значения случайной величины заключена в предела от 0 до 1. Если Р=0, то данное значение практически никогда не появится в измерениях. Если Р=1, то во всех измерениях наверняка будет получаться именно данное значение. Например, если мы станем подсчитывать количество певчих птиц в ближайшей роще, вероятность того, что их число составит 109 равна 0 (наверняка в роще не поместится миллиард птиц). Вероятность, равна 1, характеризует величины неслучайные. Так, сейчас у Земли с вероятностью имеется один крупный естественный спутник. В некоторых простых ситуациях определить вероятность можно исходя и числа возможных равновероятных результатов измерений. Скажем, при бросании игральной кости (кубика) вероятность того, что выпадет 5, равна 1/6. Для шести возможных вариантов вероятность того, что выпадет хотя бы один из них, равна 1, а вероятность любого конкретного варианта в 6 раз меньше. Все примеры, рассмотренные в предыдущем абзаце, относятся к одному классу случайных величин, так называемым дискретным. У этих величин их возможные значения — не любые, а отделены друг от друга каким-то интервалом. Число птиц, спутников, число очков при бросании кости — обязательно целые числа. Не может быть у планеты, скажем, 2,3 спутника. Есть дискретные величины, где интервал и не целый. Например, суммарный спин систем электронов может принимать значения, отделенные друг от друга интервалами, кратными ½. Но в любом случае у дискретных величин эти интервалы есть.
Другой случай — непрерывные случайные величины, к ним относятся масса, время, скорость и т. п. Здесь в некоторой области может получиться любое значение. Время может составить 1 с, 2 с, но может и 1,08356 с, и какое угодно другое значение.
Для непрерывных случайных величин вероятности приходится задавать по-особому. Дело вот в чем. Вероятность того, что непрерывная случайная величина примет какое-то точно заданное значение, всегда равна 0. Как же так? Ведь какое-то значение обязательно получится. Да, но это будет не то значение, которое мы заранее задали. Мы задали 1,5, а получилось 1,5000001. И даже если получили 1,5000000, никогда нельзя ручаться, что еще через 200 знаков не появится какой-то, отличный от нуля. Бесконечный диапазон возможных значений, как угодно близких к заданному, и приводит к тому, что для заданного значения получаем Р=0.
Но нельзя же сказать, что все значения непрерывной случайной величины равновероятны. Вероятность того, что масса яблока, сорванного с дерева, окажется равной точно 200 г, равна 0. Вероятность того, что эта масса окажется равной точно 200 кг, тоже равна 0. Но ясно, что это в каком-то смысле разные нули: яблоко в 200 г нас не удивит, яблоко в 200 кг совершенно невероятно.
Для того чтобы определить вероятность значения непрерывной случайной величины, это значение надо задать не точно, а с каким-то интервалом. Вероятность того, что масса яблока окажется в пределах от 200 до 200,1 г уже не равна нулю, хотя и мала (потому что мал интервал в 0,1 г).
Записывается этот способ определения вероятности так:
P(x≤ X ≤x+dx)=f(x)dx 25
Смысл формулы (25) таков. Здесь X —. случайная величина; х — какое-то ее значение; dx— бесконечно малое приращение (дифференциал) значения х. Левая часть обозначает вероятность того, что величина х окажется в интервале от х до х+ dx. Теперь обратимся к правой части. Множитель их введен сюда потому, что чем больше интервал, тем скорее «попадет» в него величина. Функция f(x)отражает то обстоятельство, что разные значения х не равновероятны (точнее, что вероятность попасть в интервал шириной dx зависит от того, где на оси х расположен этот интервал). Эта функция называется плотностью вероятности случайной величины.
Так вот, функция С(τ), оказывается, представляет собой плотность вероятности времени пребывания. Если выразить время не в приведенных, а в размерных единицах, то
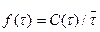 (26)
(26)
где С(τ) — та же самая безразмерная концентрация индикатора (делать ее размерной нет смысла).
Как же можно использовать полученную плотность вероятности, т. е. функцию С(τ) или f(τ)? Прежде всего для ряда случаев знание этой функции позволяет непосредственно рассчитать ход химической реакции. Так, протекание реакции первого порядка (см. формулы 13, 16, 18) в потоке, где распределение времени пребывания характеризуется плотностью вероятности f(τ), дает на выходе такое значение концентрации реагента:
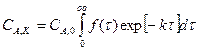 (27)
(27)
Рассчитать этот интеграл не так уж сложно, для чего, например, можно построить график функции  от τ=0 до того значения τ, при котором эта функция для нас неотличима от нуля. Площадь под графиком приближенно равна искомому интегралу. В практических целях обычно пользуются более быстрыми и точными методами численного интегрирования. Формула (27) показывает, что в этом простом случае для расчета процесса достаточно знать уравнение скорости реакции (13) и функцию f(τ), которую можно получить из опыта с пропусканием индикатора.
от τ=0 до того значения τ, при котором эта функция для нас неотличима от нуля. Площадь под графиком приближенно равна искомому интегралу. В практических целях обычно пользуются более быстрыми и точными методами численного интегрирования. Формула (27) показывает, что в этом простом случае для расчета процесса достаточно знать уравнение скорости реакции (13) и функцию f(τ), которую можно получить из опыта с пропусканием индикатора.
В более сложных случаях не всегда можно получить аналогичную формулу. Тогда использование непосредственно функции C(τ)или f(τ)может быть затруднительно. Проще поступать по-другому: рассчитать на основе этой функции некоторые характеристики времени пребывания как случайной величины и дальше пользоваться для анализа этими характеристиками.
Чаще всего рассчитывают две основные характеристики. Первая характеризует среднее значение случайной величины. Раз величина случайная, то и получаемые для нее значения оказываются разными. Но какова она в среднем? Около какого среднего колеблются отдельные ее значения? Оказывается, в теории вероятностей можно определить несколько разных средних. Но чаще всего пользуются характеристикой, которая еще с XVII в. носит название математическое ожидание. Название сегодня мало о чем говорит. Когда-то оно означало ожидаемый средний выигрыш в азартной игре. Азартные игры, особенно кости, оказались прекрасной моделью, на которой изучали свойства вероятностей первые исследователи в этой области. Сейчас интересы математиков переместились на совсем иные вопросы, а термин остался. По существу, математическое ожидание — то же самое, что среднее арифметическое, только записанное так, чтобы можно было рассчитать его через вероятности. Поэтому в дальнейшем будущем будем называть его просто средним и обозначать чертой над усредняемой величиной.
Среднее значение безразмерного времени пребывания определяется формулой
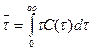 (28)
(28)
Но эта формула практического интереса не представляет. Дело в том, что, приводя время к безразмерному виду, мы приняли среднее время за единицу. И если дальше все правильно, то формула (28.) должна тождественно приводить к результату 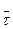 =1. Гораздо интереснее формула, которую можно вывести из (28), позволяющая рассчитать Г из результатов опыта с вводом индикатора
=1. Гораздо интереснее формула, которую можно вывести из (28), позволяющая рассчитать Г из результатов опыта с вводом индикатора
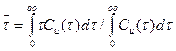 (29)
(29)
Можно возразить — величину 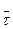 гораздо быстрее и проще рассчитать по формуле (11). Зачем такие сложности?»
гораздо быстрее и проще рассчитать по формуле (11). Зачем такие сложности?»
Формула (29) сложна, это верно. Но зато ее можно использовать тогда, когда неизвестен объем, занимаемый потоком. А затем при помощи формулы (11) определить этот самый неизвестный объем.
Работать таким методом первыми начали, по-видимому, спелеологи. Во многих местах (например, на Южном берегу Крыма) важную роль играют речки, вытекающие из подземных озер, спрятанных в пещерах. Такое озеро служит природным водохранилищем, и его объем важно знать для прогноза поведения реки. Но далеко не всегда удается обмерить озеро непосредственно. Тогда к пещере отправляется экспедиция. Экспедиция делится на два отряда. Один останавливается наверху, в том месте, где река выбивается из-под земли. Замерив расход воды в реке, он ждет. Другой отряд спускается в пещеру. И в заранее обусловленное время (например, ровно в полночь) спелеологи выливают в устье той подземной речки, которая впадает в озеро, бутылку индикатора. Чаще всего используют флюоресцеин. Даже очень разбавленные его растворы ярко флюоресцируют — светятся красивым зеленым светом. Начиная с момента ввода индикатора, наземный отряд каждые полчаса (или час, или 10 минут в зависимости от ожидаемых размеров озера и от расхода воды) отбирает пробы воды для анализа на индикатор. Нужно сказать, зрелище это очень красивое и немного жуткое:
вся вода в реке светится изумрудным сиянием. Говорят, жители глухих уголков Пиренеев, где такие опыты проводил знаменитый французский спелеолог Н. Кастере, никак не могли решить, кто же эти странные люди, заставляющие светиться реки: посланцы сил добрых или дьявольских.
В химической технологии и, близких к ней отраслях объем аппарата всегда известен. Поэтому здесь такая задача встает лишь тогда, когда поток занимает не весь объем. Так, часто через аппарат движутся два потока: сверху — жидкость, а снизу — газ или пар. При этом скорость газа велика, и его время пребывания мало. А вот жидкость находится в аппарате значительно дольше, и если обрабатываемые вещества способны разлагаться, то желательно сделать время пребывания минимальным. Поэтому стоит подобрать такой режим работы, когда объем, занимаемый стекающей жидкостью, невелик и в соответствии с уравнением (11) мало время пребывания. При отладке такого режима эксперимент с вводом индикатора может сослужить неоценимую службу.
Другой пример, когда, наоборот, малое значение I является грозным признаком — это случай образования козла в шахтных печах.. Название звучит несколько комично, но в самом явлении веселого мало. Козел в печи — это прилипший к стенке или к деталям конструкции материал, на который налипают еще и еще порции; постепенно образуется большой ком, давящий на стенку, перегораживающий путь материалу. Если вовремя не принять меры, козел может стать таким большим, что приведет, к аварии с весьма тяжелыми последствиями. В домне, например, козел может весить много тонн. Такая махина способна обрушить футеровку печи, что потребует остановки на капитальный ремонт и причинит громадные убытки.
Самый простой способ обнаружить зарождающийся козел, основан на том, что он, перегораживая путь части движущейся в печи шихты, образует застойную зону, а это ведет к уменьшению рабочего объема и соответственно 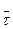 .
.
Теперь еще об одной характеристике случайной величины, очень важной для анализа структуры потока. Это характеристика разброса относительно среднего. Если трехкилограммовый пакет с картофелем содержит 30 клубней, то средняя масса клубня составит 100 г. Но для нас не все равно, будут ли все 30 клубней приблизительно по 100 г (скажем, колебаться от 80 до 120 г) или в пакете будут лежать два гигантских клубня по 1,2 кг, а остальные 28 клубней — мелочь примерно по 20 г. В первом случае все значения массы близки к среднему, во втором наблюдается сильный разброс вокруг него. Наиболее принятая в теории вероятностей мера разброса — дисперсия, представляющая собой среднее значение квадрата отклонения случайной величины от ее математического ожидания (оказалось удобнее изучать квадраты отклонений, чем сами отклонения). Если нам нужно оценить не квадрат, а само отклонение, то достаточно извлечь из дисперсии корень квадратный и получим среднее квадратичное отклонение.
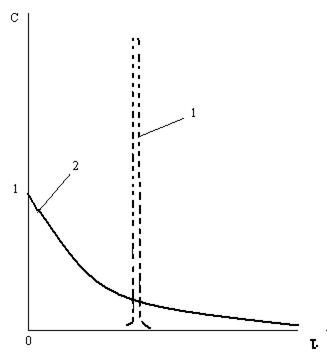
Рис. 9.Плотность вероятности времени пребывания для идеальных потоков: 1 - вытеснение; 2 - смешение
Формула для расчета дисперсии безразмерного времени пребывания 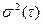 имеет вид
имеет вид
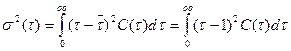 (30)
(30)
В подавляющем большинстве случаев, чем больше дисперсия, тем дальше поток от идеального вытеснения. Для того чтобы яснее представить себе это, рассмотрим плотности вероятности для тех типов потока, которые были рассмотрены раньше.
 Для идеальных потоков графики С(т) показаны на рис. 9. Для идеального вытеснения, строго говоря, график построить нельзя. Действительно, опишем поведение индикатора, движущегося с потоком в аппарате идеального вытеснения. При этом нам придется учесть одно свойство плотности вероятности (физически достаточно очевидное), согласно которому всегда
Для идеальных потоков графики С(т) показаны на рис. 9. Для идеального вытеснения, строго говоря, график построить нельзя. Действительно, опишем поведение индикатора, движущегося с потоком в аппарате идеального вытеснения. При этом нам придется учесть одно свойство плотности вероятности (физически достаточно очевидное), согласно которому всегда
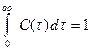 (31)
(31)
Левая часть выражения (31) задает вероятность того, что время пребывания частицы в интервале от 0 до ∞ примет какое-то значение, что будет в любом случае, поэтому соответствующая вероятность и равна единице.
Теперь рассмотрим движение индикатора. Для любого τ <1 на выходе нет индикатора: си=0, С=0. Все частицы, помеченные индикатором, движутся вместе, и ни одна из них еще не появилась на выходе. То же верно и для любого т>1; все меченые частицы уже вышли. При τ= 1 все частицы выходят одновременно. На графике должен быть скачок вверх-вниз (пик), причем ширина этого пика равна нулю. Но мы уже говорили, что интеграл равен площади под кривой. Уравнение (31) требует, чтобы эта площадь была равна 1; тогда высоту пика придется считать бесконечной. Очень странная получается функция: всюду, кроме одной точки, она равна нулю; а в этой точке — бесконечный пик с площадью, равной 1. До начала нашего века такое, пожалуй, и функцией бы не назвали. Потом эта функция остро понадобилась физикам, и один из величайших физиков XX в. П. Дирак ее ввел и назвал дельта-функцией. То, что показано на рис. 11, лишь весьма отдаленное подобие дельта-функции, которую точно изобразить невозможно.
Для идеального смешения функции С(т) совсем другая. Она описывается формулой
С=ехр[-τ] (32)
Тоже довольно необычная зависимость. В этом потоке наиболее вероятно, что время пребывания частицы окажется очень близким к нулю: не успеет она войти в аппарат, как идеальная мешалка перекинет ее к выходу, и частица покидает аппарат, не успев принять участие в реакции (об этом мы уже говорили). Наряду с такими частицами есть и другие, хотя и в гораздо меньшем количестве. Они долго странствуют по аппарату, перемешиваемые по всему объему, и теоретически на выходе могут найтись частицы, вошедшие в аппарат как угодно давно.
Дисперсия времени пребывания для потока идеального вытеснения равна нулю, здесь никакого разброса вокруг среднего нет. Для потока идеального смешения а2(т) = 1. Расчет легко провести по формулам (30) и (32).
Для очень многих реальных потоков величина σ2(τ) лежит между 0 и 1. Их в первом приближении можно рассматривать как промежуточные случаи между обоими идеальными потоками. Но возможны иные случаи, и об этом мы уже говорили. Разумеется, исключен вариант, когда σ2(τ) <0, но больше единицы дисперсия может быть, и теоретически может встретиться сколь угодно большое значение σ2(τ). Правда, если σ2(τ) >1, то это означает, как правило, чрезвычайно плохую организацию потока; обычно так получается, когда в аппарате имеется очень большая застойная зона, а движущийся поток проходит малой частью объема и поэтому весьма быстро. Другой вариант, приводящий к большим значениям σ2(τ) , напоминает предыдущий: это случай резкой неравномерности потока по поперечному сечению, когда нет настоящей застойной зоны, но в одних частях сечения скорость в несколько раз больше, чем в других. К сожалению, этот вариант довольно часто встречается в аппаратах большого поперечного сечения, и создание агрегатов большой единичной мощности ставит перед исследователями непростую задачу: добиваться равномерности потока в крупномерных аппаратах. Наконец, проследим поведение функции С(τ) для каскада аппаратов смешения 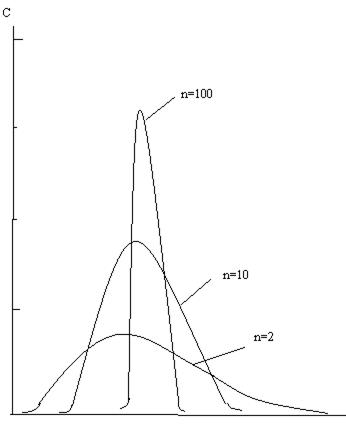
Рис. 10. Плотность вероятности времени пребывания для каскада аппаратов смешения
. Графики на рис. 10 построены с учетом того, что 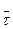 — среднее время пребывания во всем каскаде, рассматриваемом как один аппарат. Уже при п=2 график непохож на идеальное смешение (п=1):С=0 при τ=0, а затем кривая проходит через максимум. Чем больше п, тем круче и выше пик; как мы уже отмечали, предел n → ∞ coответствует переходу к дельта-функции.
— среднее время пребывания во всем каскаде, рассматриваемом как один аппарат. Уже при п=2 график непохож на идеальное смешение (п=1):С=0 при τ=0, а затем кривая проходит через максимум. Чем больше п, тем круче и выше пик; как мы уже отмечали, предел n → ∞ coответствует переходу к дельта-функции.
Интересно выражение для дисперсии:
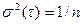 (33)
(33)
Довольно часто понятие каскада используют в качестве схемы, с той или иной степенью приближения описывающей реальный поток, отличающийся от обоих идеальных типов. Тогда один аппарат каскада рассматривают как участок аппарата (ячейку). Такую схему называют ячеечной моделью потока. Эксперимент с вводом индикатора позволяет по формуле (33) легко определить параметр модели — число ячеек, при котором схема лучше всего соответствует нашему потоку.
Дата добавления: 2017-01-08; просмотров: 2244;











