Цифроаналоговые преобразователи

Цифроаналоговые преобразователи (ЦАП) предназначены для преобразования цифровых сигналов в аналоговые. Такое преобразование необходимо, например, при восстановлении аналогового сигнала, предварительно преобразованного в цифровой, для передачи на большое расстояние, в устройствах измерительной техники и ряде других случаев. Другой пример использования такого преобразования – получение управляющего сигнала при цифровом управлении устройствами, режим работы которых определяется непосредственно аналоговым сигналом (например, при управлении двигателями).

К основным параметрам ЦАП относят: разрешающую способность, время установления, погрешность нелинейности. Разрешающая способность – величина, обратная максимальному числу шагов квантования выходного аналогового сигнала. Время установления – интервал времени от подачи на вход до момента, когда выходной сигнал войдет в заданные пределы, определяемые погрешностью. Погрешность нелинейности – максимальное отклонение графика зависимости выходного напряжения от напряжения, задаваемого цифровым сигналом, по отношению к идеальной прямой во всем диапазоне преобразования.

Как и рассматриваемые ниже аналого-цифровые преобразователи (АЦП), ЦАП являются «связующим звеном» между аналоговой и цифровой электроникой. Существуют различные принципы построения ЦАП.

Рассмотрим наиболее используемые из них. На рис. 14.1 приведена схема ЦАП с суммированием весовых токов.

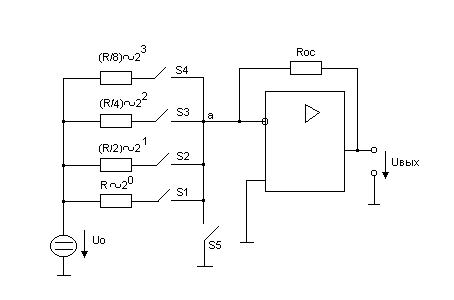
Рис. 14.1

Ключ S5 замкнут только тогда, когда разомкнуты все ключи S1...S4 (при этом 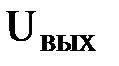= 0). U₀ – опорное напряжение. Каждый резистор во входной цепи соответствует определенному разряду двоичного числа.

По существу этот ЦАП – инвертирующий усилитель на основе операционного усилителя. Проведем анализ работы такой схемы. Так, если замкнут один ключ S1,то 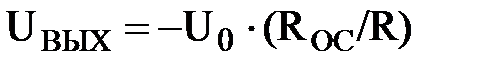, что соответствует единице в первом и нулям в остальных разрядах.

Из анализа схемы следует, что модуль выходного напряжения пропорционален числу, двоичный код которого определяется положением ключей S1...S4. Токи ключей S1...S4 суммируются в точке «а», причем токи различных ключей различны (имеют разный «вес»). Это и определяет название схемы.

Из вышеизложенного следует, что

,

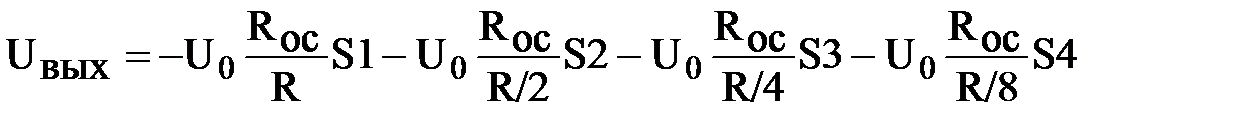т.е. , ( 14.1)

где 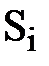(i = 1, 2, 3, 4) принимает значение 1, если соответствующий ключ замкнут, и 0, если ключ разомкнут.

Состояние ключей определяется входным преобразуемым кодом. Схема проста, но имеет недостатки: значительные изменения напряжения на ключах и использование резисторов с сильно отличающимися сопротивлениями. Требуемую точность этих сопротивлений обеспечить затруднительно.

Рассмотрим ЦАП на основе резистивной матрицы R – 2R (матрицы постоянного сопротивления) (рис. 14.2).

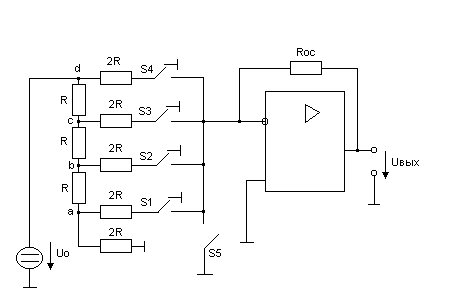
Рис. 14.2

В схеме использованы так называемые перекидные ключи S1...S4, каждый из которых в одном из состояний подключен к общей точке, поэтому напряжения на ключах невелики. Ключ S5 замкнут только тогда, когда все ключи S1...S4 подключены к общей точке. Во входной цепи использованы резисторы всего с двумя различными значениями сопротивлений.

Из анализа схемы можно увидеть, что и для нее модуль выходного напряжения пропорционален числу, двоичный код которого определяется состоянием ключей S1...S4. Анализ легко выполнить, учитывая следующее. Пусть каждый из ключей S1...S4 подключен к общей точке. Тогда, как легко заметить, напряжение относительно общей точки в каждой следующей из точек «а»...«d» в 2 раза больше, чем в предыдущей. 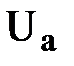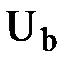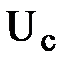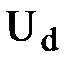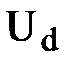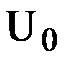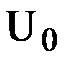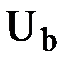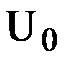К примеру, напряжение в точке «b» в 2 раза больше, чем в точке «а» (напряжения , , и в указанных точках определяются следующим образом: = ; = /2; = /4; 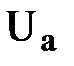= 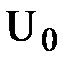/8). Допустим, что состояние указанных ключей изменилось. Тогда напряжения в точках «а»...«d» не изменятся, так как напряжение между входами операционного усилителя практически нулевое.

Из вышеизложенного следует, что:

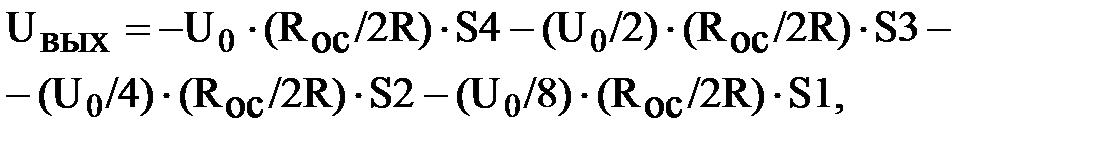
т.е. , (14.2)

где (i = 1, 2, 3, 4) принимает значение 1, если соответствующий ключ замкнут, и 0, если ключ разомкнут.

Приведем схему ЦАП для преобразования двоично-десятичных чисел (рис. 6.3).

Рис. 14.3

Для представления каждого разряда десятичного числа используется отдельная матрица R–2R (обозначены прямоугольниками). Z1...Z4 обозначают числа, определенные состоянием ключей каждой матрицы R – 2R. Принцип действия становится понятным, если учесть, что сопротивление каждой матрицы равно R и выполнить анализ фрагмента схемы, представленного на рис. 14.4.

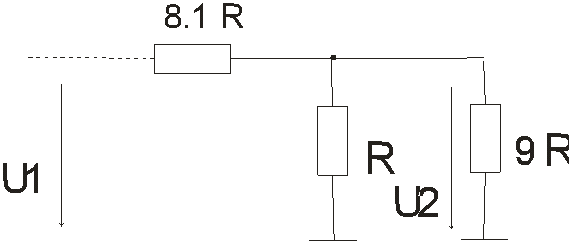
Рис. 14.4

Из анализа следует, что ,

где .

Следовательно, . С учетом этого получим

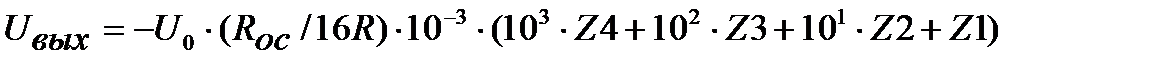. (14.3)

Наиболее распространенными являются ЦАП серий микросхем 572, 594, 1108, 1118 и др. В табл. 14.1 приведены параметры некоторых ЦАП.

Таблица 14.1

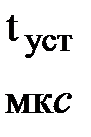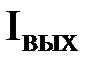Тип схемы	Число разряд.	,	, В	, В/мА	,мА
К594ПА1		3,5	9, +11	(5…15)/2,5 –15/3,5
К1108ПА1		0,4	2,2, +10,5	+5/15 –16/46
К572ПА1А			–17, +17	(5…17)/2
К575ПА2А			–15, +15	5/2 15/2	0,8