Методические указания
Цель работы - использование контурных токов в комплексной форме для расчета несимметричных трехфазных цепей, которые широко применяются в различных электроэнергетических сетях и системах.
Несимметричную трехфазную цепь со статическими нагрузками можно рассматривать как сложную цепь с несколькими источниками ЭДС и рассчитать, используя общие методы расчета электрических цепей в комплексной форме. Расчет целесообразно выполнять по методу контурных токов, так как при этом не требуется преобразование схемы.
По заданной схеме необходимо построить граф и пронумеровать его ветви, которым вместе с источниками присвоить либо первые, либо последние номера. На графе выделить ветви дерева и указать узлы (точки) А, В, С, а также О,О1.
Далее необходимо задать одинаковое направление ветвей с источниками ЭДС 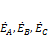 относительно общей точки источников О. Для ветвей с пассивными элементами — комплексными сопротивлениями ZK — целесообразно указать «естественные» направления напряжений (токов) от точек A, В, С к общей точке приемников O1. Некоторые ветви с сопротивлениями ZK могут быть включены на линейные напряжения
относительно общей точки источников О. Для ветвей с пассивными элементами — комплексными сопротивлениями ZK — целесообразно указать «естественные» направления напряжений (токов) от точек A, В, С к общей точке приемников O1. Некоторые ветви с сопротивлениями ZK могут быть включены на линейные напряжения 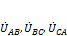 .
.
Для расчета необходимо составить матрицы 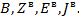 Матрица В составляется по тем же правилам, что и для цепей постоянного тока.
Матрица В составляется по тем же правилам, что и для цепей постоянного тока.
Матрица 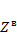 - диагональная и каждый ее ненулевой элемент - это комплексное сопротивление
- диагональная и каждый ее ненулевой элемент - это комплексное сопротивление 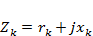 . Значения этих сопротивлений заданы в таблице.
. Значения этих сопротивлений заданы в таблице.
Для расчета на ЭВМ матрица 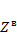 записывается в виде
записывается в виде
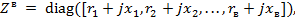 где индекс «в» - номер последней ветви.
где индекс «в» - номер последней ветви.
Если ветвям с источниками 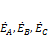 присвоены первые номера 1,2,3, то первые три элемента в матрице
присвоены первые номера 1,2,3, то первые три элемента в матрице 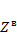 - нулевые.
- нулевые.
Столбцовая матрица 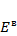 записывается в следующем виде (с учетом того, что ветвям с источниками ЭДС присвоены первые номера):
записывается в следующем виде (с учетом того, что ветвям с источниками ЭДС присвоены первые номера):
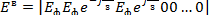 ,
,
где  -заданное фазное напряжение, знак «.'» означает транспонирование (не следует путать со знаком «'», который переводит комплексные числа в им сопряженные). Первый элемент матрицы соответствует ЭДС фазы А, второй элемент - ЭДС фазы В,
-заданное фазное напряжение, знак «.'» означает транспонирование (не следует путать со знаком «'», который переводит комплексные числа в им сопряженные). Первый элемент матрицы соответствует ЭДС фазы А, второй элемент - ЭДС фазы В,
отстающей от ЭДС фазы А на угол 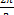 , третий элемент -ЭДС фазы
, третий элемент -ЭДС фазы
С, опережающей ЭДС фазы А на угол 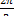 .
.
В данных схемах нет источников тока, поэтому столбцовая матрица 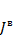 имеет только нулевые элементы и кратко записывается следующим образом:
имеет только нулевые элементы и кратко записывается следующим образом:
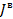 = zeros(7,1).
= zeros(7,1).
Для расчета схемы на ЭВМ необходимо применить программный комплекс MATLAB и в нем использовать сценарий «серуе», разработанный на кафедре электротехники и электроэнергетики ВлГУ.
Необходимо ввести четыре указанные матрицы в ЭВМ, провести расчет токов, напряжений и мощностей, сделать распечатку результатов расчетов и по этой распечатке построить векторную диаграмму токов и топографическую диаграмму напряжений.
Векторная диаграмма токов - это геометрическое представление первого закона Кирхгофа в комплексной форме для любого узла схемы:
 , где k - количество ветвей, присоединенных к данному узлу схемы.
, где k - количество ветвей, присоединенных к данному узлу схемы.
Топографическая диаграмма напряжений — это геометрическое представление второго закона Кирхгофа для любого замкнутого контура схемы:
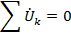
где n - количество ветвей с активными и пассивным» элементами в данном замкнутом контуре.
Рассмотрим пример подобного расчета. Дана схема несимметричной трехфазной цепи с источниками фазных ЭДС, которые на комплексной плоскости образуют симметричную трёхлучевую звезду (рис. 4).
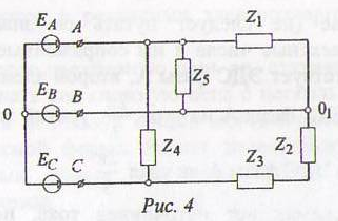
Этой схеме соответствует следующий граф (рис. 5).
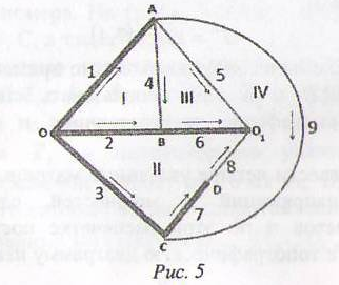
Используем программу MATLAB, сценарий 'серуе':
» серуе
Топологическая матрица В
ТМ=[1 -1 0 1 0 0 0 0 0; 0-11 0 0-1 1 1 0; 0 0 0-1 1 -1 0 0 0; 0 0 0 0-1 0 1 1 1]
сопротивления ветвей
PV=diag([0 0 0 40-60i 60-70i 0 50-70i 55+75i 45+65i])
ЭДС ветвей
SV=660*[1 exp(-2*i*pi/3) exp(2*i*pi/3) 0 0 0 0 0 0].'
источники тока ветвей
CV=zeros(9,1)
Матрица контурных сопротивлений РМ=
1.0е+002 *
0.4000 - 0.6000i 0 -0.4000 + 0.6000i 0
0 1.0500 + 0.0500i 0 1.0500 + 0.0500i
-0.4000 + 0.6000i 0 1.0000 - 1.3000i -0.6000 + 0.7000i
0 1.0500 + 0.0500i -0.6000 + 0.7000i 2.1000
Матрица контурных ЭДС АМ=
1.0е+003 *
0.9900 + 0.5716i
0 + 1.1432i
Матрица контурных токов Х=
4.4850+13.5961i
-0.6663+25.2739i
3.4647-2.2238i
1.1836-14.4114i
Токи ветвей XS=
4.4850+13.5961i
-3.8187-39.8700i
-0.6663+25.2739i
1.0203+15.8198i
2.2811+12.1876i
-2.7984-23.0501i
0.5173+10.8625i
0.5173+10.8625i
1.1836-14.4114i
Напряжения ветвей XC=
1.0e+002*
-6.6000
3.300+5.7158i
3.300-5.7158i
9.9000 + 5.7158i
9.9000 + 5.7158i
0
7.8624 + 5.0692i
-7.8624 + 6.3623i
9.9000 - 5.7158i
Токи пассивных участков ветвей XSP=
4.4850 +13.5961i
-3.8187-38.8700i
-0.6663 +25.2739i
1.0203 +15.8198i
2.2811 +12.1876i
-2.7984 -23.0501i
0.5173 +10.8625i
0.5173 +10.8625i
1.1836-14.4114i
Напряжения пассивных участков ветвей XCP=
1.0е+002 *
0
0
0
9.9000 + 5.7158i
9.9000 + 5.7158i
0
7.8624 + 5.0692i
-7.8624 + 6.3623i
9.9000 - 5.7158i
Мощности ветвей S=
1.0e+004*
-0.2960+0.8973i
-2.3477+1.0644i
-1.4666-0.7960i
1.0052-1.5078i
0.9224-1.0762i
0
0.5913-0.8278i
0.6504+0.8870i
0.9409+1.3591i
Мощности пассивных участков ветвей SPU=
1.0e+004*
0
0
0
1.0052-1.5078i
0.9224-1.0762i
0
0.5913-0.8278i
0.6504+0.8870i
0.9409+1.3591i
Мощности источников ветвей SI=
1.0e+0.004*
0.2960-0.8973i
2.3477-1.0644i
1.4666+0.7960i
0
0
0
0
0
0
>>sum([SPU SI])
Ans=
1.0e+004*
4.1103-1.1658i 4.1103-1.1658i
Уравнение баланса комплексных мощностей имеет вид
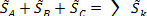
Как видно из результатов расчета, это условие выполняется точно. Суммарная активная мощность источников и приемников составила 41103Вт, а реактивная 11658 Вар.
Построим векторную диаграмму токов и топографическую диаграмму напряжений, используя два пункта из расчета в MATLAB: напряжения ветвей и токи ветвей.
В программном комплексе MatLab существует специальный сценарий для построения векторных диаграмм - vdiagrl. Оператор вводится по следующему правилу: vdiagrl (n,а) для каждого узла, где n - номер фигуры, которая соответствует полной топографической диаграмме напряжений (n = 1) или векторной диаграмме токов (n = 2); а - массив комплексных чисел: первое значение - от какой точки на комплексной плоскости начинать диаграмму; остальные значения - откладываемые комплексные числа; каждый последующий отрезок откладывается от конца предыдущего.
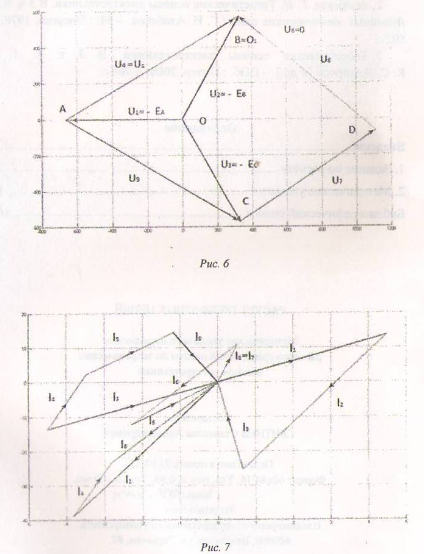
Построим топографическую диаграмму напряжений (рис. 6) по закону Кирхгофа для напряжений, введя следующие команды после завершения основного расчета в MATLAB:
» vdiagrl(1,[0 ХС(1) ХС(4) -X(X2)],’linewidth’,2,’edgecolor’,’flat’) - контур I
» vdiagrl(l,[0 ХС(3) ХС(7) ХС(8) -ХС(6) -XC(2)],’linewidth’,2,’edgecolor’,’flat’) - контур II
» vdiagrl(1,[ХС(1) ХС(5) -ХС(6) -XC(4)],’linewidth’,2,’edgecolor’,’flat’) - контур III
» vdiagrl (1,[ХС(1) ХС(9) ХС(7) ХС(8) –XC(5)],’linewidth’,2,’edgecolor’,’flat’) - контур IV
Команду vdiagrl(l,a) необходимо ввести (в - у + 1) раз; в - число ветвей схемы, у - число узлов схемы.
Для того чтобы построить векторную диаграмму токов (рис. 7), необходимо ввести следующую последовательность команд в соответствии с законом Кирхгофа для токов:
» vdiagrl(2,[0 -XS(1) XS(4) XS(5) XS(9)],’linewidth’,2,’edgecolor’,’flat’) -узел A
» vdiagrl(2,[0 - XS(2) - XS(4) XS(6)],’linewidth’,2,’edgecolor’,’flat’) -узел В
» vdiagrl (2,[0 XS(1) XS(2) XS(3)],’linewidth’,2,’edgecolor’,’flat’) -узел О
» vdiagrl (2,[0 -XS(5) -XS(6) -XS(8)],’linewidth’,2,’edgecoIor’,’flat’) - узел 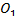
Команду vdiagrl(2,a) необходимо ввести (у - 1) раз. Учтём, что 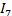 =
= 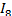 позволяет нам не записывать команду для узла D.
позволяет нам не записывать команду для узла D.
Библиографический список
1. Теоретические основы электротехники. В 2 т. Т. 1 / под ред. П. А. Ионкина. - М.: Высш. шк., 1978. - 592 с.
2. Атабеков, Г. И. Теоретические основы электротехники. В 3 ч. 4.1. Линейные электрические цепи / Г. И. Атабеков. - М. : Энергия, 1978. - 592 с.
3. Теоретические основы электротехники. В 3 т. Т. 1 / К. С. Демирчян [и др.]. - СПб.: Питер, 2006. - 464 с.
Дата добавления: 2016-12-27; просмотров: 1925;











