СОЕДИНЕНИЯ ОБМОТОК ГЕНЕРАТОРА
На рис. 65 показана схема генератора, у которого имеются три независимые однофазные цепи. Э.д.с. в этих цепях одинаковы, имеют одинаковые амплитуды и сдвинуты по фазе на 1/3 периода. К каждой паре зажимов обмотки статора генератора можно подключить провода, подводящие ток к нагрузке. Эти три фазы выгоднее объединить в одну общую трехфазную систему. Для этого обмотки генератора соединяют между собой звездой или треугольником.
При соединении обмоток генератора звездой (рис. 66) концы всех трех фаз X, Y и Z (или начала A, В и С) соединяются между собой, а от начала (или концов) выводятся провода, отводящие энергию в сеть. Полученные таким образом три провода называются линейными, а напряжение между любыми двумя линейными проводами — линейными напряжениями Uл. От общей точки соединений концов (или начал) трех фаз (от нулевой точки звезды) может
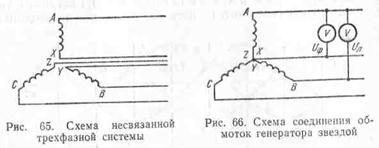
быть отведен четвертый провод, называемый нулевым. Напряжение между любым из трех линейных проводов и нулевым проводом равно напряжению между началом и концом одной фазы, т. е. фазному напряжению Uф.
Обычно все фазы обмотки генератора выполняют одинаковыми так, что действующие значения э. д. с. в фазах равны, т. е. ЕA= ЕB=ЕC. Если в цепь каждой фазы генератора включить нагрузку,
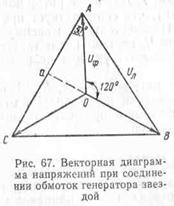
то по этим цепям будут протекать токи. В случае одинакового по величине и характеру сопротивления всех трех фаз приемника, т. е. при равномерной нагрузке, токи в фазах равны по силе и сдвинуты по фазе относительно своих напряжений на один и тот же угол . Как максимальные, так и действующие значения фазных напряжений при равномерной нагрузке равны, т. е. UA= UB=UC. Эти напряжения сдвинуты по фазе на 120°, как показана на векторной диаграмме (рис. 67). Напряжение между любыми точками схемы (см. рис. 66) соответствует векторам (рис. 67) между теми же точками. Так, например, напряжение между точками A и О схемы (фазное напряжение UА) соответствует вектору A-O диаграммы, а напряжение между линейными проводами А и В схемы — вектору линейного напряжения АВ диаграммы. По векторной диаграмме легко установить соотношение между линейным и фазным напряжением. Из треугольника АОа можно записать следующее соотношение:

откуда
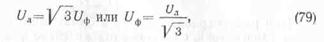
т, е. при соединении обмоток генератора звездой линейное напряжение в 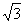 = 1,73 раза больше фазного (при равномерной нагрузке).
= 1,73 раза больше фазного (при равномерной нагрузке).
Из схемы (см. рис. 66) видно, что при соединении обмоток генератора звездой ток в линейном проводе равен току в фазах генератора, т. е. Iл=Iф.
На основании первого закона Кирхгофа можем записать, что ток в нулевом проводе равен геометрической сумме токов в фазах генератора, т. е.
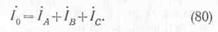
При равномерной нагрузке токи в фазах генератора равны между собой и сдвинуты по фазе на 1/3 периода. Геометрическая сумма токов трех фаз в этом случае равна нулю, т. е. в нулевом проводе тока не будет. Поэтому при симметричной нагрузке нулевой провод может отсутствовать. При несимметричной нагрузке ток в нулевом проводе не равен нулю, но обычно нулевой провод имеет меньшее поперечное сечение, чем линейные.
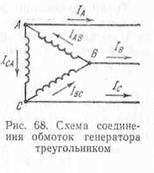
При соединении обмоток генератора треугольником (рис. 68) начало (или конец) каждой фазы соединяется с концом (или началом) другой фазы. Таким образом, три фазы генератора образуют замкнутый контур, в котором действует э. д. с, равная геометрической сумме э. д. с, индуктированных в фазах генератора, т. е. Еа+Ев +Ес. Так как э. д. с. в фазах генератора равны и сдвинуты
на 1/3 периода по фазе, то геометрическая сумма их равна нулю и, следовательно, в замкнутом контуре трехфазной системы, соединенной треугольником, никакого тока при отсутствии внешней нагрузки не будет.
Линейные провода при соединении треугольником подключаются к точкам соединения начала одной фазы и конца другой. Напряжение между линейными проводами равно напряжению между началом и концом одной фазы Таким образом при соединении обмоток генератора треугольником линейное напряжение равно фазному, т. е.
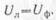
При равномерной нагрузке в фазах обмоток генератора протекают равные токи, сдвинутые относительно фазных напряжений на одинаковые углы , т. е. IAB = IBC=ICA
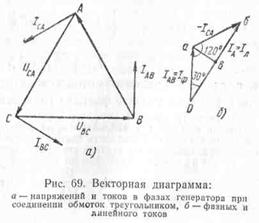
На рис. 69, а изображена векторная диаграмма, на которой показаны векторы фазных напряжений и токов.
Точки соединений фаз и линейных проводов А, В и С являются точками разветвления, и линейные токи не равны фазным. Приняв за положительное направление фазных и линейных токов, указанное на рис. 69, на основании первого закона Кирхгофа для мгновенных значений токов можно написать следующие выражения:
iA= iAB- iCA; iB= iBC- iAB; iC= iCA- iBC
Так как токи синусоидальны, то заменим алгебраическое вычитание мгновенных значений токов геометрическим вычитанием векторов, изображающих их действующие значения:
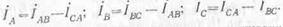
Ток линейного провода АIА определится геометрической разностью: векторов фазных токов IAB и ICA.
Для построения вектора линейного тока IA изобразим вектор фазного тока IAB (рис. 69,6), из конца которого построим вектор -ICA, равный и противоположно направленный вектору ICA. Вектор, соединяющий начало вектора IAB с концом вектора -ICA, является вектором линейного тока IA Аналогично могут быть построены векторы линейных токов IB и IC.
Из векторной диаграммы (рис. 69, б) легко вывести соотношение между линейными и фазными токами при соединении обмоток генератора треугольником. Из треугольника оаб можно записать: 
откуда
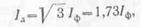
т. е. присоединении обмоток генератора треугольником линейный ток в 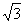 раза больше фазного (при равномерной нагрузке).
раза больше фазного (при равномерной нагрузке).
Пример. Трехфазный генератор переменного тока, обмотка статора которого соединена звездой, при полной нагрузке имеет линейное напряжение 220 в при линейном токе 10 а. Определить линейное напряжение и ток при полной нагрузке генератора, если обмотка статора его будет соединена треугольником.
Решение. Фазное напряжение генератора
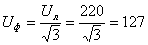 в
в
и фазный ток Iф =Iл=10 а.
При соединении обмотки генератора треугольником линейное напряжение равно фазному, т. е.
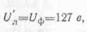
а линейный ток в 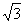 раз больше фазного, т. е.
раз больше фазного, т. е.
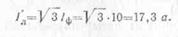

Дата добавления: 2021-04-21; просмотров: 529;











