ФАЗОВЫЕ ПЕРЕХОДЫ В НЕФТИ, ВОДЕ И ГАЗЕ

Фазовые переходы подчиняются определённым закономерностям, в основе которых лежит понятие равновесия фаз. Равновесие фаз характеризуется константой равновесия, которая зависит от температуры и давления.

Константа фазового равновесия i-го компонента характеризуется отношением мольной доли компонента в газовой фазе (у_i или N_yi) к мольной доле этого компонента в жидкой фазе (х_i или N_xi), находящейся в равновесном состоянии с газовой фазой:

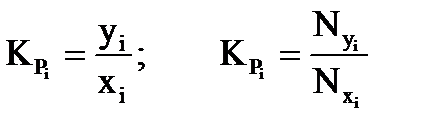. (3.1)

Для определения равновесного состояния газожидкостных смесей используются законы Дальтона и Рауля.

Согласно закону Дальтона каждый компонент, входящий в газовую фазу имеет своё парциальное давление P_i, а общее давление в газовой системе равно сумме парциальных давлений:

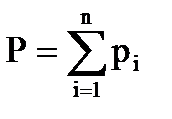(3.2)

Согласно закону Рауля, парциальное давление компонента над жидкостью (нефтью) равно давлению насыщенного пара (Р_{нас. пара}) или упругости пара (Q_i) и этого компонента, умноженному на его мольную долю в нефти:

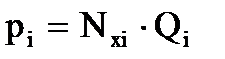или 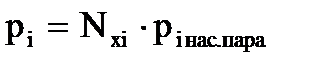, (3.3)

где Q_i – упругость паров компонента;

N_xi – мольная доля компонента;

p_{iнас. пара} – давление насыщенного пара i-го компонента.

В момент равновесия парциальное давление i-го компонента в газовой фазе равно парциальному давлению компонента над жидкостью. И это описывается законом Дальтона-Рауля для равновесного состояния газовой и нефтяной фазы:

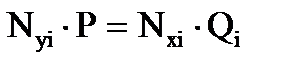; (3.4)

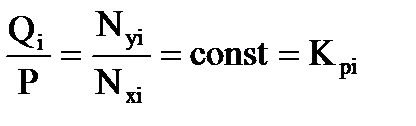, (3.5)

где К_i – константа равновесия i-го компонента при данной температуре и давлении смеси.

Оценить состав газовой (N_yi) и жидкой (N_xi) фаз можно на основе уравнения материального баланса, записанного для одного моля нефтегазовой смеси (N_zi):

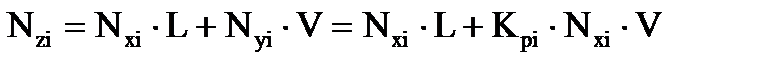, (3.6)

где L – мольная доля жидкой фазы;

V – мольная доля паровой фазы;

N_zi – мольные доли компонентов в нефтегазовой смеси.

По условию сумма мольной доли жидкой и паровой фаз равна единице. Отсюда:

V=1–L. (3.7)

Используя уравнения (3.6) и (3.7) получим выражение для мольной доли компонента жидкой фазы:

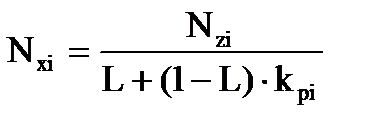, (3.8)

или

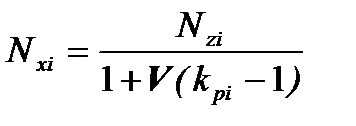, (3.9)

и для мольной доли компонента газовой фазы:

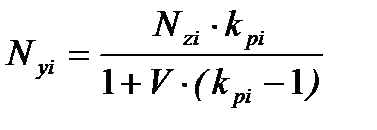. (3.10)

Величины: V и L оцениваются и уточняются методом последовательных проб и приближений (см. разд. "Практикум для самостоятельной работы"). .