Уравнения импульсных систем управления

С помощью структурной схемы, приведенной на рис. 15.8, можно получить различные уравнения импульсной системы, используя уравнения импульсного элемента и непрерывной части, представленные в той или иной форме.

Предположим, ИЭ формирует прямоугольные импульсы длительностью 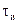с различной амплитудой. График его выходного сигнала 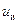для этого случая приведен на рис. 15.9. Аналитически зависимость, представленную на рис. 15.9, можно описать следующими выражениями:

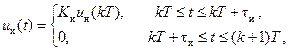(15.3)

где 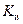– коэффициент передачи ИЭ.

Предположим, непрерывная часть (НЧ) (см. рис. 15.8) задана своими уравнениями в переменных состояния

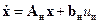, (15.4)

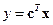. (15.5)

Обратим внимание, что в импульсных системах всегда отсутствует прямая связь между входной переменной 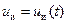непрерывной части и её выходной переменной 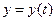. Поэтому в уравнении (15.5) отсутствует переменная 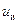. Кроме того, в импульсных системах (см. рис. 15.8) связь между входной переменной 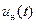и выходной непрерывной переменной 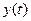является нелинейной. Поэтому чаще всего здесь рассматривается связь между дискретными значениями 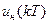управления 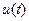, дискретными значениями 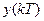выходной переменной 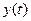и соответствующими значениями переменных состояния НЧ.

Для вывода уравнений импульсной системы в разомкнутом состоянии (см. рис. 15.8) воспользуемся формулой Коши. На основе уравнения (15.4) можно записать равенство

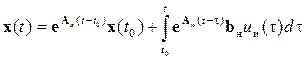. (15.6)

Положим в (15.6) 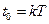, , 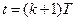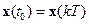и проведём замену переменных. В результате будем иметь

.

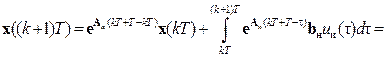
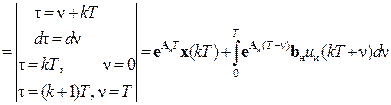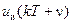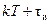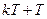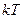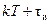В соответствии с уравнениями (15.3) импульсного элемента величина на интервале от до равна нулю, а на интервале от до равна 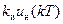. Поэтому

.

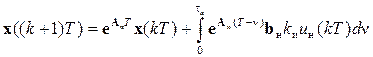Отсюда следует равенство

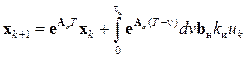, (15.7)

где обозначено 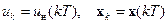. Выражения (15.7) и (15.5) можно записать следующим образом:

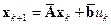, (15.8)

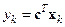, (15.9)

где

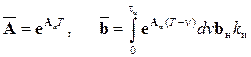. (15.10)

Если матрица 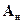является неособенной, т.е. 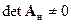, то интеграл в (15.10) можно взять в символьной форме. В результате получим

.

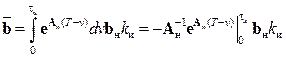Отсюда

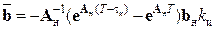. (15.11)

Если же матрица 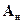является особенной, т.е. 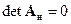, то интеграл в (15.10) необходимо вычислять путем интегрирования каждого элемента подынтегральной матрицы в отдельности.

Выражения (15.8), (15.9) являются разностными уравнениями импульсной системы в разомкнутом состоянии. Эти уравнения связывают лишь дискретные значения переменных состояния с дискретными же значениями входной переменной 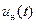и выходной переменной 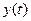рассматриваемой системы (см. рис. 15.8). Название «разностные уравнения» связаны с тем, что в эти уравнения можно ввести первые разности, т.е. величины 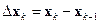– убывающую разность, или же 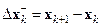– восходящую разность.

Для вывода уравнений замкнутой системы, структурная схема которой показана на рис. 15.10, необходимо в уравнении (15.8) заменить 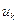на 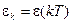и учесть, что 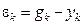. В результате, принимая во внимание уравнение (15.9), получим

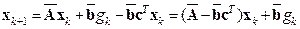
или

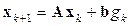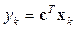, , (15.12)

где

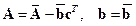. (15.13)

Выражения (15.12) являются разностными уравнениями в переменных состояния замкнутой импульсной или цифровой системы.

Таким образом, и импульсные, и цифровые системы описываются разностными уравнениями в переменных состояния типа (15.12), (15.13), решениями которых являются дискретные функции 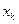, 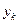. Поэтому, когда говорят о дискретных системах, то имеют в виду и импульсные, и цифровые системы.

Пример 15.1.Найти уравнения импульсной системы, структурная схема которой приведена на рис. 15.10. Импульсный элемент формирует прямоугольные импульсы с параметрами 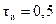с, 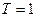с. Его коэффициент передачи 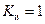. Непрерывная часть описывается уравнениями:

.

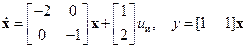Решение.В данном случае матрица 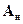является диагональной, поэтому в соответствии с выражениями (15.8) – (15.11) имеем

, ,

, ,

.

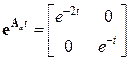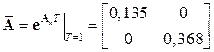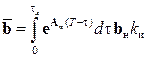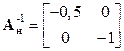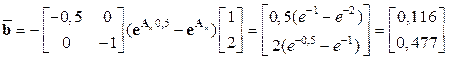Итак, уравнения системы в разомкнутом состоянии имеют вид

.

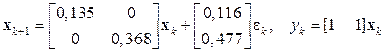Перейдем к выводу уравнений системы в замкнутом состоянии. По формуле (15.13) находим:

.

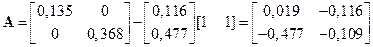Следовательно, согласно (15.12), в замкнутом состоянии рассматриваемая система

описывается уравнениями:

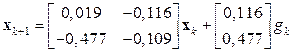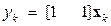, . (15.14)

Заметим, что вектор с в полученном уравнении выхода совпадает с аналогичным вектором непрерывной части системы.

Коэффициенты матрицы 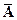и вектора 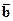(15.10) из уравнения (15.8) системы в разомкнутом состоянии удобно находить с помощью MATLAB. При этом, если импульсный элемент формирует прямоугольные импульсы, длительность которых меньше периода следования, т.е. 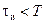, то можно использовать нестандартную программу c2taud, текст которой приведён в приложении П.4. Если же длительность импульсов равна периоду следования, т.е. 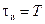, и 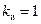, то используется стандартная программа c2d. Отметим также, что в MATLAB уравнение выходов (15.5) принимается в виде .

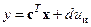Решение в MATLAB. В рассматриваемом примере 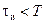, , 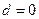поэтому обращение к MATLAB имеет вид:

% команды

sys = ss([-2 0;0 -1],[1 2]',[1 1],0);

T =1; tau = 0.5; kie = 1;

[syss, sysw] = c2taud(sys,T,tau,kie);

[a,b,c,d]=ssdata(syss)

% результат

a =

0.13534 0

0 0.36788

b =

0.11627

0.4773

c =

1 1

d =

Полученные в MATLAB результаты, очевидно, полностью соответствуют приведённым выше. ■

Если непрерывная часть системы (рис. 15.10) задана не уравнениями в переменных состояния, а передаточной функцией (в рассмотренном примере она равна (3p + 5)/(p² + 3p + 2), то в приведенных выше командах пакета MATLAB первая имеет вид

sys = tf([3 5],[1 3 2]);

а остальные команды не меняются. Пример применения программы c2d для получения уравнений импульсной системы по модели непрерывной части приведён ниже.

Уравнения вход-выход дискретных систем управления. Преобразование Лапласа над решетчатыми функциями, которые в соответствии с полученными выше уравнениями описывают поведение дискретных систем, называется дискретным преобразованием Лапласа или Z-преобразованием. Результат Z-преобразования решетчатой функции, как и в случае непрерывного преобразования Лапласа, называется изображением, а сама решетчатая функция – оригиналом.

Для наиболее распространенных функций z-изображения приведены в приложении П.1. Для существования Z-преобразования решетчатая функция должна быть равна нулю при отрицательном значении аргумента, а при 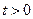расти не быстрее экспоненты.

Укажем некоторые свойства Z-преобразования. Пусть 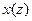результат Z-преобразования некоторой дискретной функции 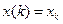, т. е. 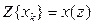. Тогда справедливы соотношения

, , ,

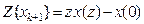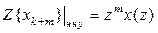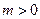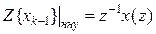(15.15)

и теоремы о предельных значениях

,

.

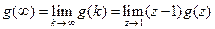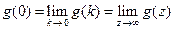Здесь 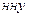– обозначение нулевых начальных условий.

Соотношения (15.15) применяются для определения реакции замкнутых систем на заданные воздействия, если известны z-изображения последних. Z-преобразование позволяет ввести, как и в непрерывном случае, передаточные функции дискретных систем.

Если воспользоваться соотношениями (15.15) и преобразовать уравнения (15.14) при нулевых начальных условиях, то будем иметь

, .

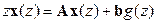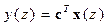Отсюда

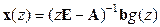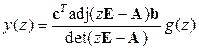, . (15.16)

Применяя правила обратного Z-преобразования к правым частям равенств (15.16), можно найти оригиналы 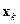и 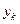при заданном 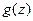. Это позволяет получить аналитические выражения, которые определяют значения 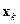и 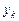для любого значения .

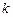Замечание. При взятии обратного Z-преобразования от изображения в виде рациональной дроби типа (5.16) на сумму простейших дробей разлагается не само z-изображение искомой функции, а сначала из числителя z-изображения выносится переменная z. Оставшаяся рациональная дробь разлагается обычным путем на сумму простейших дробей. Эта особенность связана с тем, что z-изображения всегда имеют множитель z в числителе.

Из второго соотношения (15.16) можно также найти передаточную функцию замкнутой дискретной системы (15.14):

,

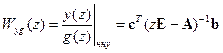или

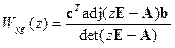. (15.17)

Таким образом, передаточные функции импульсных систем, как и передаточные функции непрерывных систем, являются отношением полиномов, но от переменной 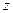. При этом степень числителя также не может превышать степень знаменателя.

Если уравнения (15.8), (15.9) подвергнутьZ-преобразованию, то при 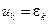можно получить передаточную функцию 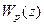импульсной системы в разомкнутом состоянии, тоже как отношение полиномов от z. При этом передаточная функция импульсной системы в замкнутом состоянии при отрицательной единичной обратной связи определяется по обычной формуле, т.е. если

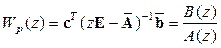, то 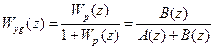. (15.18)

Пример 15.2. Порядок определения передаточных функций и соответствующих уравнений «вход-выход» в MATLAB покажем на примере системы (15.14).

% Вводим заданные матрицы, векторы и число d=0 командами:

a = [0.019 -0.116;-0.477 -0.109];

b = [0.116 0.477]';

c = [1 1]; d = [0];

[ap,bp] = ss2tf(a,b,c,d)

% результат:

bp =

0 0.593 -0.10708

ap =

1 0.09 -0.057403

Следовательно, дискретная передаточная функция системы (15.14)

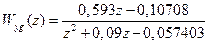. (15.19)

Чтобы перейти от передаточной функции (15.19) к уравнению «вход-выход» разделим числитель и знаменатель на z в старшей степени (в данном случае на z²) и запишем, в соответствии с определением передаточных функций, пропорцию

.

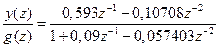Раскрывая эту пропорцию и переходя к оригиналам с помощью соотношений (15.15), получим

.

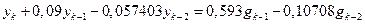Это выражение и является разностным уравнением «вход-выход» импульсной системы, рассмотренной в примере 15.1. ■

Отметим в заключение этого параграфа, что приведённые соотношения (15.8) – (15.18) позволяют найти модель импульсной системы по уравнению импульсного элемента (15.3) и по уравнениям в переменных состояния её непрерывной части (15.4), (15.5).