Управляемая форма Жордана
Система линейных дифференциальных уравнений в переменных состояния, где матрица A системы является сопровождающей, а входной вектор управления b равен n-му столбцу единичной матрицы (например, система (7.8)) называется канонической управляемой формой или управляемой формой Фробениуса. Как показано выше, если уравнения некоторого объекта приведены к этой форме, то легко синтезируется, в частности, модальное управление.
Если к управляемой форме Фробениуса (7.8) привести уравнения нелинейных управляемых систем, например (14.15), то их коэффициенты чаще всего оказываются зависящими от управления и его производных по времени: 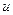 ,
, 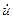 ,
, 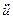 и т.д. Это значительно осложняет синтез нелинейных САУ на основе этого подхода, делая его практически невозможным.
и т.д. Это значительно осложняет синтез нелинейных САУ на основе этого подхода, делая его практически невозможным.
В то же время существует другая форма уравнений динамических систем в переменных состояния, которая также позволяет сравнительно легко, действуя по формальному алгоритму, найти, нелинейное управление, например, оптимальное или аналогичное модальному в линейном случае. При этом управлении матрица уравнений замкнутой нелинейной системы в квазилинейном представлении типа (14.17) и при соответствующих переменных состояния имеет вид 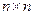 -клетки Жордана (в общем случае с различными диагональными элементами). Поэтому эта форма и называется управляемой формой Жордана.
-клетки Жордана (в общем случае с различными диагональными элементами). Поэтому эта форма и называется управляемой формой Жордана.
Переходя к определению управляемой формы Жордана, рассмотрим следующую систему уравнений:
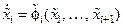 ,
, 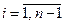 , (14.26)
, (14.26)
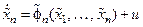 , (14.27)
, (14.27)
где 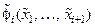 и
и 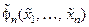 – нелинейные функции переменных состояния
– нелинейные функции переменных состояния 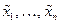 , дифференцируемые необходимое число раз по всем своим переменным; u – управление.
, дифференцируемые необходимое число раз по всем своим переменным; u – управление.
Предположим, система уравнений (14.26), (14.27) удовлетворяет следующим условиям:
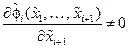 ,
, 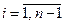 ,
, 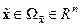 , (14.28)
, (14.28)
где 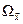 – некоторая область пространства
– некоторая область пространства 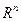 . Условимся, что здесь и в дальнейшем имеются в виду только такие области пространства Rn, которые включают начало соответствующей системы координат:
. Условимся, что здесь и в дальнейшем имеются в виду только такие области пространства Rn, которые включают начало соответствующей системы координат: 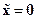 ,
, 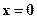 и т.д.
и т.д.
Определение. Если нелинейности системы уравнений (14.26), (14.27) удовлетворяют условиям (14.28), то эта система уравнений называется управляемой формой Жорданa.■
Сравнивая уравнения (7.8) и (14.26), (14.27), нетрудно заключить, что каноническая управляемая форма Фробениуса является частным случаем управляемой формы Жордана (УФЖ), при 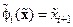 ,
, 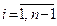 (для
(для 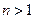 ) и
) и 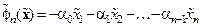 .
.
Переменные состояния 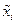 ,
, 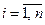 в дальнейшем будем считать доступными прямому измерению отклонениями от положения равновесия
в дальнейшем будем считать доступными прямому измерению отклонениями от положения равновесия 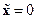 , причем
, причем 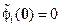 ,
, 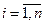 .
.
Задача синтеза САУ для объекта (14.26), (14.27) заключается в определении такого управления 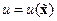 , при котором обеспечивается асимптотическая устойчивость в большом или в целом положения равновесия
, при котором обеспечивается асимптотическая устойчивость в большом или в целом положения равновесия 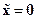 .
.
С целью построения искомого управления 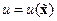 задаются n вещественными числами
задаются n вещественными числами 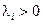 ,
, 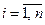 и вводят новые переменные состояния wi замкнутой системы следующим образом:
и вводят новые переменные состояния wi замкнутой системы следующим образом:
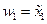 ,
, 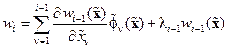 ,
, 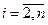 . (14.29)
. (14.29)
Далее определяются функции 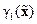 и
и 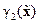 в соответствии с формулами:
в соответствии с формулами:
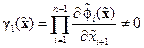 ,
, 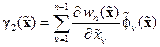 , (14. 30)
, (14. 30)
где 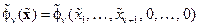 .
.
Из выражений (14.29) следует, что каждая переменная wi зависит лишь от первых i
переменных состояния 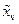 ,
, 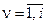 исходного объекта (14.26), (14.27), т.е.
исходного объекта (14.26), (14.27), т.е. 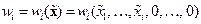 . Введённые функции wi,
. Введённые функции wi, 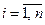 ,
, 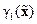 и
и 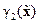 позволяют сформулировать теорему, которая доставляет решение поставленной выше задачи синтеза.
позволяют сформулировать теорему, которая доставляет решение поставленной выше задачи синтеза.
Теорема 14.2. Если правые части системы (14.26), (14.27) удовлетворяют в некоторой области 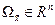 условиям (14.28), а управление
условиям (14.28), а управление 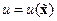 определяется выражением
определяется выражением
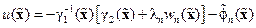 , (14.31)
, (14.31)
то переменные 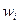 (14.29) удовлетворяют системе уравнений
(14.29) удовлетворяют системе уравнений
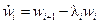 ,
, 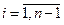 ,
, 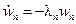 . ■ (14.32)
. ■ (14.32)
Доказательство теоремы достаточно очевидно из соотношений (14.26) – (14.31) и здесь не приводится. Заметим только, что при выполнении условий (14.28) функция 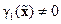 . Тем самым обеспечивается существование стабилизирующего управления
. Тем самым обеспечивается существование стабилизирующего управления 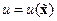 (14.31). В векторно-матричной форме уравнения (14.32) имеют вид
(14.31). В векторно-матричной форме уравнения (14.32) имеют вид
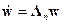 , (14.33)
, (14.33)
где
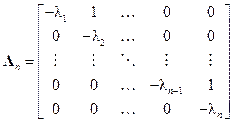 .
.
При 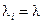 ,
, 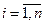 матрица
матрица 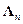 совпадает с клеткой Жордана размера
совпадает с клеткой Жордана размера 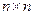 . Именно поэтому система уравнений (14.26), (14.27) называется управляемой формой Жордана, если её
. Именно поэтому система уравнений (14.26), (14.27) называется управляемой формой Жордана, если её
правые части удовлетворяют условиям (14.28) в некоторой области 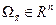 .
.
Систему уравнений (14.26), (14.27) с учетом управления (14.31) можно записать в виде
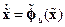 , (14.34)
, (14.34)
где 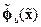 – нелинейная вектор-функция, причем
– нелинейная вектор-функция, причем 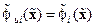 ,
, 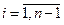 , а
, а 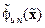 определяется правыми частями соотношений (14.27) и (14.29) – (14.31).
определяется правыми частями соотношений (14.27) и (14.29) – (14.31).
Покажем, что положение равновесия системы (14.34) асимптотически устойчиво и имеет некоторую непустую область притяжения 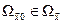 . Действительно, согласно равенствам (14.29), вектор-функция
. Действительно, согласно равенствам (14.29), вектор-функция 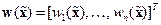 является дифференцируемой по всем своим переменным, поэтому с учетом уравнения (14.34) можно записать равенство
является дифференцируемой по всем своим переменным, поэтому с учетом уравнения (14.34) можно записать равенство
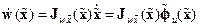 , (14.35)
, (14.35)
где 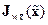 – якобиан вектор-функции
– якобиан вектор-функции 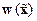 по переменным
по переменным 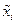 .
.
Нетрудно установить, что в силу свойств функций 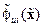 ,
, 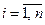 и условий (14.28) существует область
и условий (14.28) существует область 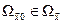 такая, что
такая, что
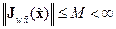 ,
, 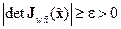 ,
, 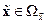 , (14.36)
, (14.36)
причем при 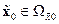 , и всех
, и всех 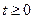 решение
решение 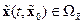 , а в области
, а в области 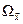 существует обратное отображение
существует обратное отображение 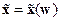 . Поэтому если в уравнение (14.35) подставить зависимость
. Поэтому если в уравнение (14.35) подставить зависимость 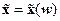 , то оно перейдёт в (14.33). Приравнивая правые части этих уравнений, придём к равенству
, то оно перейдёт в (14.33). Приравнивая правые части этих уравнений, придём к равенству

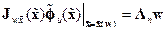 ,
, 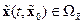 ,
, 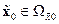 . (14.37)
. (14.37)
Далее рассмотрим функцию 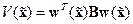 , где B – симметрическая матрица, определяемая решением уравнения Ляпунова
, где B – симметрическая матрица, определяемая решением уравнения Ляпунова
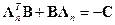 (14.38)
(14.38)
при 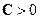 . Поскольку
. Поскольку 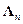 – устойчивая матрица, то
– устойчивая матрица, то 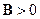 , поэтому функция
, поэтому функция 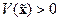 тоже.
тоже.
Её производная по времени как сложной функции определяется следующим выражением:
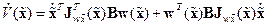 ,
, 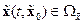 .
.
Отсюда с учетом равенств (14.34) выводим
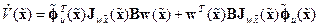 .
.
Наконец, комбинируя это выражение с равенством (14.37) и учитывая (14.38), получим
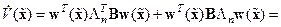
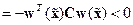 ,
, 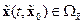 .
.
В силу приведённой выше теоремы 12.4 это неравенство доказывает асимптотическую устойчивость положения равновесия 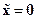 замкнутой системы (14.34) и то, что область
замкнутой системы (14.34) и то, что область 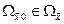 является его областью притяжения, так как по условию
является его областью притяжения, так как по условию 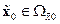 .
.
Итак, если уравнения некоторого объекта имеют УФЖ (14.26) – (14.28), то соотношения (14.29) – (14.31) позволяют найти стабилизирующее управление 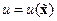 в виде нелинейной обратной связи по вектору состояния
в виде нелинейной обратной связи по вектору состояния 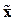 .
.
Дата добавления: 2022-05-27; просмотров: 74;










