Приведение уравнений объектов к УФЖ
В общем случае уравнения объектов управления по форме не соответствуют уравнениям УФЖ (14.26) – (14.28). Поэтому для построения управления по формулам (14.29) – (14.31) необходимо предварительно привести их к УФЖ. Рассмотрим подробнее порядок приведения уравнений некоторых объектов к этой форме.
Постоянный вектор 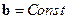 . Предположим, уравнения некоторого объекта n-го порядка имеют вид
. Предположим, уравнения некоторого объекта n-го порядка имеют вид
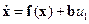 ,
, 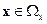 , (14.39)
, (14.39)
где 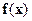 – дифференцируемая не менее
– дифференцируемая не менее 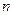 раз вектор-функция.
раз вектор-функция.
Будем считать, что уравнение (14.39) не соответствует УФЖ, и без ограничения общности примем, что 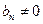 (в противном случае переменные переобозначаются). Это позволяет ввести преобразование
(в противном случае переменные переобозначаются). Это позволяет ввести преобразование
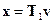 ,
, 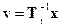 , (14.40)
, (14.40)
где 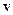 – новый вектор переменных, а
– новый вектор переменных, а
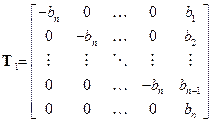 ,
, 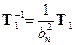 .
.
Преобразование (14.40) приводит уравнение (14.39) к виду 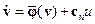 , где
, где 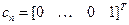 . Эта система имеет УФЖ лишь в некоторых частных случаях. Поэтому чаще всего требуется дополнительное преобразование переменных
. Эта система имеет УФЖ лишь в некоторых частных случаях. Поэтому чаще всего требуется дополнительное преобразование переменных 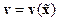 .
.
Ограничимся далее случаем 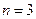 и введём обозначения
и введём обозначения 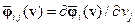 . Тогда если
. Тогда если 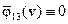 ,
,  и
и 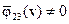 , в некоторой области
, в некоторой области 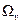 , то полагают
, то полагают 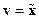 , а если
, а если 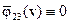 , а
, а 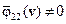 и
и 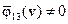 в некоторой области
в некоторой области 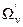 , то полагают
, то полагают 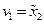 ,
, 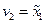 ,
,  . В результате относительно вектора
. В результате относительно вектора 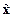 уравнения объекта оказываются в УФЖ.
уравнения объекта оказываются в УФЖ.
Если же 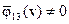 и
и 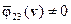 , то используется дополнительное преобразование
, то используется дополнительное преобразование 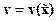 вида
вида 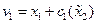 ,
, 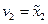 ,
,  . При этом функция
. При этом функция 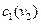 определяется решением дифференциального уравнения
определяется решением дифференциального уравнения
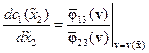 (14.41)
(14.41)
при 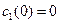 . Здесь предполагается, что решение уравнения (14.41) зависит только от переменной
. Здесь предполагается, что решение уравнения (14.41) зависит только от переменной 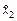 , что приводит, естественно, к некоторым ограничениям рассматриваемого метода синтеза нелинейных САУ для объектов типа (14.39).
, что приводит, естественно, к некоторым ограничениям рассматриваемого метода синтеза нелинейных САУ для объектов типа (14.39).
Тем не менее, на практике достаточно часто встречаются объекты, уравнения которых приводятся к УФЖ указанным преобразованием. В общем случае можно ввести преобразование 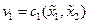 ,
, 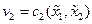 ,
,  . При этом условия
. При этом условия 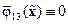 и
и 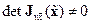 при
при 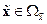 приводят к уравнениям в частных производных, которые позволяют найти
приводят к уравнениям в частных производных, которые позволяют найти 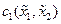 и
и 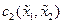 . Аналогичным образом могут быть приведены к УФЖ уравнения объектов других типов с постоянным вектором входа
. Аналогичным образом могут быть приведены к УФЖ уравнения объектов других типов с постоянным вектором входа 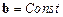 , а затем синтезировано стабилизирующее управление.
, а затем синтезировано стабилизирующее управление.
Переменный вектор 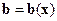 . Ограничимся здесь рассмотрением методики приведения к УФЖ уравнений (14.39) нелинейных объектов второго порядка с переменным вектором входа, т.е. с вектором
. Ограничимся здесь рассмотрением методики приведения к УФЖ уравнений (14.39) нелинейных объектов второго порядка с переменным вектором входа, т.е. с вектором 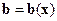 . При этом по тем же причинам, что и выше будем предполагать, что в некоторой области
. При этом по тем же причинам, что и выше будем предполагать, что в некоторой области 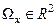 выполняются условия
выполняются условия 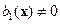 и
и 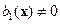 , и, кроме того, эти функции являются дифференцируемыми.
, и, кроме того, эти функции являются дифференцируемыми.
Установлено, что взаимообратные преобразования 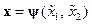 и
и 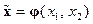 , которые приводят уравнение (14.39) второго порядка к УФЖ, существуют, если выполняется следующее условие:
, которые приводят уравнение (14.39) второго порядка к УФЖ, существуют, если выполняется следующее условие:
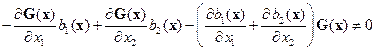 , (14.42)
, (14.42)
где 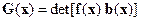 ,
, 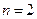 .
.
Если условие (14.42) выполняется, то для построения, например, преобразования 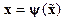 относительно новых переменных
относительно новых переменных 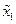 и
и 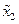 , по аналогии с матрицей Т1 из (14.40), можно полагать
, по аналогии с матрицей Т1 из (14.40), можно полагать
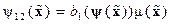 ,
, 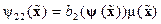 ,
, 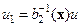 , (14.43)
, (14.43)
где 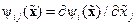 ,
, 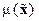 – некоторый интегрирующий множитель, а
– некоторый интегрирующий множитель, а 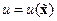 – новое управление. Проинтегрировав уравнения (14.43) и выбрав постоянные интегрирования по условиям
– новое управление. Проинтегрировав уравнения (14.43) и выбрав постоянные интегрирования по условиям 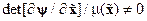 и
и 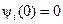 , найдём искомое преобразование
, найдём искомое преобразование 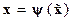 , которое приводит заданное уравнение (14.39) при
, которое приводит заданное уравнение (14.39) при 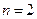 и
и 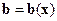 к УФЖ.
к УФЖ.
Для построения обратного преобразования 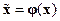 при выполнении условия (14.42) полагают
при выполнении условия (14.42) полагают
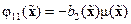 ,
, 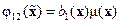 ,
, 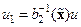 . (14.44)
. (14.44)
В результате интегрирования этих уравнений с учётом условий 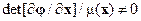 и
и 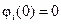 находится преобразование
находится преобразование 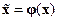 , которое приводит уравнение (14.39) к УФЖ.
, которое приводит уравнение (14.39) к УФЖ.
Условия существования и методика построения преобразований 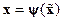 или
или 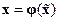 , приводящих к УФЖ уравнения произвольных нелинейных объектов управления общего вида пока не известны.
, приводящих к УФЖ уравнения произвольных нелинейных объектов управления общего вида пока не известны.
Дата добавления: 2022-05-27; просмотров: 174;











