Синтез гурвицевых систем на основе квазилинейной модели

Синтез нелинейных систем управления удобно выполнять, если предварительно математическую модель нелинейного объекта управления представить в квазилинейной форме. Это позволяет, практически без изменений, применять полиномиальный подход, изложенный применительно к линейным системам в седьмой и в восьмой главах.

Рассмотрим нелинейный объект управления, который описывается уравнением

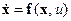, (14.13)

где 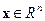– доступный измерению вектор состояния системы; 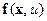– непрерывная дифференцируемая вектор-функция, причем

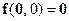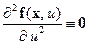, (14.14)

при всех 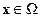. Здесь 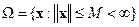– некоторая область пространства 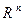. В этих условиях уравнение (14.13) можно заменить квазилинейной моделью вида

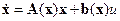, (14.15)

где 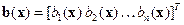и – функциональные n-вектор и непрерывная 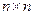-матрица, элементы которых определяются выражениями:

, ,

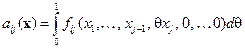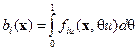где 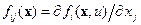, , 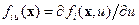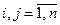; Т – символ операции транспонирования. Предположим также, что выполняется условие

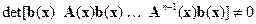. (14.16)

Управление ищется в виде 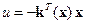. Поэтому с учетом (14.15) уравнение замкнутой системы принимает вид

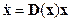, (14.17)

где

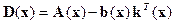. (14.18)

Обозначим 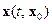– решение системы (14.15) или (14.17). При этом 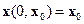, , 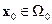а область 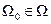такова, что при всех 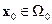и 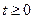решение .

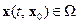Необходимо найти непрерывный вектор k(x) из (14.18), при котором выполняется условие экспоненциального затухания вектора состояния системы, т.е. такой вектор k(x), при котором

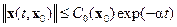. (14.19)

Здесь 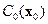и α – положительные постоянные. В этом случае, очевидно, обеспечивается асимптотическая устойчивость положения равновесия x = 0 замкнутой системы (14.15) или, что то же самое, системы (14.17) в некоторой области притяжения .

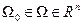Следующая теорема определяет условия существования области притяжения 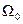положения равновесия x= 0 системы (14.17).

Теорема 14.1. Если в (14.17) матрица D(x) является непрерывной, а коэффициенты её характеристического полинома – постоянными числами, и этот полином удовлетворяет критерию Гурвица, то существует некоторая область 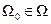такая, что при всех 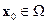и 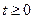выполняется неравенство (14.19), где , . ■

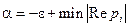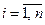Здесь 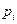– корни характеристического полинома матрицы D(x) (14.18); 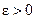– достаточно малое число. Отметим, что если все корни характеристического уравнения матрицы D(x) системы (14.17) имеют строго отрицательные вещественные части, то эта нелинейная система называется гурвицевой.

Справедливость теоремы вытекает из следующих фактов. В силу непрерывности матрицы D(x) и постоянства коэффициентов её гурвицевого характеристического полинома, матрица D(x) стремится при 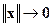к некоторой постоянной матрице 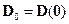, которая является устойчивой. Поэтому существует симметрическая положительно-определённая матрица P такая, что производная по времени функции 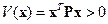на траекториях нелинейной системы (14.17) при достаточно малых 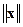является отрицательно-определённой функцией.

Теорема 14.1 не гарантирует асимптотической устойчивости в целом положения равновесия нелинейных гурвицевых систем типа (14.17). Поэтому необходимо всегда оценивать область притяжения их положения равновесия x = 0. Для этой цели целесообразно использовать метод численного моделирования с помощью ЭВМ, так как аналитические методы (например, на основе равенства (12.23)) дают слишком грубые оценки области притяжения. Область начальных условий 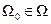, в которой решения системы (14.17) являются затухающими, и является искомой областью притяжения.

Перейдём к выводу расчётных соотношений, позволяющих найти необходимый вектор 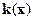из выражения (14.18). Используя свойства определителя, характеристический полином матрицы D(x) (14.18) можно представить следующим образом:

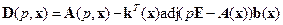
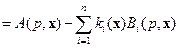, (14.20)

где

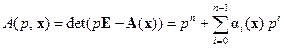, (14.21)

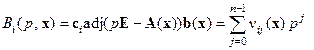. (14.22)

Здесь 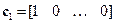, , 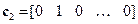, 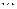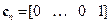– соответствующие строки единичной матрицы Е. Пусть полином

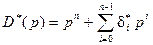(14.23)

является желаемым гурвицевым полиномом матрицы 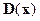системы (14.17). Тогда на основе равенств (14.20) и (14.21) – (14.23) можно составить следующую систему алгебраических

уравнений:

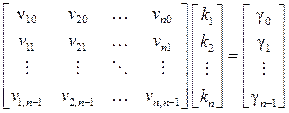, (14.24)

где 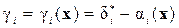, 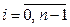. В (14.24) аргументы нелинейных функций из (14.21) и (14.22) опущены для сокращения записи.

Отметим, что определитель матрицы системы (14.24) пропорционален определителю, фигурирующему в условии (14.16). Поэтому если это условие выполняется, то система (14.24) всегда имеет единственное решение. Это решение, зависящее только от вектора x, определяет искомый вектор k(x), при котором решение системы (14.17) удовлетворяет условию (14.18) в некоторой области .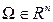

Замечание.Соотношения (14.22) – (14.24) могут использоваться также для определения коэффициентов 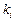модального управления (7.4) и при постоянных матрице A и векторах b, c, т.е. в линейном случае.

Пример 14.2. Найти управление, стабилизирующее частоту синхронного генератора при постоянном напряжении возбуждения и при отсутствии насыщения в магнитных цепях. Синхронный генератор и турбина описываются при этом уравнениями в отклонениях

, ,

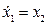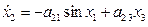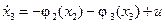, (14.25)

где x₁ – угол поворота ротора относительно синхронной оси вращения, x₂ – скольжение, x₃ – отклонение механической мощности турбины, 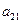, 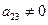– конструктивные постоянные, 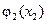, 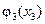– дифференцируемые нелинейности, которые удовлетворяют первому условию (14.14).

Решение. При замене уравнений (14.25) квазилинейной моделью (14.15) её матрица 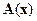и вектор 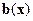примут вид:

, ,

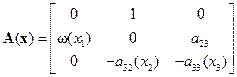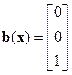где , , .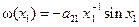

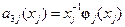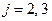Условие (14.16), как нетрудно проверить, в данном случае выполняется, т.е. решение

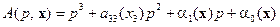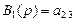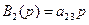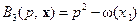задачи синтеза существует. Поэтому по формулам (14.21), (14.22) определяются полиномы: , , и где , .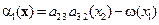

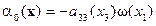Пусть в качестве желаемого выбран полином 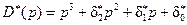, удовлетворяющий критерию Гурвица. Система (14.24) в данном случае имеет решение: 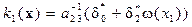, , 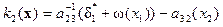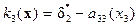. Следовательно, искомое управление для заданной системы (14.25) определяется равенством:

.

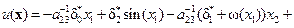
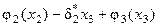Подставляя найденные выражения для матрицы A(x) и функций 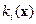, 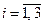в равенство (14.18), найдем матрицу D(x). Далее, определяя по формуле (14.21) её характеристический полином, нетрудно убедиться, что он совпадает с выбранным выше полиномом D*(p), т.е. имеет постоянные коэффициенты и является гурвицевым.

Следовательно, синтезированная система является гурвицевой, и в соответствии с теоремой 14.1 её положение равновесия асимптотически устойчиво в большом. Область притяжения 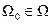положения равновесия синтезированной системы может быть найдена, как отмечалось выше, методом компьютерного моделирования.