Подъёмная сила крыла. Теорема Жуковского
Первая попытка исследовать природу подъёмной силы была сделана итальянским учёным и художником Леонардо да Винчи в 1505 г. Он считал, что подъемная сила, поддерживающая птицу, возникает из-за уплотнения воздуха под крыльями.
В 1852г. Магнус, член-корреспондент Петербургской академии наук, провёл серию опытов для объяснения явления отклонения от вертикальной плоскости вращающихся артиллерийских снарядов. Он показал, что поперечная сила, вызывающая это отклонение, возникает из-за взаимодействия двух потоков воздуха:
· набегающего на снаряд;
· вращающегося вместе со снарядом.
Это явление, получившее название эффект Магнуса, было исследовано в 1902-1906 гг Николаем Егоровичем Жуковским.
В 1906году в своей работе « О присоединённых вихрях» он публикует знаменитую «Теорему Жуковского», объясняющую образование подъемной силы.
Важным понятием, лежащим в основе понимания теоремы Жуковского, является вихрь и определяемая им циркуляция.
Рассмотрим обтекание вращающегося цилиндра (рис. 2.10).
| Рис. 2.10. Эффект Магнуса (вращающийся цилиндр) |
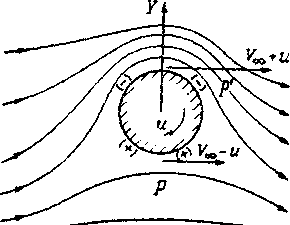 У вращающегося цилиндра спектр обтекания несимметричный, так как на верхней поверхности цилиндра скорость потока и окружная скорость цилиндра складываются, а на нижней поверхности – вычитаются.
У вращающегося цилиндра спектр обтекания несимметричный, так как на верхней поверхности цилиндра скорость потока и окружная скорость цилиндра складываются, а на нижней поверхности – вычитаются.
Из-за неравенства скоростей над и под цилиндром возникает разность давлений, порождающая подъемную силу.
Вследствие вязкости воздух увлекается вращающимся цилиндром и создает вокруг него вихрь.
Вихрем будем называть массу воздуха, вращаюуюся вокруг тела.
Вихрь вовлекает во вращение окружающие его массы воздуха и индуцирует (вызывает) скорости
в окружающей среде. Эти окружные скорости называются индуктивными.
Для определения действующих на цилиндр аэродинамических сил его можно заменить вихрем, дающим то же поле скоростей, что и цилиндр.
Замена вращающегося цилиндра вихрем, который Н.Е.Жуковский назвал присоединенным, и позволила Н.Е. Жуковскому создать вихревую теорию крыла. Согласно этой теории подъемная сила крыла возникает вследствие наложения присоединенного вихря на основной поток.
Интенсивность воздействия вихря на окружающую среду, а значит, и величина подъемной силы, определяется циркуляцией скорости.
| Рис. 2.10. К понятию «циркуляция скорости» |
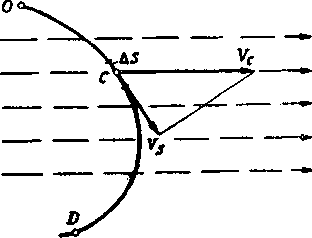 Для понимания сущности циркуляции скорости проведем в установившемся потоке произвольный контур ОD (рис. 2.10). Выделим элемент этого контура, который ввиду его малости можно принять за торезок прямой. Обозначим скорость потока в точке С, находящейся на этом элементе, через Vc, а проекцию этой скорости на элемент контура через Vs. Произведение длины элемента контура на проекцию скорости на контур Vs называется элементарной циркуляцией скорости.
Для понимания сущности циркуляции скорости проведем в установившемся потоке произвольный контур ОD (рис. 2.10). Выделим элемент этого контура, который ввиду его малости можно принять за торезок прямой. Обозначим скорость потока в точке С, находящейся на этом элементе, через Vc, а проекцию этой скорости на элемент контура через Vs. Произведение длины элемента контура на проекцию скорости на контур Vs называется элементарной циркуляцией скорости.
Циркуляция скорости по контуру ОD будет равна сумме элементарных циркуляций.
Г = 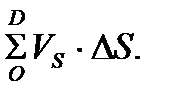
Вычислим циркуляцию скорости по замкнутому контуру в виде окружности радиусом r. Индуктивные скорости в каждой точке окружности, создаваемой вихрем, направлены по касательной к этой окружности и постоянны по величине. Поэтому
Г= 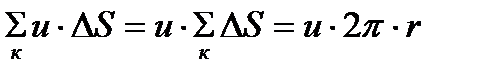
Чем больше циркуляция скорости, тем больше разность скоростей и давлений при наложении циркулярного потока на основной поток, т.е. тем больше подъемная сила.
Циркуляция скорости вокруг цилиндра возникает только при его вращении. Циркуляция вокруг крыла возникает самостоятельно, без помощи вращения.
В расчётной схеме Жуковского крылозаменялось вихрем, вокруг которого образуется циркуляция скорости.
При взаимодействии вихря с плоскопараллельным потоком скорости их суммируются. Над крылом скорость частиц увеличивается, под крылом – уменьшается (рис. 2.11).
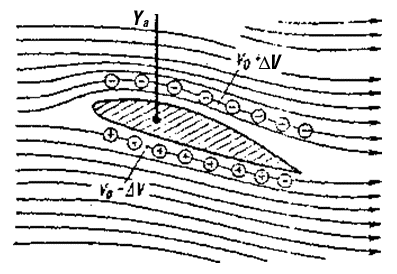
Рис. 2.11. Создание подъемной силы
V 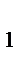 =V
=V 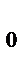 +
+ 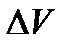 ; V
; V 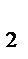 = V
= V 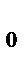 -
- 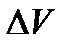 ,
,
где V 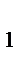 – скорость над профилем крыла, a V
– скорость над профилем крыла, a V 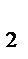 – скорость под профилем крыла.
– скорость под профилем крыла.
Из-за разности скоростей над крылом и под крылом возникает циркуляция скорости.
В соответствии с законом Бернулли разность скоростей приводит к появлению разности давлений над
и под крылом, т.е. к созданию подъемной силы.
Н. Е. Жуковский вывел формулу для определения величины подъемной силы.
Подъёмная сила единицы длины крыла бесконечного размаха равна произведению циркуляции скорости вокруг профиля крыла на плотность и скорость набегающего потока:
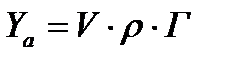
где Г – циркуляция скорости воздуха вокруг профиля крыла;
Yl=1- подъёмная сила для единицы длины крыла.
Теорему Н.Е.Жуковского можно сформулировать так:
Подъемная сила единицы длины крыла бесконечного размаха равна произведению циркуляции скорости вокруг профиля крыла на плотность и скорость набегающего потока.
А для крыла с размахом 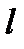 подъемную силу можно определить по формуле:
подъемную силу можно определить по формуле:
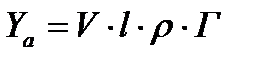 .
.
Из формулы видно, что для увеличения подъемной силы крыла при данной скорости нужно увеличить циркуляцию скорости Г. Это достигается увеличением кривизны профиля, управлением пограничным слоем.
Циркуляция скорости Г пропорциональна хорде профиля крыла b и скорости потока и определяется по формуле:
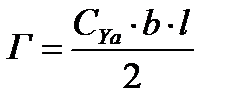
Подставляем Г в формулу Y 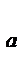 и получаем:
и получаем:
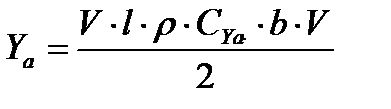 ,
,
но так как lb = S, то
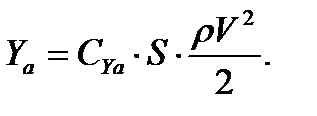
Таким образом, получили знакомую формулу подъемной силы.
Коэффициент подъемной силы СY 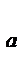 определяет
определяет
зависимость подъемной силы от формы крыла и его положения в потоке.
График зависимости коэффициента подъемной силы CY 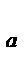 от угла атаки α имеет следующий вид:
от угла атаки α имеет следующий вид:
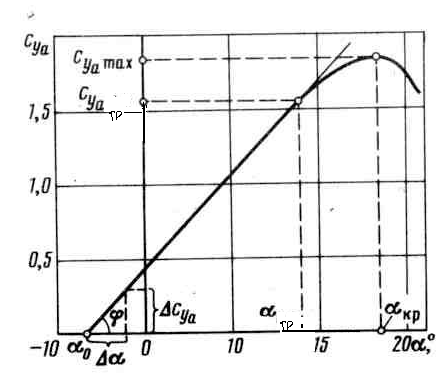
Рис. 2.12. График зависимости Су 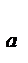 от угла атаки
от угла атаки 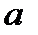
Характерные точки графика:
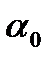 – угол нулевой подъемной силы; это угол атаки, при котором коэффициент подъемной силы СY
– угол нулевой подъемной силы; это угол атаки, при котором коэффициент подъемной силы СY 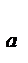 равен нулю.
равен нулю.
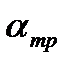 – угол атаки, соответствующий началу срывного обтекания крыла. Он называется углом тряски, т.к. летчик начинает ощущать потряхивание органов управления при выходе на этот угол.
– угол атаки, соответствующий началу срывного обтекания крыла. Он называется углом тряски, т.к. летчик начинает ощущать потряхивание органов управления при выходе на этот угол.
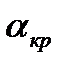 — критический угол атаки, соответствующий максимальному значению коэффициента СY
— критический угол атаки, соответствующий максимальному значению коэффициента СY 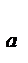 , Он называется критическим, так как при случайном увеличении этого угла происходит отрыв пограничного слоя, самолет становится плохо управляемым, склонным к сваливанию на крыло и переходу в «штопор».
, Он называется критическим, так как при случайном увеличении этого угла происходит отрыв пограничного слоя, самолет становится плохо управляемым, склонным к сваливанию на крыло и переходу в «штопор».
График зависимости CY 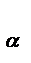 (
( 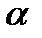 ) можно разделить на три участка:
) можно разделить на три участка:
1) при малых углах атаки пограничный слой плотно прилегает к поверхности крыла и зависимость CY 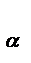 (
( 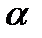 ) носит прямолинейный характер;
) носит прямолинейный характер;
2) 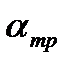 …
… 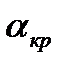 — в этом диапазоне углов атаки в нижних слоях пограничного слоя образуются обратные течения, которые разрыхляют пограничный слой и пытаются оторвать его от поверхности крыла. На этом участке течение графика CY
— в этом диапазоне углов атаки в нижних слоях пограничного слоя образуются обратные течения, которые разрыхляют пограничный слой и пытаются оторвать его от поверхности крыла. На этом участке течение графика CY 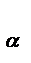 (
( 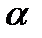 ) становится криволинейным.
) становится криволинейным.
3) α > 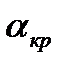 — на этих углах атаки происходит отрыв пограничного слоя от поверхности крыла, подъёмная сила Y
— на этих углах атаки происходит отрыв пограничного слоя от поверхности крыла, подъёмная сила Y 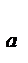 ,следовательно, и коэффициент подъемной силы СY
,следовательно, и коэффициент подъемной силы СY 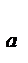 резко падают.
резко падают.
Для симметричного профиля кривая CY 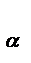
( 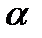 ) проходит через начало координат.
) проходит через начало координат.
Если угол наклона кривой CY 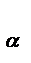 (
( 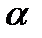 ) относительно оси абсцисс обозначить через
) относительно оси абсцисс обозначить через 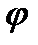 , то
, то
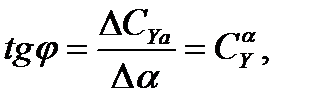
где CY 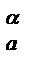 — производная коэффициента подъемной силы по углу атаки
— производная коэффициента подъемной силы по углу атаки 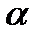 , характеризующая темп изменения коэффициента СYa с изменением угла атаки. Чем больше CY
, характеризующая темп изменения коэффициента СYa с изменением угла атаки. Чем больше CY 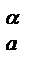 , тем чувствительнее крыло к изменению угла атаки, тем выше несущая способность крыла.
, тем чувствительнее крыло к изменению угла атаки, тем выше несущая способность крыла.
Дата добавления: 2016-12-27; просмотров: 15774;











