Инверторы и преобразователи масштаба

Очень часто возникает необходимость в инвертировании сигнала и изменении масштаба напряжения. Инвертирующий усилитель может обеспечить требуемое изменение масштаба и инверсию знака при выборе соответствующего значения отношения 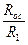(рис. 1.3)

Сигнал переменного тока можно промасштабировать с помощью названных устройств. Но иногда источник сигнала помимо сигнала переменного тока содержит постоянную составляющую, которую для сохранения динамического диапазона звена нецелесообразно усиливать. Поэтому во входную цепь вводят разделительные конденсаторы 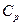(рис. 1.8 а, б).

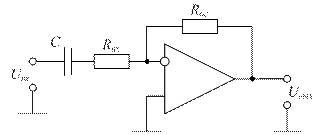
а)

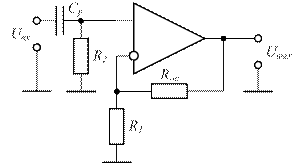
б)

Рисунок 1.8 – Масштабирование сигнала переменного тока

В инвертирующем масштабном звене (рис. 1.8 а) емкость конденсатора С_р рассчитывают, исходя из допустимого уменьшения коэффициента усиления на самой низкой частоте сигнала f_н

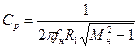(1.12)

где М_н=К_м/К_н – допустимый коэффициент уменьшения коэффициента усиления

К_м – коэффициент усиления на максимальной частоте.

К_н – коэффициент усиления на минимальной частоте.

Расчет сопротивлений R₁ и R_ос звена осуществляют по приведенному ниже соотношению

,

но при низких частотах (десятки – сотни герц) стремятся, увеличить сопротивление R₁ с целью уменьшения емкости С_р.

Неинвертирующее масштабирующее звено (рис. 1.8 б) рассчитывается аналогично расчету инвертирующего звена, при этом

,

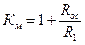а С_р находим по соотношению (1.12), в котором вместо сопротивления R₁ необходимо подставить сопротивление R₂.

Его выбирают достаточно большим (1...2 МW), так как входное сопротивление усилителя здесь практически равно сопротивлению для синфазного сигнала (обычно 100...1000 МW) благодаря контуру обратной связи.

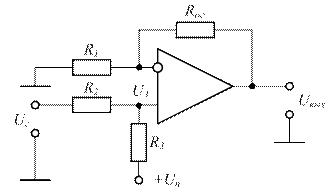
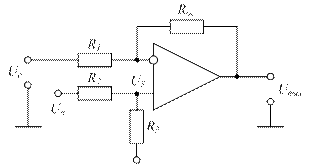
Для устройств, содержащих несколько ОУ и цифровые схемы с одним источником питания, желательно не увеличивать число последних. Тогда на вход ОУ подают напряжение смещения U_см, обеспечивающее на выходе напряжение U_п/2 при U_c=0 (рис. 1.9 а, б)

а)

б)

Рисунок 1.9 – Масштабирующие звенья с одним источником питания

По правилу 1 напряжения на входах одинаковы. Отсюда несложно составить равенства

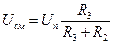– для неинвертирующих входов.

– для инвертирующих входов.

После простейших преобразований находим для инвертирующего звена

, ,

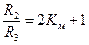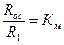а для неинвертирующего звена получим

,

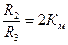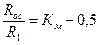
где К_м – заданный коэффициент масштабирования. Значения сопротивлений R₁, ..., R₃, R_ос находят также, как и в обычных масштабных звеньях.

Сумматоры

Инвертирующий усилитель может суммировать несколько входных напряжений. Каждый вход сумматора соединяется с инвертирующим входом ОУ через взвешивающий резистор. Инвертирующий вход называется суммирующим узлом, поскольку здесь суммируются все входные токи и ток обратной связи.

Базовая принципиальная схема суммирующего усилителя представлена на рис. 1.10.

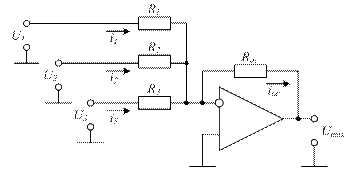
Рисунок 1.10 – Принципиальная схема сумматора

Как и в обычном инвертирующем усилителе, напряжение на инвертирующем входе должно быть равно нулю, следовательно, равен нулю и ток, втекающий в ОУ. Таким образом,

,

, , .

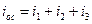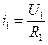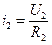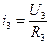Так как на инвертирующем входе действует нулевое напряжение, то .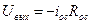

После соответствующих подстановок получаем

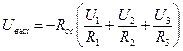
Резистор R_ос определяет общее усиление схемы. Сопротивления R₁, R₂, R₃ задают значения весовых коэффициентов и входных сопротивлений соответствующих каналов.

Рассмотренные выше схемы содержали главным образом резистивные элементы. Инвертирующий усилитель может быть подвергнут дальнейшей модификации путем использования в нем конденсаторов. При этом по-прежнему предполагается, что ОУ имеет идеальные базовые характеристики.

Интеграторы

Интегратор – это электронная схема, которая вырабатывает выходной сигнал, пропорциональный интегралу (по времени) от входного сигнала. На рис. 1.11 показана принципиальная схема простого аналогового интегратора. Один вывод конденсатора присоединен к суммирующему узлу, а другой – к выходу интегратора. Следовательно, напряжение на конденсаторе одновременно является выходным напряжением.

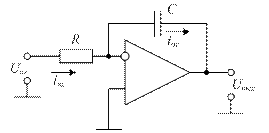
Рисунок 1.11 – Аналоговый интегратор

Выходной сигнал интегратора не удается описать простой алгебраической зависимостью, поскольку при фиксированном входном напряжении выходное напряжение изменяется со скоростью, определяемой параметрами U_вх, R, и C.

Таким образом, для того чтобы найти выходное напряжение, нужно знать длительность действия входного сигнала. Напряжение на первоначально разряженном конденсаторе

,

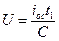где i_ос – ток через конденсатор

t₁ – время интегрирования.

Для положительного U_вх имеем .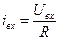

Поскольку i_ос=–i_вх, то с учетом инверсии сигнала получаем

.

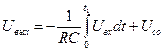Из этого соотношения следует, что U_вых определяется интегралом (с обратным знаком) от входного напряжения в интервале от 0 до t₁, умноженным на масштабный коэффициент 1/RC. Напряжение U_со – это напряжение на конденсаторе в начальный момент времени.

Интегратор на рис. 1.11 имеет недостаток: если напряжение U_вх на входе действует неопределенно долгое время, то выходное напряжение U_вых будет уменьшаться до тех пор, пока не достигнет величины напряжения насыщения ОУ. Это происходит потому, что по постоянному току интегратор работает как усилитель с разомкнутой петлей обратной связи. На рис. 1.12 показана практическая принципиальная схема интегратора, где приняты меры для предотвращения насыщения ОУ. В цикле установки в начальное (исходное) состояние ключ S₁ замкнут, а ключ S₂ разомкнут.

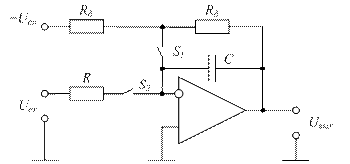
Рисунок 1.12 – Практическая схема интегратора

Схема работает как инвертирующий усилитель, который заряжает конденсатор С до напряжения U_c, равного взятому с обратным знаком опорному напряжению – U_оп. Поскольку входное сопротивление и сопротивление цепи обратной связи одинаковы, то коэффициент усиления инвертирующего усилителя равен –1, U_вых равно U_оп и в начальном состоянии конденсатор заряжен до напряжения U_оп. В цикле интегрирования ключ S₁ разомкнут, а ключ S₂ замкнут. В цикле хранения оба ключа разомкнуты, и выходное напряжение U_вых поддерживается на постоянном уровне для считывания или последующей обработки.

Ключи S₁ и S₂ могут быть контактами реле, твердотельными ключами (например, на полевых транзисторах) или аналоговыми ключами. Работой ключей управляют внешние логические устройства.

Это упрощает установку начальных условий и запуск интегрирования в тех случаях, когда для решения дифференциального уравнения используется несколько интеграторов. На рис. 1.13 иллюстрируется последовательность рабочих циклов интегратора.

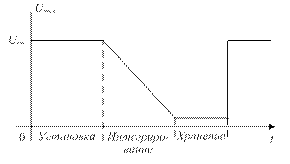
Рисунок 1.13 – Рабочие циклы интегратора

Дифференциаторы

Дифференциатор вырабатывает выходной сигнал, пропорциональный скорости изменения во времени входного сигнала. На рис. 1.14 показана принципиальная схема простого дифференциатора.

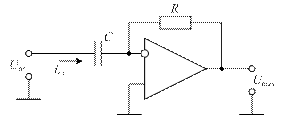
Рисунок 1.14 – Принципиальная схема дифференциатора

Ток через конденсатор 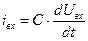. Если производная 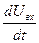положительна, ток течет в таком направлении, что формируется отрицательное выходное напряжение. Таким образом, .

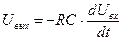Этот метод дифференцирования сигнала кажется простым, но при его практической реализации возникают проблемы. Главной проблемой при расчете дифференциаторов является то, что коэффициент усиления увеличивается при возрастании частоты. Таким образом, дифференциаторы очень восприимчивы к высокочастотным помехам. Классическое решение проблемы заключается во включении последовательно с входным конденсатором низкоомного резистора (с сопротивлением порядка 50 W), что приводит к снижению коэффициента усиления на высоких частотах.

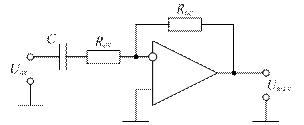
Рисунок 1.15 – Практическая схема дифференциатора

Добавление такого резистора дает схему дифференциатора, в большей степени приближенную к действительной, потому что последовательно с емкостью входного конденсатора всегда оказывается включенным некоторое сопротивление источника сигнала.

С другой стороны, в ряде случаев применение дифференциатора дает преимущества, позволяя обнаружить присутствие искажений или высокочастотных помех в сигнале. С помощью дифференциатора можно нередко обнаружить скрытую информацию, которая не обнаруживается в исходном сигнале.

Отметим также, что в ряде случаев при необходимости построения устойчивого дифференциатора (например, в ПИД-регуляторе) используют схему с интегратором в обратной связи.

На рис. 1.16 приведена функциональная схема дифференциатора.

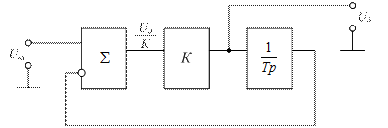
Рисунок 1.16 – Функциональная схема дифференциатора с интегратором в обратной связи

В приведенной схеме интегратор представлен передаточной функцией (подробнее см. курс «Теория автоматического управления»), что облегчает получение уравнения связывающего входной сигнал U 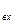с выходным U_д.

Для выходного сигнала сумматора в операторной форме можно записать

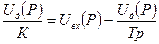
и далее

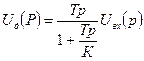
И окончательно в операторной форме

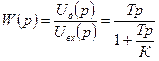
Полученное выражение представляет собой передаточную функцию реального дифференцирующего звена (подробнее см. курс ТАУ).