ЛОГИЧЕСКИЙ СИНТЕЗ ПЕРЕКЛЮЧАТЕЛЬНЫХ И ВЫЧИСЛИТЕЛЬНЫХ СХЕМ

В вычислительных и других автоматических устройствах широко применяются электрические схемы, содержащие множество переключательных элементов: реле, выключателей и т. п. При разработке таких схем с успехом может быть использован аппарат алгебры логики.

Переключательная схема — схематическое изображение некоторого устройства, состоящего из переключателей и соединяющих их проводников, а также входов и выходов, на которые подается и с которых снимается электрический сигнал.

Каждый переключатель имеет только два состояния: замкнутое и разомкнутое. Переключателю X поставим в соответствие логическую переменную х, которая принимает значение 1 только в том случае, когда переключатель X замкнут и схема проводит ток; если же переключатель разомкнут, то переменная х равна нолю. При этом два переключателя X и Х связаны таким образом, что когда X замкнут, то X разомкнут, и наоборот. Следовательно, если переключателю X поставлена в соответствие логическая переменная х, то переключателю X должна соответствовать переменная х.

Всей переключательной схеме также можно поставить в соответствие логическую переменную, равную единице, если схема проводит ток, и равную нолю — если не проводит. Эта переменная является функцией от переменных, соответствующих всем переключателям схемы, и называется функцией проводимости.

Рассмотрим функции проводимости F некоторых переключательных схем:

Схема не содержит переключателей и проводит ток всегда, следовательно, F—1;

Схема содержит один постоянно разомкнутый контакт, следовательно, F— 0;

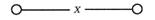
Схема проводит ток, когда переключатель х замкнут, и не проводит, когда х разомкнут, следовательно, F(x) =x;

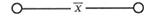
Схема проводит ток, когда переключатель х разомкнут, и не проводит, когда х замкнут, следовательно,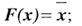

Схема проводит ток, когда оба переключателя замкнуты, следовательно, F(x) = х · у;

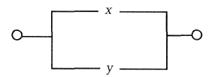
Схема проводит ток, когда хотя бы один из переключателей замкнут, следовательно, F(x) =x v y.

При рассмотрении переключательных схем решают, как правило, одну из основных задач: синтез или анализ схемы.

Синтез переключательной схемы по заданным условиям ее работы сводится к следующим трем этапам:

· составление функции проводимости по заданным условиям;

· упрощение этой функции;

· построение соответствующей схемы.

Анализ схемы характеризуется следующими этапами:

определение значений функции проводимости при всех возможных наборах входящих в эту функцию переменных;

получение упрощенной формулы.

Рассмотрим примеры решения задач синтеза и анализа несложных переключательных схем.

Задачи синтеза.

Построим схему, содержащую 4 переключателя х, у, z и t, такую, чтобы она проводила ток тогда и только тогда, когда замкнут контакт переключателя t и какой-нибудь из остальных трех контактов.

Решение. Функция проводимости для данного случая имеет вид F(x,у,z,t) = t(x v y v z), a схема имеет вид:

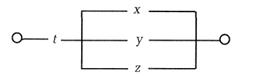
Задачи анализа.

1) Найдем функцию проводимости схемы:

а)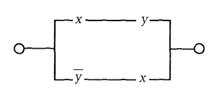

Решение:

Функция проводимости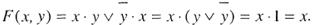

Упрощенная схема: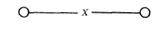

б)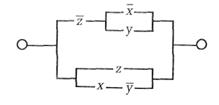

Решение:

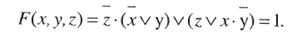
Здесь первое логическое слагаемое 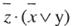является отрицанием второго логического слагаемого 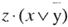, а дизъюнкция переменной с ее инверсией равна 1.

Упрощенная схема: