Функциональное и логическое программирование

Как известно, теоретические основы императивного программирования были заложены ещё в 1930-х годах Аланом Тьюрингом и Джоном фон Нейманом. Теория, положенная в основу функционального подхода, также родилась в 20-х — 30-х годах. В числе разработчиков математических основ функционального программирования можно назвать Мозеса Шёнфинкеля и Хаскелла Карри, разработавших комбинаторную логику, и Алонзо Чёрча, создателя λ-исчисления.

Теория так и оставалась теорией, пока в начале 1950-х годов Джон Маккарти не разработал язык Лисп, который стал первым почти функциональным языком программирования и многие годы оставался единственным таковым. Лисп всё ещё используется (также как и Фортран), после многих лет эволюции он удовлетворяет современным запросам, которые заставляют разработчиков программ взваливать как можно бо́льшую но́шу на компилятор, облегчив так свой труд. Нужда в этом возникла из-за всё более возрастающей сложности программного обеспечения.

В связи с этим обстоятельством всё бо́льшую роль начинает играть типизация. В конце 70-х — начале 80-х годов XX века интенсивно разрабатываются модели типизации, подходящие для функциональных языков. Большинство этих моделей включали в себя поддержку таких мощных механизмов как абстракция данных и полиморфизм. Появляется множество типизированных функциональных языков: ML, Scheme, Hope, Miranda, Clean и многие другие. Вдобавок постоянно увеличивается число диалектов.

В результате вышло так, что практически каждая группа, занимающаяся функциональным программированием, использовала собственный язык. Это препятствовало дальнейшему распространению этих языков и порождало многие более мелкие проблемы. Чтобы исправить положение, объединённая группа ведущих исследователей в области функционального программирования решила воссоздать достоинства различных языков в новом универсальном функциональном языке. Первая реализация этого языка, названного Haskell в честь Хаскелла Карри, была создана в начале 90-х годов. Ныне действителен стандарт Haskell-98.

Большинство функциональных языков программирования реализуются как интерпретируемые, следуя традициям Лиспа (примечание: большая часть современных реализаций Лиспа содержат компиляторы в машинный код). Таковые удобны для быстрой отладки программ, исключая длительную фазу компиляции, укорачивая обычный цикл разработки. С другой стороны, интерпретаторы в сравнении с компиляторами обычно проигрывают по скорости выполнения. Поэтому помимо интерпретаторов существуют и компиляторы, генерирующие неплохой машинный код (например, Objective Caml) или код на Си/Си++ (например, Glasgow Haskell Compiler). Что показательно, практически каждый компилятор с функционального языка реализован на этом же са́мом языке. Это же характерно и для современных реализаций Лиспа, кроме того среда разработки Лиспа позволяет выполнять компиляцию отдельных частей программы без остановки программы (вплоть до добавления методов и изменения определений классов).

В этом курсе для описания примеров функционального программирования будет использован либо некий абстрактный функциональный язык, приближенный к математической нотации, либо Haskell, бесплатные компиляторы которого можно скачать с сайта haskell.org.

Свойства функциональных языков

Как основные свойства функциональных языков кратко рассмотрим следующие:

- краткость и простота;

- строгая типизация;

- модульность;

- функции — это значения;

- чистота (отсутствие побочных эффектов);

- отложенные (ленивые) вычисления.

Краткость и простота

Программы на функциональных языках обычно короче и проще, чем те же самые программы на императивных языках. Сравним программы на Си и на абстрактном функциональном языке на примере сортировки списка быстрым методом Хоара (пример, уже ста́вший классическим при описании преимуществ функциональных языков).

Пример 1. Быстрая сортировка Хоара на Си

Строгая типизация

Из современных языков программирования многие суть строго типизированные. Строгая типизация позволяет компилятору оптимизировать программы, использовать конкретные типы и контейнеры конкретных типов вместо шаблонных, вариантных типов, более громоздких в реализации. Кроме того, строгая типизация позволяет оградиться от части ошибок, связанных с неожидаемым «видом» входных (и выходных) данных, причем это происходит на стадии компиляции, не отнимая на такие проверки время при работе программы. Система типов также способствует «документированию» программы: любая подпрограмма является функцией в математическом смысле слова, отображая одно множество (входное) на другое (выходное), и типы определяют эти множества. Читабельность программ повышается, если используются псевдонимы типов или сложные типы, собранные на основе простых, вместо базовых элементарных целых, строк и т. п.

В примере с быстрой сортировкой Хоара видно, что есть ещё одно важное отличие между вариантом на Си и вариантом на Хаскеле: функция на Си сортирует список значений типа int (целых чисел), а функция на абстрактном функциональном языке — список значений любого типа, принадлежащего к классу упорядоченных величин. Последняя функция может сортировать и список целых чисел, и список чисел с плавающей точкой, и список строк. Можно описать какой-нибудь новый тип. Определив для этого типа операции сравнения, возможно без перекомпиляции использовать функцию quickSort и со списками значений этого нового типа. Это полезное свойство системы типов называется параметрическим или истинным полиморфизмом, и поддерживается большинством функциональных языков.

Ещё одно проявление полиморфизма — перегрузка функций, позволяющая давать разным, но подобным функциям одинаковые имена. Типичный пример перегруженной операции — обычная операция сложения. Функции сложения для целых чисел и чисел с плавающей точкой различны, но для удобства они носят одно имя. Некоторые функциональные языки помимо параметрического полиморфизма поддерживают и перегрузку операций.

В языке Си++ имеется такое понятие, как шаблон, которое позволяет программисту определять полиморфные функции, подобные quickSort. В стандартную библиотеку Си++ — STL — входит такая функция и множество других полиморфных функций. Но шаблоны Си++, как и родовые функции Ады, на самом деле порождают множество перегруженных функций, которые, кстати, нужно каждый раз компилировать, что неблагоприятно сказывается на времени компиляции и размере кода. А в функциональных языках полиморфная функция quickSort — это одна единственная функция.

В некоторых языках, например в Аде, строгая типизация вынуждает программиста явно описывать тип всех значений и функций. Для избежания этого, в строго типизированные функциональные языки встроен механизм, позволяющий компилятору определять типы констант, выражений и функций из контекста, — механизм вывода типов. Известно несколько таких механизмов, однако большинство из них суть разновидности модели типизации Хиндли — Милнера, разработанной в начале 1980-х. Поэтому в большинстве случаев можно не указывать типы функций.

Модульность

Механизм модульности позволяет разделять программы на несколько сравнительно независимых частей (модулей) с чётко определёнными связями между ними. Так облегчается процесс проектирования и последующей поддержки больши́х программных систем. Поддержка модульности не есть свойство именно функциональных языков программирования, но поддерживается большинством таких языков. Существуют очень развитые модульные императивные языки. Примеры: Modula-2 и Ada-95.

Функции суть значения

В функциональных языках, равно как и вообще в языках программирования и математике, функции могут быть переданы другим функциям в качестве аргумента или возвращены в качестве результата. Функции, принимающие функциональные аргументы, называются функциями высших порядков или функционалами. Самый, пожалуй, известный функционал — функция map. Она применяет некоторую функцию ко всем элементам списка, формируя из результатов заданной функции другой список. Например, определив функцию возведения целого числа в квадрат как:

Можно воспользоваться функцией map для возведения в квадрат всех элементов некоторого списка:

Результатом будет список [1, 4, 9, 16].

Чистота (отсутствие побочных эффектов)

В императивных языках функция в процессе своего выполнения может читать и изменять значения глобальных переменных и осуществлять операции ввода-вывода. Поэтому, если вызвать одну и ту же функцию дважды с одним и тем же аргументом, может случиться так, что в качестве результата вычислятся два различных значения. Такая функция называется функцией с побочными эффектами.

Описывать функции без побочных эффектов позволяет практически любой язык. Однако некоторые языки поощряют или даже требуют от функции побочных эффектов. Например, во многих объектно-ориентированных языках в функцию-член класса передаётся скрытый параметр (чаще он называется this или self), который эта функция неявно изменяет.

В чистом функциональном программировании оператор присваивания отсутствует, объекты нельзя изменять и уничтожать, можно только создавать новые путём разбора и сбора существующих. О ненужных объектах позаботится встроенный в язык сборщик мусора. Благодаря этому в чистых функциональных языках все функции свободны от побочных эффектов. Однако это не мешает этим языкам имитировать некоторые полезные императивные свойства, такие как исключения и изменяемые массивы.

Каковы же преимущества чистых функциональных языков? Помимо упрощения анализа программ есть ещё одно — параллелизм. Раз все функции для вычислений используют только свои параметры, мы можем вычислять независимые функции в произвольном порядке или параллельно, на результат вычислений это не повлияет. Причём параллелизм этот может быть организован не только на уровне компилятора языка, но и на уровне архитектуры. В нескольких научных лабораториях уже разработаны и используются экспериментальные компьютеры, основанные на подобных архитектурах. В качестве примера можно привести Lisp-машину.

Отложенные вычисления

В традиционных языках программирования (например, Си++) вызов функции приводит к вычислению всех аргументов. Этот метод вызова функции называется вызов по значению. Если какой-либо аргумент не использовался в функции, то результат вычислений пропадает, следовательно, вычисления были произведены впустую. В каком-то смысле противоположностью вызова по значению является вызов по необходимости. В этом случае аргумент вычисляется, только если он нужен для вычисления результата. Примером такого поведения можно взять оператор конъюнкции всё из того же Си++ (&&), который не вычисляет значение второго аргумента, если первый аргумент имеет ложное значение.

Если функциональный язык не поддерживает отложенные вычисления, то он называется строгим. На самом деле, в таких языках порядок вычисления строго определён. В качестве примера строгих языков можно привести Scheme, Standard ML и Caml. Языки, использующие отложенные вычисления, называются нестрогими. Haskell — нестрогий язык, так же как, например, Gofer и Miranda. Нестрогие языки зачастую являются чистыми.

Очень часто строгие языки включают в себя средства поддержки некоторых полезных возможностей, присущих нестрогим языкам, например бесконечных списков. В поставке Standard ML присутствует специальный модуль для поддержки отложенных вычислений. А Objective Caml помимо этого поддерживает дополнительное специальное слово lazy и конструкцию для списков значений, вычисляемых по необходимости.

Решаемые задачи

В качестве задач, традиционно рассматриваемых в курсах функционального программирования, можно выделить следующие:

1. Получение остаточной процедуры.

Если даны следующие объекты:

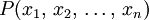- — некоторая процедура.

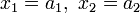- — известные значения параметров.

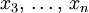- — неизвестные значения параметров.

Требуется получить остаточную процедуру 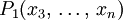. Эта задача решается только на узком классе программ.

2. Построение математического описания функций.

Пусть имеется программа P. Для неё определены входные значения и выходные значения 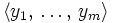. Требуется построить математическое описание функции

.

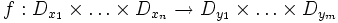3. Определение формальной семантики языка программирования.

4. Описание динамических структур данных.

5. Автоматическое построение «значительной» части программы по описанию структур данных, которые обрабатываются создаваемой программой.

6. Доказательство наличия некоторого свойства программы.

7. Эквивалентная трансформация программ.

Все эти задачи достаточно легко решаются средствами функционального программирования, но практически неразрешимы в императивных языках.

Логи́ческое программи́рование — парадигма программирования, основанная на автоматическом доказательстве теорем, а также раздел дискретной математики, изучающий принципы логического вывода информации на основе заданных фактов и правил вывода. Логическое программирование основано на теории и аппарате математической логики с использованием математических принципов резолюций.

Самым известным языком логического программирования является Prolog.

Первым языком логического программирования был язык Planner, в котором была заложена возможность автоматического вывода результата из данных и заданных правил перебора вариантов (совокупность которых называлась планом). Planner использовался для того, чтобы понизить требования к вычислительным ресурсам (с помощью метода backtracking) и обеспечить возможность вывода фактов, без активного использования стека. Затем был разработан язык Prolog, который не требовал плана перебора вариантов и был, в этом смысле, упрощением языка Planner.

От языка Planner также произошли логические языки программирования QA-4, Popler, Conniver и QLISP. Языки программирования Mercury, Visual Prolog, Oz и Fril произошли уже от языка Prolog. На базе языка Planner было разработано также несколько альтернативных языков логического программирования, не основанных на методе backtracking, например, Ether

Еще в конце 1970-х годов стала отчетливо просматриваться тенденция к использованию в исследованиях в области искусственного интеллекта "формальных" методов, т.е. основанных на аппарате математической логики. Эти методы противопоставлялись более интуитивным и менее формализованным эвристическим методам, скажем, таким, которые были использованы в системе MYCIN. Для того чтобы стало ясно, что все это значит, нужно познакомить вас с логическими языками, а затем показать, как соотносятся их свойства с теми методами рассуждений, которые должны поддерживать типовые экспертные системы.

Математическая логика является формальным языком в том смысле, что в отношении любой последовательности символов она позволяет сказать, удовлетворяет ли эта последовательность правилам конструирования выражений в этом языке (формулам). Обычно формальным языкам противопоставляются естественные, такие как французский и английский, в которых грамматические правила не являются жесткими. Утверждение, что логика является исчислением с определенными синтаксическими правилами логического вывода, означает, что влияние одних членов выражения на другие зависит только от формы выражения в данном языке и ни коим образом не зависит от каких-либо посторонних идей или интуитивных предположений.

Под автоматическим формированием суждений (automated reasoning) понимается поведение некоторой компьютерной программы, которая строит логический вывод на основании определенных законов. Так, нельзя отнести к классу программ автоматического формирования суждений программу, которая моделирует подбрасывание монетки, чтобы определить, следует ли одна формула из набора других. (В литературе также часто встречается термин автоматическая дедукция (automated deduction), равнозначный по смыслу термину автоматическое формирование суждений.)

При реализации автоматического формирования суждений, как правило, стремятся к максимально возможному единообразию и стандартизации в представлении формул, но в то же время в литературе часто приходится сталкиваться с самыми разнообразными системами обозначений, относящихся к логике. Основными синтаксическими схемами представления выражений являются конъюнктивная нормальная форма (conjunctive normal form— CNF), полная фразовая форма (full clausal form) и фраза Хорна (Horn clause), последняя является подмножеством полной фразовой формы. Далее мы увидим, что эти формы представления значительно упрощают процедуру логического вывода, но сначала рассмотрим некоторые вопросы исчисления высказываний и предикатов.

Фразы Хорна (Horn clause) представляют собой подмножество фраз, содержащих только один позитивный литерал. В общем виде фраза Хорна представляется выражением

В языке PROLOG эта же фраза записывается в таком виде (обратите внимание на символ точки в конце):

р :- q1,...,qn. Такая фраза интерпретируется следующим образом:

"Для всех значений переменных в фразе p истинно, если истинны q1 и ... и qn",

т.е. пара символов ":-" читается как "если", а запятые читаются как "и".

PROLOG — это не совсем обычный язык программирования, в котором программа состоит в основном из логических формул, а процесс выполнения программы представляет собой доказательство теоремы определенного вида.

Фраза в форме

р :- q1, ...,qn.

может рассматриваться в качестве процедуры. Такая процедура предполагает следующий порядок выполнения операций.

(1) Литерал цели сопоставляется с литералом р (унифицируется с р), который называется головой фразы.

(2)Хвост фразы ql, ...,qn конкретизируется подстановкой значений переменных (или унификаторов), сформированных в результате этого сопоставления.

(3) Конкретизированные термы хвостовой части образуют затем множество подцелей, которые могут быть использованы другими процедурами.

Таким образом, сопоставление (или унификация) играет ту же роль, что и передача параметров функции в других, более привычных языках программирования.

Правила логического вывода, теория ориентированных графов и математическая логика были изобретены задолго до появления такой области исследований, как искусственный интеллект. Но именно исследования в этой области позволили адаптировать формальный аппарат этих теорий к задачам представления знаний и отыскать высокоэффективные средства их реализации. Развитие современных продукционных, объектно-ориентированных систем и систем процедурной дедукции в значительной мере определяется такими приложениями искусственного интеллекта, как проблемы классификации и конструирования, описанные в ряде глав данной книги.

Хотя в ходе исследований искусственного интеллекта появилось множество самых различных языков представления, все они обладают рядом сходных свойств.

Во-первых, все такие языки являются декларативными в том смысле, что позволяют описывать знания, имеющие отношение к решению конкретной задачи, а не способ ее решения. В большинстве экспертных систем используется архитектура, в которой знания отделены от машины логического вывода. Это позволяет проводить эксперименты с использованием одних и тех же знаний в разных режимах обработки. Некоторые новые архитектурные решения, например использующие доску объявлений, позволяют представлять управляющие знания декларативно и обрабатывать их так же, как и другие виды знаний.

Во-вторых, все такие языки организованы по модульному принципу. Подобно тому, как сам язык скрывает от пользователя детали механизма реализации, отдельные модули знаний скрывают детали своей реализации друг от друга, общаясь через глобальную структуру данных (в продукционных системах и системах на основе доски объявлений) или посредством определенных протоколов (в объектно-ориентированных системах). Это позволяет наращивать объем базы знаний и использовать методику отработки проектируемой системы на прототипах.

В-третьих, механизм вызова процедур в таких языках основан на сопоставлении образцов в той или иной форме. Активизация правил в продукционных системах, включение источников знаний в системах с доской объявлений и резолюция фраз в дедуктивных системах в той или иной форме используют такое сопоставление. Это очень мощный и достаточно общий механизм, который способствует модульной организации компонентов системы, хотя и требует определенных вычислительных ресурсов.

Языки представления знаний обычно реализуются в виде системы логического вывода, управляемой сопоставлением образцов. Программа на любом из языков такого рода состоит из множества относительно независимых модулей (правил, структур или фраз), которые сопоставляются со входными данными и манипулируют имеющимися в памяти данными. В любой такой системе имеются три существенных компонента.

Набор модулей, каждый из которых может быть активизирован данными, поступающими на вход системы, если эти данные соответствуют образцу, определенному для этого модуля.

Одна или несколько динамических структур данных, которые могут анализироваться и модифицироваться активизированным модулем.

Интерпретатор, который циклически управляет выбором и активизацией модулей.

Исследования в этой области в последние годы концентрируются вокруг следующих задач:

- поиск эффективных методов реализации интерпретаторов;

- создание на основе "чистых формализмов" программных средств, пригодных для практического применения;

- проведение экспериментов со "смешанными" формализмами, объединяющими разные парадигмы.

На сегодняшний день такие языки, как CLIPS, предоставляют в распоряжение пользователя множество разнообразных средств представления знаний и манипулирования ими, которые в руках специалистов позволяют создавать программы для решения широкого круга практических проблем.