Лекция 2 — Нагрев и плавление электрода при дуговой сварке. Нагрев и плавление электродной проволоки при автоматической сварке.
Нагрев и плавление электрода при дуговой сварке
Нагрев электрода в процессе сварки обусловлен действием двух источников тепла:
1) Теплом электрической дуги, действующим на прилегающий к торцу участок длиной не более 5–10 мм.
2) Теплом, возникающим в объеме электродного стержня в результате сопротивления электрода протекающему току.
Поскольку нагрев электрода дугой распространяется только на небольшую длину, то при рассмотрении процесса нагрева всего электрода влияние дуги можно не учитывать.
Определим отдельно нагрев электрода от протекающего тока. Уравнение теплового баланса нагрева стержня проходящим током составим для единицы длины стержня
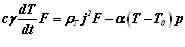 (2.36)
(2.36)
Первый член уравнения представляет собой накопление теплоты в стержне сечением F в единицу времени; второй член выражает количество теплоты, выделяемой током плотностью j в стержне с удельным сопротивлением ρТ; третий член представляет собой количество теплоты, отдаваемое с поверхности стержня периметром р. Решение представленного дифференциального уравнения, если принять коэффициенты сγ, ρТ, и α не зависящими от температуры, может оказаться неточным при изменении температуры в широких пределах.
Удельное сопротивление металлов возрастает с температурой. Зависимость величины 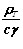 от температуры для ряда материалов можно приближенно описать линейным соотношением
от температуры для ряда материалов можно приближенно описать линейным соотношением
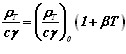 , (2.37)
, (2.37)
где 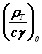 – значение коэффициента при Т = 0 ºС.
– значение коэффициента при Т = 0 ºС.
Для тонких стержней, какими являются сварочные электроды, роль теплоотдачи довольно велика. Коэффициент 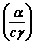 следует принимать не постоянным, как это обычно делается в расчетах, а зависящим от температуры
следует принимать не постоянным, как это обычно делается в расчетах, а зависящим от температуры
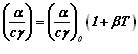 . (2.38)
. (2.38)
Подставляя уравнения (2.37) и (2.38) в дифференциальное уравнение (2.36), находим его решение
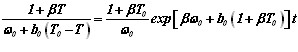 (2.39)
(2.39)
где 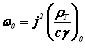 – начальная скорость нагрева;
– начальная скорость нагрева;
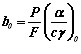 – начальный коэффициент температуроотдачи для стержня.
– начальный коэффициент температуроотдачи для стержня.
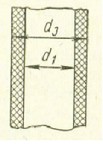
Рис. 2.36
Точность определения температуры по уравнению (2.39) зависит от выбора постоянных коэффициентов, определяемых опытным путем. Для электродов с покрытием величина сγ в уравнении (2.39) выражает среднюю теплоемкость стержня и покрытия, периметр Р = πd3, поперечное сечение F = πd12/4 (Рис. 2.36)
Вычисления по формуле (2.39) упрощаются при использовании номограммы Рис. 2.37. На номограмме принято условное обозначение
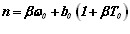
Численные значения коэффициентов при расчете температуры подогрева электродов рекомендуется выбирать по таблице 2.2.
Таблица 2.2 – Значения коэффициентов при расчете нагрева стержней
| Тип электрода | Род тока | β, 1/градус | ω0, градус/сек | b0, 1/градус | |
| Проволока | Покрытие | ||||
| Малоугле- родистая сталь | Меловое ОММ-5 и УОНИ-13 | Постоян. Перемен. Постоян. Перемен. | 4,17·10–3 3,33·10–3 5,00·10–3 4,17·10–3 | 3,1·10–3j2 3,7·10–2j2 2,4·10–2j2 2,7·10–2j2 | 1,17·10–2/d1 1,40·10–2/d1 0,96·10–2/d1 0,08·10–2/d1 |
Здесь 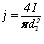 брать в А/мм2 и d1 – брать в мм.
брать в А/мм2 и d1 – брать в мм.
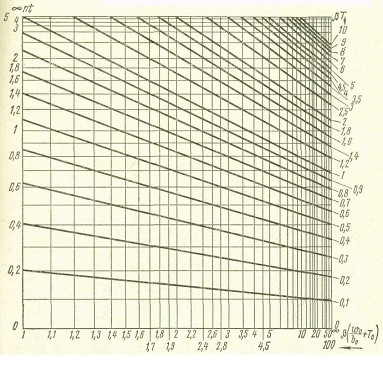
Рис. 2.37 – Номограмма для расчета нагрева стальных электродов током
Для определения температуры нагрева стержня при протекании по нему тока в течение времени t, необходимо определить величину nt, затем величину 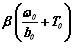 . Далее найти точку их пересечения в прямоугольной системе координат. Из точки пересечения провести прямую, параллельную ближайшей наклонной прямой на номограмме. Ответ прочитаем по правой вертикальной оси в виде произведения βТ. Поделив полученный результат на β найдем искомую величину.
. Далее найти точку их пересечения в прямоугольной системе координат. Из точки пересечения провести прямую, параллельную ближайшей наклонной прямой на номограмме. Ответ прочитаем по правой вертикальной оси в виде произведения βТ. Поделив полученный результат на β найдем искомую величину.
Вычисления и экспериментальные данные показывают, что скорость нагрева электрода существенно зависит от удельного сопротивления материала стержня. Стержни из аустенитной стали при температурах до 600 0С имеют значительно большее значение ρТ, чем стержни из малоуглеродистой стали. Поэтому аустенитные стержни нагреваются значительно быстрее, чем малоуглеродистые. Подобным же образом влияет и плотность тока. Чем выше плотность тока, тем выше температура нагрева. Тонкие электроды вследствие повышенной теплоотдачи нагреваются медленнее, чем толстые, если плотности тока одинаковы.
Помимо нагрева проходящим током, электрод нагревается вторым источником тепла – дугой. Расчетную схему процесса нагрева электрода дугой можно представить следующим образом: тело – полубесконечный стержень, источник тепла – плоский, постоянно действующий, подвижный. Используя уравнение предельного состояния процесса распространения теплоты от подвижного плоского источника в стержне в области впереди источника, то есть х>0 при “b” = 0, получаем распределение температур в стержне в виде уравнения
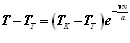 (2.40)
(2.40)
где х – расстояние от торца электрода до исследуемой точки, [см];
TT – температура подогрева электродного стержня током;
TK – температура нагреваемого дугой торца электрода. Условно считаем ТК равной средней температуре капель металла (для стали ТК = 2300–2500 0С)
График распределения температур по длине электрода в различное время после начала горения дуги будет иметь вид

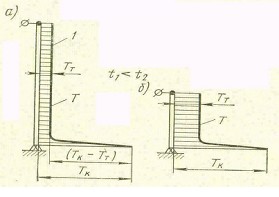
Рис. 2.38 – График распределения температур по длине электрода
в различные моменты времени после начала горения дуги.
При автоматической дуговой сварке проволока нагревается также двумя источниками теплоты – проходящим током и дугой. Особенностью автоматической сварки по сравнению с ручной является то, что при автоматической сварке ток подводится с помощью скользящего контакта на небольшом расстоянии от дуги, то есть ток не проходит по всей длине стержня, как при ручной сварке электродами. В результате этого уменьшается вредное влияние предварительного подогрева стержня, что в свою очередь, дает возможность значительно повысить плотность тока. При этом производительность расплавления электродной проволоки возрастает в несколько раз.
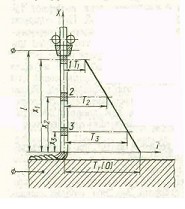 Рис. 2.39 – К расчету нагрева электродной проволоки протекающим по ней током при автоматической сварке.
Рис. 2.39 – К расчету нагрева электродной проволоки протекающим по ней током при автоматической сварке.
| 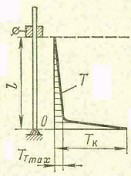 Рис. 2.40 – Суммарный график распределения температур по вылету электрода при автоматической сварке.
Рис. 2.40 – Суммарный график распределения температур по вылету электрода при автоматической сварке.
|
Каждый элемент проволоки, подающийся в дугу со скоростью w см/сек, нагревается током на пути от токоподвода до дуги. Если в некоторый произвольный момент времени рассмотреть тепловое состояние бесконечно малых участков электродной проволоки 1, 2, 3, расположенных на расстояниях х1, х2, х3 от начала координат, совмещенного с дугой, то станет очевидным, что элемент 1 нагревался в течение времени 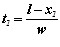 , элемент 2 – в течение времени
, элемент 2 – в течение времени 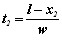 и так далее. Максимальное время нагрева
и так далее. Максимальное время нагрева 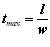 . Определение
. Определение  может быть осуществлено по номограмме. Тогда распределение температур по длине вылета электрода представится прямой линией (грубо), соединяющей
может быть осуществлено по номограмме. Тогда распределение температур по длине вылета электрода представится прямой линией (грубо), соединяющей 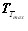 и 0 0С (Рис. 2.39).
и 0 0С (Рис. 2.39).
Суммарный же график распределения температур по длине электрода с учетом действия двух источников тепла представлен на Рис. 2.40.
Контрольные вопросы:
1. Каковы особенности нагрева вылета электродной проволоки теплом Джоуля-Ленца и влияния этого нагрева на производительность сварки?
2. Как рассчитывается нагрев электрода и электродного вылета теплом Джоуля-Ленца?
3. Как рассчитывается нагрев электрода и электродного вылета теплом дуги?
4. Какие факторы влияют на распределение температур вдоль оси электрода?
5. Пути повышения производительности процесса наплавки и проплавления.
Дата добавления: 2016-12-09; просмотров: 4597;











