Истечение жидкости через отверстия

Рассмотрим случай истечения жидкости при постоянном напоре (рис. 24). Для получения расчетной зависимости запишем уравнение Бернулли для двух сечений 1 – 1 и 2 – 2 относительно плоскости сравнения О-О. Примем к сведе-

нию, что жидкость вытекает в воздушное пространство с атмосферным давлением, а на поверхности жидкости также давление атмосферное, и имеет место только местное сопротивление. Тогда 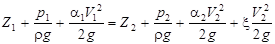, (103)

Рис. 24. Истечение жидкости через

малое отверстие при посто-

янном напоре

где ξ – коэффициент местного сопротивления отверстия.

Для первого сечения Z₁ = H, V₁ = 0, для второго сечения Z₂ = 0, V₂ = V_c. Тогда уравнение Бернулли приобретает вид

H = ,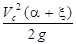

где V_c – скорость жидкости в сжатом сечении;

α – коэффициент неравномерности распределения скоростей по сечению.

Решив уравнение относительно V_c, получим

V_c = .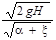

Расход жидкости тогда составит

Q = V_c S_c,

где S_c – площадь сжатого сечения.

Имея в виду, что пользоваться величиной площади сжатого сечения неудобно, перейдем к площади отверстия, используя коэффициент сжатия струи

S_c = S_отв ε.

Тогда расход жидкости через отверстие

.

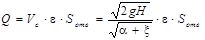Обозначим .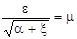

Формула расхода примет вид

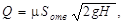
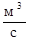, (104)

где μ – коэффициент расхода малого отверстия, изменяющийся в пределах ;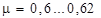

Н – напор, под действием которого происходит истечение жидкости.

При истечении жидкости через отверстия наблюдается явление, которое называется инверсией струи – изменение формы живого сечения струи при удалении от отверстия. Инверсия обусловлена действием сил поверхностного натяжения. Примеры инверсий трех типов струй приведены на рисунке 25.

Иногда в практике встречаются процессы истечения жидкости через затопленное отверстие под уровень жидкости Н₂. При условии, что положение свободных поверхностей жидкости не изменяется и давление на них равное (например, атмосферное).

Рис. 25. Инверсия струй

Расход жидкости через такое отверстие уменьшается, так как уменьшается напор Н₁ на величину Н₂

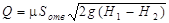, м³/с. (105)

Иногда требуется рассчитать время истечения заданного объема жидкости. Если напор (Н) при этом не изменяется, то время можно рассчитать как разность от деления объема на секундную производительность отверстия

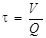, с. (106)

При изменении напора от Н до нуля, то есть при опорожнении (или заполнении резервуара) средний напор будет равен 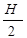, и время истечения соответственно увеличивается.

При затоплении одного из отсеков забортной водой через донное отверстие с одновременным изменением осадки предполагаемое время заполнения можно рассчитать по формуле

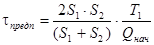, с, (107)

здесь Т₁ – начальная осадка (напор), м;

Q_нач- поступление воды в отсек через отверстие в первую секунду (при

Т₁);

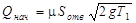, м³/с.

S₁ и S₂ – площади горизонтальных сечений отсека и всего плавсредст-

ва, м².