Классификация трубопроводов и их расчеты

При эксплуатации гидравлических систем возникают два режима (установившийся и неустановившийся) движения рабочих сред: воды, топлива, масел, пара, продуктов сгорания топлива, воздуха и т.д. Неустановившийся режим характеризуется резкой сменой давлений и скоростей в произвольном живом сечении потока с течением времени. Это можно наблюдать в периоды пуска и остановки насосов или компрессоров, регулировки режима с помощью запорно-регулирующей арматуры, в процессе циклической подачи топлива или масла в цилиндры ДВС. Однако большинство систем подавляющее количество времени эксплуатируется в установившемся режиме, поэтому основные приемы расчетов относятся именно к этому случаю.

Гидравлические системы – это совокупность труб различного диаметра, которые различаются характером соединения: последовательное, параллельное, разветвленное. Для удобства расчетов трубопроводы разделяют на простые и сложные, короткие и длинные.

Простые трубопроводы представляют собой последовательное соединение труб не обязательно одинакового диаметра, при условии постоянного расхода жидкости по длине. Сложные – это все остальные виды соединений труб, в том числе и последовательные с переменным расходом жидкости по длине.

Короткие трубопроводы – это такие, у которых местные потери соизмеримы с потерями напора по длине. При расчете длинных трубопроводов местными потерями напора можно пренебречь. Базовой расчетной зависимостью для любой системы является уравнение связи трех определяющих параметров: расхода жидкости Q (м³/с) и напора Н (м), которые обеспечивает насос, и диаметра трубопровода d (м). Поэтому возможны три постановки задачи: рассчитать Н по известным Q и d; определить Q по известным H и d; найти d по известным Q и H.

Для определения необходимого напора суммируют все потери напора

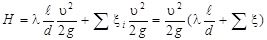. (109)

При известных значениях расхода (Q) и диаметра трубопровода (d) скорость движения жидкости можно определить как 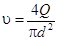, и тогда расчетная зависимость для короткого трубопровода приобретает вид

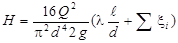. (110)

Расчетная зависимость для длинных трубопроводов имеет более простой вид

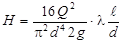. (111)

Полученное значение напора увеличивают обычно на 5…8%. Для другой постановки задачи – определения Q по известным H и d, необходимо уравнение (110) или (111) решить относительно Q

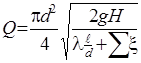. (112)

Однако в связи с тем, что расхода неизвестен, невозможно рассчитать скорость для определения коэффициента гидравлического трения, значением которого необходимо задаться. После определения расхода необходимо проверить корректность полученного результата.

Третья задача – определение диаметра (d) по известным значениям расхода (Q) и напора (Н) - может быть решена только графоаналитическим методом. Для этого следует выбрать несколько значений d и для каждого из них с помощью базовой зависимости (110) или (111) найти значения напоров при заданном значении Q. После этого строится график зависимости d = f(H), с помощью которого по известному значению напора находится необходимая величина d. Однако трубы изготавливаются промышленностью в соответствии с сортаментом и поэтому найденное значение диаметра необходимо увеличить до ближайшего большего по сортаменту.

Расчет сифонов

Сифон – это короткий трубопровод, по которому жидкость двигается из питающего резервуара в приемную емкость. Особенностью сифона является его способность поднимать жидкость в трубопроводе на высоту h выше ее уровня в питающем резервуаре. Принцип действия сифона основан на создании

Рис. 27. Перекачка жидкости сифоном

вакуума в верхней части сифона. Для включения сифона в работу необходимо предварительно заполнить его жидкостью или создать в нем вакуум с помощью специального вакуум-насоса. Расчет сифона состоит в определении его производительности или максимально возможной высоты транзитного подъема жидкости над уровнем жидкости в питающем резервуаре. Движущей силой процесса истечения жидкости через сифон является разность уровней жидкости в резервуарах, которая расходуется на преодоление сопротивлений (местных и по длине)

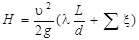, (113)

где L – суммарная длина трубы сифона, м;

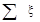- сумма коэффициентов местных сопротивлений.

Отсюда .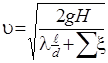

Тогда

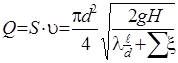. (114)

Максимально возможная высота сифона h определяется из уравнения Бернулли для сечений 1-1 и 2-2

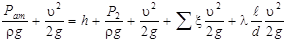, (115)

здесь 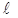- длина трубопровода до сечения 2-2;

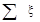- сумма коэффициентов местных сопротивлений до сечения 2-2.

Отсюда

,

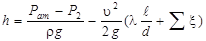здесь .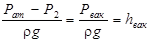

И тогда ,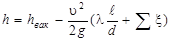

где Р_вак – вакуум, возникающий в сечении 2-2.

Теоретически возможная высота h_вак = 10,33 м водяного столба. Однако, учитывая потери энергии в сифоне, а также возможность возникновения явления кавитации, значение h_вак не должно превышать 7 – 8 м.