Методы расчета речного стока
Основным и надежным методом гидрологических оснований для установления характеристик речного стока служит метод непосредственных гидрологических наблюдений на данном гидростворе реки за длительный период времени. Однако не все наши реки располагают длительным рядом наблюдений. Кратковременные же наблюдения не могут служить надежной базой для гидрологических обоснований. Поэтому существует второй метод расчета стока для бассейнов с кратковременным рядом наблюдений -метод рек-аналогов и створов-аналогов путем приведения их к многолетнему ряду.
В этом методе используются материалы долговременных наблюдений в других створах данной реки или на соседних реках, протекающих в родственных физико-географических и климатических условиях. При выборе рек-аналогов учитываются однородность формирования стока, однотипность почв (грунтов) и гидрогеологических условий, по возможности близкую степень озерности, залесенности, заболоченности и распаханности. Площади водосборов должны отличаться не более чем в 10 раз.
Наконец, возможны и такие случаи, когда гидрометрические наблюдения в данном бассейне реки полностью отсутствуют. В этом случаи используют эмпирические формулы и карты изолиний различных характеристик стока, построенные на основании обобщений гидрометрических наблюдений для больших физико-географических районов (например, формула (1.25) и рис. 1.14 и 1.15).
Гидрологические характеристики зависят от множества еще до конца не изученных факторов и на современном этапе нельзя установить их ясно выраженную закономерность и закон изменения в многолетнем разрезе. Поэтому гидрологические величины можно рассматривать как случайные величины и применять к ним методы теории вероятностей и математической статистики.
Основой расчета годового стока воды рек при наличии достаточно продолжительных и репрезентативных рядов наблюдений являются кривые обеспеченности, показывающие вероятность превышения в процентах или долях единицы данной величины среди общей совокупности ряда.
Эмпирическая обеспеченность величины среднегодового расхода (%) определяется по формуле
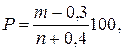 (1.18)
(1.18)
где m – порядковый номер члена ряда величины стока, расположенного в убывающем порядке; n – общее число членов ряда.
Для максимальных расходов талых и дождевых паводков обеспеченность рассчитывается по формуле
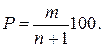 (1.19)
(1.19)
В качестве примера в таблице (1.3) приведен расчет параметров кривой распределения модульного коэффициента. При определении обеспеченности расчетной величины (в данном примере модуля стока Мi) ее величина располагается в убывающем порядке. По данным таблицы строится кривая обеспеченности модульного коэффициента (рис.1.12).
При отсутствии или недостаточности фактических данных по режиму реки кривые распределения стока могут быть построены теоретическим путем при помощи методов математической статистики. В гидрологии при построении теоретических кривых обеспеченности обычно применяется биномиальный закон распределения (гамма-распределение) случайной величины. Параметрами биномиального закона распределения являются среднеарифметическое значение ряда Хср, коэффициент вариации или изменчивости ряда Сv, коэффициент асимметрии Сs.
Коэффициент вариации является мерой изменчивости ряда. Величина коэффициента вариации те6м больше, чем сильнее колебания стока реки за многолетний период. Коэффициент асимметрии является показателем асимметричности ряда. Он характеризует степень несимметричности расположения членов многолетнего ряда гидрологической величины (стока, расхода, уровня и др.) относительно среднеарифметического значения.
Допустим, что имеется ряд наблюденных гидрологических величин, например среднегодовых расходов воды: Х1, Х2,…Хn. Эти величины рассматриваются случайными, не зависящими друг от друга.
Среднеарифметическое значение членов ряда
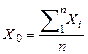 , (1.20)
, (1.20)
где n – число лет наблюдений.
Для характеристики отклонения членов ряда от среднеарифметического используется понятие среднего квадратического отклонения
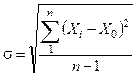 , (1.21)
, (1.21)
выражаемого в тех же единицах измерения, что и величина Хi.
Для удобства сравнения средние квадратические отклонения различных рядов выражаются в виде отвлеченных (безразмерных) величин. Поэтому вводится понятие коэффициента вариации или изменчивости ряда
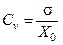 . (1.22)
. (1.22)
Коэффициент асимметрии вычисляют по формуле
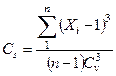 . (1.23)
. (1.23)
Величина коэффициента асимметрии принимаются кратной значению Сv. Обычно Сs = 2Сv (для рек северо-запада и северо-востока РФ Сs = 3Сv).
Для построения кривых обеспеченности необходимо вычислить ее ординаты при различных значениях обеспеченности по формуле
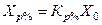 , (1.24)
, (1.24)
где Кр% – ордината кривой обеспеченности (или модульный коэффициент) при Х0 = 1, определяемая по таблице Крицкого и Менкеля в зависимости от коэффициента асимметрии Сs (приложение 1).
Таблица 1.3.
Расчет обеспеченности модульного коэффициента
| № п/п | Мi, л/(с∙км2) | P, % | Kм = Мi/M0 |
| 18,7 | 3,85 | 1,57 | |
| 16,3 | 7,69 | 1,37 | |
| 16,1 | 11,5 | 1,35 | |
| 15,2 | 15,4 | 1,28 | |
| 15,2 | 19,2 | 1,28 | |
| 14,9 | 23,1 | 1,25 | |
| 14,2 | 26,9 | 1,19 | |
| 13,6 | 30,1 | 1,14 | |
| 13,0 | 34,6 | 1,09 | |
| 12,8 | 38,5 | 1,08 | |
| 12,2 | 42,3 | 1,03 | |
| 11,9 | 46,2 | 1,00 | |
| 10,8 | 50,0 | 0,91 | |
| 10,8 | 53,8 | 0,91 | |
| 10,8 | 57,7 | 0,91 | |
| 10,2 | 61,5 | 0,86 | |
| 10,2 | 65,4 | 0,86 | |
| 10,0 | 69,2 | 0,84 | |
| 9,6 | 73,1 | 0,81 | |
| 9,6 | 76,9 | 0,81 | |
| 9,4 | 80,8 | 0,79 | |
| 9,3 | 84,6 | 0,78 | |
| 8,8 | 88,5 | 0,74 | |
| 7,9 | 92,3 | 0,66 | |
| 6,5 | 96,2 | 0,55 | |
| Среднее арифметическое значение модуля стока М0 = 11,9 л/(с∙км2). |
Рис. 1.13. Кривая обеспеченности среднегодового расхода
Практикой проектирования установлено, что осушительная сеть не должна рассчитываться на бесперебойную работу в любой многоводный год, а источник водоснабжения в любой засушливый год. Выполнение таких условий потребовало бы значительных затрат, поэтому, чтобы избежать омертвления капиталовложений допускают, что через определенное количество лет осушительная сеть в многоводные годы полностью не гарантирует нормальных условий добычи торфа, а источники водоснабжения в засушливые годы не обеспечивают требуемого потребления объема воды. В соответствии с нормами технологического проектирования предприятий по добыче торфа [7] обеспеченность расчетных расходов и уровней принимается по приложению 2.
При отсутствии наблюдений расчет расходов различной обеспеченности производится с помощью специальных карт, составленных Государственным гидрологическим институтом (ГГИ), для отдельных районов, а также по общим и региональным формулам[1,2] (рис 1.14,1.15).
Для расчетовмаксимальных расходов весеннего половодья равнинных рек Государственный гидрологический институт (ГГИ) рекомендует формулу, которая может быть использована при проектировании осушительных систем, расчета диаметра водопропускных труб и других гидротехнических сооружений [2]:
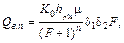 (1.25)
(1.25)
где Qвп – расчетный максимальный расход воды весеннего половодьяс вероятностью превышения Р, %, м3/c;
К0 – параметр, характеризующий дружность весеннего половодья, определяемый по табл. 1.4.
hр% – расчетный слой суммарного стока ежегодной вероятностью превышения Р, % (мм); определяется в зависимости от коэффициента вариации Сv и соотношения Cs/Сv, а также среднего многолетнего слоя стока половодья hо, устанавливаемого по рекам – аналогам или по карте (рис. 1.15). Обычно принимается Сs = 2Cv(для северо-запада и северо-востока РФ Сs = 3Cv); Коэффициент изменчивости слоя стока для водосборов более 200 км2 определяется по изолиниям на специальной карте (рис. 1.14); для бассейнов с F от 0 до 50 км2 к снятым с карты значениям вводится поправочный коэффициент 1,25; от 50 до 100 км2 – 1,25…1,20; от 100 до 150 км2 – 1,20. .1,15, от 150 до 200 км2 – 1,15…1,05.
μ – коэффициент, учитывающий неравенство статистических параметров слоя стока и максимальных расходов воды (определяется по табл. 1.5 [2];
n – показатель степени редукции (уменьшения) отношения qр/hр в зависимости от площади водосбора; определяется по таблице 1.4;
δ1– коэффициент, учитывающий снижение максимального расхода за счет зарегулирования стока озерами
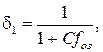 (1.26)
(1.26)
где С – параметр, зависящий от среднего слоя половодья (табл. 1.6):
Таблица 1.6
Величина параметра С вформуле (1.26)
| h0, мм | >100 | 100-50 | 50-20 | <20 |
| С | 0,2 | 0,2-0,3 | 0,3-0,4 | 0,4 |
fоз – озерность водосбора ( отношение суммы площади зеркал озер к площади водосбора реки, %). При озерности менее 2 % их регулирующее влияние не учитывается;
δ2 – коэффициент, учитывающий снижение максимального расхода воды за счет залесённости и заболоченности водосборной площади
δ2 = 1 – 0,8∙lg(1 + 0,05∙fл + 0,1 fб) , (1.27)
где fл – залесенность водосбора ( отношение площади, покрытой лесом к площади водосбора); %; fб - заболоченность водосбора ( отношение площади болот к площади водосбора, %.
При озерности более 20 % влияние залесенности и заболоченности не учитывается. Не принимается во внимание в расчетах максимальных расходов залесенность менее 5 % и заболоченность менее 3 %.
F – площадь водосбора, км2.
Таблица 1.4
Параметры n и К0 для равнинных рек
| Природная зона | Параметр n | Параметр К0 при категории рельефа | ||
| 1-я | 2-я | 3-я | ||
| Зона тундры и лесная зона | ||||
| Европейская территория РФ | 0,17 | 0,010 | 0,008 | 0,006 |
| Западная Сибирь | 0,25 | 0,015 | 0,013 | 0,010 |
| Лесостепная и степная зоны | ||||
| Европейская территория РФ | 0,25 | 0,30 | 0,017 | 0,012 |
| Западная Сибирь | 0,25 | 0,30 | 0,020 | 0,015 |
В качестве критерия определения категории рельефа в табл. 1.4 принимается параметр 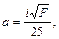 где i средневзвешенный уклон главного водостока, %; F – площадь водосбора.
где i средневзвешенный уклон главного водостока, %; F – площадь водосбора.
При а > 1,0 – 1-я, при а = 0,5 – 1,0 – 2-я, при а < 0,5 – 3-я категория рельефа.
>
Таблица 1.5
Значения коэффициента μ
| Природная зона | Обеспеченность, Р, % | |||||
| 0,1 | ||||||
| Зона тундры и лесная зона | ||||||
| Европейская территория РФ | 1,10 | 1,00 | 0,95 | 0,92 | 0,88 | 0,80 |
| Западная Сибирь | 1,04 | 1,00 | 0,98 | 0,96 | 0,94 | 0,88 |
| Лесостепная и степная зоны | ||||||
| При F > 200 км2 | 1,05 | 1,00 | 0,96 | 0,94 | 0,92 | 0,87 |
| При F < 200 км2 | 1,10 | 1,00 | 0,93 | 0,87 | 0,79 | 0,64 |
Рис. 1.14. Карта изменчивости слоя стока половодья рек (Сv)
Рис. 1.15. Карта среднего слоя стока половодья (h0, мм)
Пример 1.1.: Определить расчетный слой суммарного весеннего стока и расход весеннего половодья с ежегодной вероятностью превышения Р = 5% для створа магистрального канала осушительной системы торфяного месторождения с площадью водосбора 25 км2, расположенного в Тверской области.
1. По карте (рис. 1.15) определяем средней сток половодья h0 = 110 мм.
2.Определяем модульный коэффициент ежегодной вероятностью превышения Р = 5%. Предварительно определяем коэффициент вариации Сv по карте (рис.1.14): Сv=0,40.
Принимаем, что Cs = 2Cv = 0,8.
Определяем модульный коэффициент при обеспеченности 5% по таблице приложения 1: К5% = 1.74.
3. Определяем слой весеннего стока обеспеченностью Р = 5 % по формуле (1.24): h5% = ho×K5% = 110∙1,74 = 191,4 мм.
4. К0 – параметр, характеризующей дружность половодья; определяется по табл. 1.4 в зависимости от уклона главного водотока и площади водосбора.
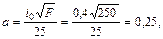
где i0 = 0,4 - средневзвешенный уклон главного водотока, %, определяется по топографическому плану торфяного месторождения
Тогда К0= 0,006.
5. Коэффициент μ,учитывающий неравенство статистических параметров слоя стока и максимальных расходов воды равен0.92 (табл. 1.5).
6. Показатель степени редукции n = 0,17 (табл. 1.4)
7. Пусть fл = 50 %, fб = 10 % , озерность водосбора менее 2 %. Тогда δ1 =1, а δ2= 1 – 0,8∙lg(1 + 0,05×50 + 0,1×10) = 0,48.
8. Вычислим расчетный расход весеннего паводка обеспеченностью Р = 5%.

Максимальные расходы воды дождевых паводков образуются в летне-осенний период во время выпадения обильных дождей. В зависимости от площади водосбора при отсутствии данных гидрометрических наблюдений и рек-аналогов они определяются по эмпирической редукционной формуле. Эмпирическая редукционная формула для тундровой, лесной и лесостепной зон применяется при площади водосбора от 50 до 50000 км2 и имеет вид [2]:
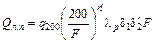 , (1.28)
, (1.28)
где Qлп– максимальный расход летне-осеннего поводка, м3/с;
q200– модуль максимального мгновенного расхода воды ежегодной вероятности превышения Р = 1 %, приведенный к площади водосбора F = 200 км2, определяемый по карте, приведенной в[1]; для севера и северо-запада РФ q200 = 0,3...0,4 м3/(с∙км2);
λp – переходный коэффициент от 1% обеспеченности к расчетной: для центра и северо-запада Европейской части РФ для площади водосбора F ³ 100 км2 λ25% = 0,40; для F= 0,1 км2 λ25% = 0,21. n¢ – показатель степени редукции модуля максимального расхода. Для центра Европейской части РФ n = 0,30, для северо-запада – n¢ = 0,22.
δ1 – коэффициент учитывающий снижение максимального расхода за счет зарегулирования стока озерами, определяемый по формуле (1.26), но величина параметра «С» в этой формуле для дождевых максимумов в лесной и лесостепной зонах равна 0,2;
δ2¢ – коэффициент учитывающий снижение максимального расхода заболоченностью водосбора:
δ2¢=1 – 0,8lg(1+0,1∙fб) …………………………….(1.29)
Для площади водосбора тундровой и лесной зоны менее 50 км2 применяется формула предельной интенсивности дождевого стока, которая имеет вид:
Qлп = q1%φh1%δ1λpF , (1.30)
где q1% - максимальный модуль стока, определяемый по специальной таблице, приведенной в СН и П 2.01.14-83 [2];
φ – сборный коэффициент стока, определяется по специальной формуле
 , (1.31)
, (1.31)
где С2 – эмпирический коэффициент, принимаемый для лесной и тундровой зоны равным 1,2; φ0 – сборный коэффициент стока для водосбора F площадью 10 км2, со средним уклоном iв, равным 50 0/00 принимается по таблице, приведенной в [2]. Для лесной и тундровой зоны φ0 находится в диапазоне 0,23 – 0,56 в зависимости от типа почв; ns – параметр, принимаемый по таблице, приведенной в [2]. Для лесной и тундровой зоны ns находится в диапазоне 0,50 – 0,80 в зависимости от типа почв.
h1% – максимальный суточный слой осадков вероятностью превышения Р = 1 %, определяемый по данным ближайшей к бассейну исследуемого водотока метеорологической станции или по карте [2].
Ориентировочный расчет модуля стока летних поводков для стока с осушенных полей добычи торфа с вероятностью превышения Р = 25 % (л/(с∙га) может быть выполнен по формуле Ю.В. Краснова и В.Ф.Митина [4]
М25% = Мэл..25%∙K , л/(с×га), (1.32)
где Мэл. 25% = 1,25 л/(с∙га) – элементарный модуль стока;
К = 1 – 0,1lgF – поправочный коэффициент на площадь водосбора.
Пример 1.2. Определить расход летнего паводка с ежегодной вероятностью превышения Р = 25% для створа магистрального канала осушительной системы торфяного месторождения с площадью водосбора 25 км2 (2500 га), расположенного в Тверской области. При расчете использовать формулу Ю.В. Краснова и В.Ф.Митина (1.32).
Определяем поправочный коэффициент К на площадь водосбора
К = 1 – 0,1lgF = 1 – 0,1lg2500 = 0,66.
Вычислим модуль стока М25% = Мэл..25%∙K =1,25×0,66 = 0,825 л/(с×га).
Определим расход летнего паводка (высоких летних вод)
Qлп = М25%×F×10-3 = 0,825×2500×10-3 = 2,06 л/(с×га).
Меженные(летние) модули стока независимо от характера водосбора могут приниматься приближенно без расчета для: Смоленской области – 0,02 л/(с∙га); Ярославской, Тверской, Московской, Владимирской, Рязанской – 0,04 л/(с∙га); Нижегородской, Кировской, Костромской и Ивановской областей равными – 0,05 л/(с∙га).
Дата добавления: 2021-03-18; просмотров: 827;











