Корпускулярно-волновой дуализм. Гипотеза де Бройля

Физика атомов, молекул, а также атомных ядер и элементарных частиц изучается в квантовой механике. Объекты микромира, изучаемые квантовой механикой, имеют линейные размеры порядка 10^-6 – 10^{-13 см. Если частицы движутся со скоростями υ<<с, где с – скорость света в вакууме, то применяется нерелятивистская квантовая механика; при υ ≈ с – релятивистская квантовая механика.}

В основе квантовой механики лежат представления Планка о дискретном характере изменения энергии атомов и Эйнштейна о фотонах, характеризующих в определенных условиях состояния частиц микромира.

В результате углубления представлений о природе света выяснилось, что в оптических явлениях обнаруживается своеобразный дуализм. Наряду с такими свойствами света, которые самым непосредственным образом свидетельствуют о его волновой природе (интерференция, дифракция), имеются и другие свойства, столь же непосредственно обнаруживающие его корпускулярную природу (фотоэффект, явление Комптона).

В 1924 г. Луи де-Бройль выдвинул гипотезу, что каждый микрообъект обладает, с одной стороны корпускулярными характеристиками, а с другой волновыми (см. табл.1).

Таблица 1.

Корпускулярные свойства	Волновые свойства
Скорость	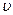Длина волны де Бройля 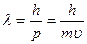Импульс фотона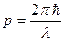
Импульс:	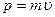Частота волны де Бройля 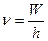Энергия фотона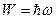
Энергия свободной частицы:	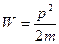Групповая скорость волн де Бройля 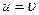Фазовая скорость волн де Бройля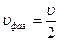

Фотон обладает энергией

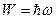
импульсом

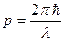
По идее де Бройля, движение электрона или какой-либо другой частицы связано с волновым процессом, длина волны которого равна

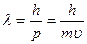
Формула де Бройля экспериментально подтверждается опытами по рассеянию электронов и других частиц на кристаллах и по прохождению частиц сквозь вещество. Впоследствии дифракционные явления были обнаружены также для нейтронов, протонов, атомных и молекулярных пучков. Это окончательно послужило доказательством наличия волновых свойств микрочастиц и позволило описать движение микрочастиц в виде волнового процесса, характеризующегося длиной волны, рассчитываемой по формуле де Бройля.