Определение грузоподъемности жесткого стержня моносимметричного сечения при внецентренном
Растяжении-сжатии (задача № 29)
Условие задачи
Жесткий стержень загружен двумя силами – растягивающей и сжимающей (рис. 5.21). Стержень выполнен из хрупкого материала с характеристиками 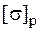 и
и 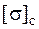 . Сечение стержня симметрично и имеет форму и размеры, соответствующие рис. 5.17. Требуется:
. Сечение стержня симметрично и имеет форму и размеры, соответствующие рис. 5.17. Требуется:
1) найти допускаемую нагрузку на стержень из условия прочности, если отношение сжимающей и растягивающей сил 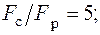
2) построить ядро сечения.
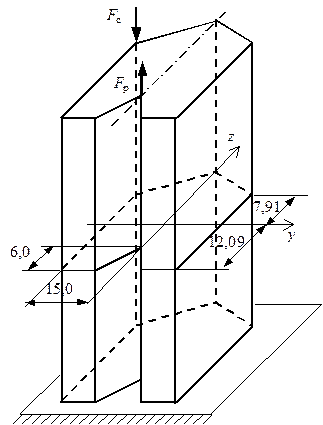 Рис. 5.21. Стержень, подверженный
растяжению-сжатию двумя силами
Рис. 5.21. Стержень, подверженный
растяжению-сжатию двумя силами
|
Решение
Положение главных центральных осей инерции и моменты инерции относительно этих осей заданного сечения найдены ранее в п. 5.2.1 (пример 1). Найдем внутренние усилия в произвольном сечении стержня:
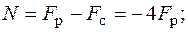
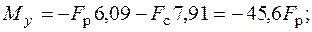
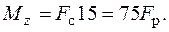
Для определения положения опасных точек построим нейтральную линию. Уравнение нейтральной линии (5.2) в данной задаче имеет вид
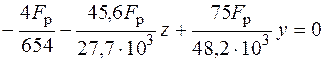 ,
,
или
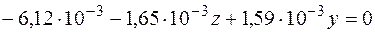 .
.
Отсюда найдем отрезки, отсекаемые нейтральной линией на осях 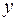 и
и 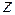 . Если
. Если 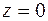 , то
, то
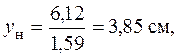
и, если 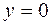 , то
, то
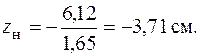
 Рис. 5.22. Эпюра напряжений от действия сил Fр и Fс и ядро сечения
Рис. 5.22. Эпюра напряжений от действия сил Fр и Fс и ядро сечения
|
Нейтральная линия показана на рис. 5.22. Проведем касательные к контуру сечения, параллельные нейтральной линии. Опасными являются точки 1 и 1¢ (см. рис. 5.22), наиболее отдаленные от нейтральной линии. Для хрупкого материала более опасной является точка с максимальными растягивающими напряжениями, т. е. точка 1. Найдем напряжение в этой точке, подставляя в формулу (5.1) координаты точки 1:
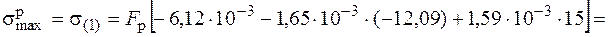
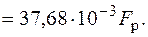
Условие прочности в точке 1 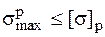 , или
, или
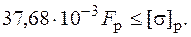
Отсюда можно найти допускаемое значение нагрузки[8]. В заключение необходимо убедиться в том, что и в точке 1¢, которая в данном примере дальше удалена от нейтральной оси, чем точка 1, и в которой действуют сжимающие напряжения, условие прочности тоже выполняется, т. е.
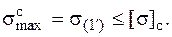
Теперь построим ядро сечения. Поместим полюсы во внешних угловых точках сечения. Учитывая симметрию сечения, достаточно расположить полюсы в трех точках: 1, 2 и 3 (см. рис. 5.22). Подставляя в формулы (5.12) координаты полюсов, найдем отрезки, отсекаемые нейтральными линиями на осях 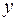 и
и 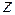 . Если полюс находится в точке 1, то его координаты
. Если полюс находится в точке 1, то его координаты 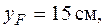
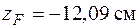 и
и
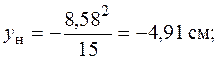
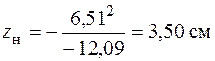 .
.
Нейтральная линия 1–1, соответствующая полюсу в точке 1, показана на рис. 5.22. Аналогично строим нейтральные линии 2–2 и 3–3, соответствующие полюсам 2 и 3. При построении нейтральной линии следите за тем, чтобы она проходила в квадранте, противоположном тому, в котором находится полюс. Область, заштрихованная на рис. 5.22, является ядром сечения. Для контроля на рис. 5.22 показан эллипс инерции. Ядро сечения должно находиться внутри эллипса инерции, нигде не пересекая его.
Дата добавления: 2016-11-29; просмотров: 1578;











