Таврового профиля с одиночной арматурой по нормальным сечениям

Расчетные формулы прочности нормальных сечений любой симметричной формы вводят из условия равновесия элемента в предельном состоянии ΣМ=0 и ΣХ=0.

В случае одиночного армирования ненапрягаемой арматурой уравнение ΣХ=0 можно записать в следующем виде:

R_bA_bc=R_sA_s (2.1)

Уравнение ΣМ=0 записывают в таком виде:

М≤М_u= R_bA_bcz_b=R_bS_bc (2.2)

Для прямоугольных сечений (рисунок 2.20) расчетные формулы прочности нормальных сечений получают из уравнений (2.1, 2.2) путем подстановки в них геометрических характеристик прямоугольных сечений:

А_b=bx; z_b=h_o-0,5x; S_b= А_b z_b =bx(h_o-0,5x) (2.3)

R_bbx= R_sA_s; x= R_sA_s/(R_bb)

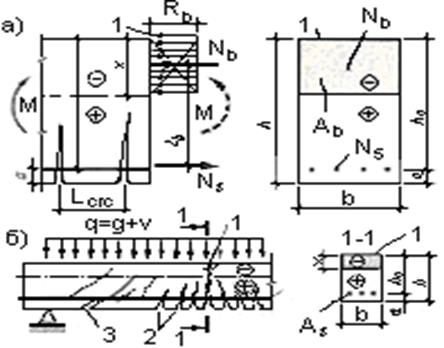Рисунок 2.20 - К расчету изгибаемых элементов

а – схема напряжений и усилий; б –схема разрушения

ζ=x/h_o= R_sA_s /(R_bbh_o); M≤R_bbx(h_o-0,5x) (2.4)

где ζ – относительная высота сжатой зоны.

Удобно пользоваться также выражением моментов, взятых относительно оси, проходящей через центр тяжести сжатой зоны:

M≤R_sA_s(h_o-0,5x) (2.5)

Формулы (2.3), (2.4) или (2.5) применяют совместно. Они действительны при x<ζ_Rh_o, где ζ_R– граничная относительная высота сжатой зоны, при которой растягивающие напряжения в арматуре начинают достигать предельных значений σ_s→R_s.

ζ_R= x_R/h_o =ω/{1+σ_sR/σ_scu (1-ω/1,1)} (2.6)

При одной и той же несущей способности элемента сечение арматуры получается тем меньше, чем больше рабочая высота сечения h_o. Следовательно, можно получить сечения элементов с большим и меньшим

содержанием арматуры.

Коэффициент армирования

μ=A_s/(bh_o) (2.7)

и процент армирования μ100 с учетом соотношений bxR_b= R_sA_s и ζ=x/h_o могут быть представлены следующим образом:

μ=ζR_b/R_s; 100μ=100ζR_b/R_s (2.8)

Отсюда можно установить максимально допустимое содержание арматуры в прямоугольном сечении по предельным значениям ζ_R.

Тавровые сечения часто встречаются как самостоятельные конструктивные элементы или в составе сборных, монолитных или сборно-монолитных конструкций. Тавровое

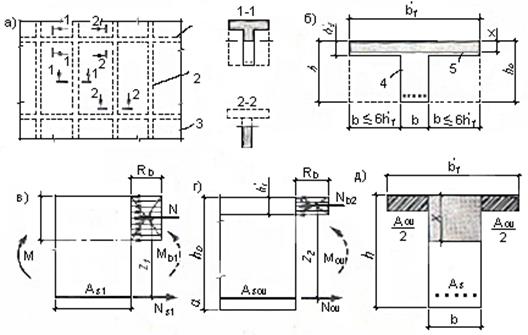
сечение элемента состоит из полки и ребра и имеет, как правило, одиночное армирование (рисунок 2.21).

Рисунок 2.21- Тавровое сечение

В сравнении с прямоугольным тавровое сечение значительно выгоднее, т.к. при одной и той же несущей способности расходуется меньше бетона вследствие сокращения размеров растянутой зоны.

При большой ширине полок участки свесов, более удаленные от ребра, напряжены меньше. Поэтому в расчет вводят эквивалентную ширину свесов полки b'_f, ограничивая ее значение при расчете согласно нормам.

Если нижняя граница сжатой зоны располагается в пределах полки (рисунок 3.11 б), то тавровое сечение рассчитывают как прямоугольное с размерами b'_f и h_o, поскольку площадь бетона в растянутой зоне на несущую способность не влияет.

Расчетные формулы (для элементов без предварительного напряжения):

R_b b'_f x = R_sA_s (2.9)

M≤R_b b'_f (h_o-0,5x) или M≤α_m R_b b'_f h_o² (2.10)

Когда нижняя граница сжатой зоны размещается ниже полки, то в этом случае сжатая зона сечения состоит из сжатых зон ребра и свесов полки.

Положение нижней границы сжатой зоны определяется из уравнения

R_sA_s=R_bbx+R_b(b'_f-b)h'_f (2.11)

Условие прочности при моментах, проходящих через точку приложения равнодействующей усилий в растянутой арматуре, имеет следующий вид:

M≤R_b bx (h_o-0,5x) +R_b(b'_f - b) h'_f(h_o – 0,5 h'_f) (2.12)

Для тавровых сечений должно быть соблюдено условие x≤ζ_Rh_o.