Представление ЦСК в виде параллельно-последовательной схемы

Структурно - логические схемы надежности позволяют графически отобразить взаимосвязь элементов цифровой системы коммутации и их влияние на работоспособность системы в целом. Структурно - логическая схема представляет собой совокупность элементов, соединенных друг с другом последовательно или параллельно. Критерием для определения вида соединения элементов (последовательного или параллельного) при построении схемы является влияние их отказа на работоспособность ЦСК в целом. В общем случае работоспособность ЦСК – способность реализовать и поддерживать соединение между пользователями.

Последовательным (с точки зрения надежности) считается соединение, при котором отказ любого элемента приводит к отказу всей системы (см. рис. 3.1).

Параллельным (с точки зрения надежности) считается соединение, при котором отказ любого элемента не приводит к отказу системы, пока не откажут все соединенные элементы (см. рис.3.2).

Рисунок 3.1.Последовательное Рисунок 3. 2 Параллельное соединение

соединение элементов элементов

Расчеты показателей безотказности технической системы обычно проводятся в предложении, что как вся система, так и любой ее элемент могут находиться только в одном из двух возможных состояний - работоспособном и неработоспособном и отказы элементов друг от друга не зависят. Состояние системы (работоспособное или неработоспособное) определяется состоянием элементов и их сочетанием.

Последовательное соединение элементов в технике встречается наиболее часто, поэтому его также называют основным соединением.

Предполагая отказы элементов независимыми, вероятность одновременной безотказной работы «n» элементов определяется по теореме умножения вероятностей.

Вероятность совместного появления независимых событий равна произведению вероятностей этих событий:

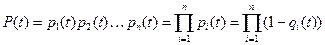, (3.1)

где pi(t) – вероятность того, что i-ый элемент в момент времени t находится в рабочем состоянии.

Соответственно, вероятность отказа такой системы

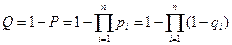. (3.2)

Если система состоит из «n» равнонадёжных элементов и р_i = р, то

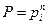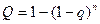, (3.3)

Из формул (3.1) - (3.3) видно, что даже при высокой надежности элементов надежность всей системы при последовательном соединении оказывается тем более низкой, чем больше число элементов

Кроме того, поскольку все сомножители в правой части выражения (3.1) не превышают единицы, вероятность безотказной работы системы при последовательном соединении не может быть выше вероятности безотказной работы самого ненадежного из ее элементов (принцип “хуже худшего”), и из малонадежных элементов нельзя создать высоконадежную техническую систему с последовательным соединением.

Если все элементы системы работают в периоде нормальной эксплуатации, и имеет место простейший поток отказов, наработки элементов и системы подчиняются экспоненциальному распределению и справедлива формула

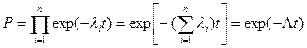, (3.4)

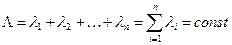(3.5)

где L - это интенсивность отказов системы. Таким образом, интенсивность отказов системы при последовательном соединении элементов и простейшем потоке отказов равна сумме интенсивностей отказов элементов.

Из (3.4) - (3.5) следует, что для системы из «n» равнонадёжных элементов, когда l_i = l, получаем

L=nl , 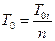, (3.6)

то есть интенсивность отказов в n раз больше, а средняя наработка до отказа в n раз меньше, чем у отдельного элемента.

Системой с параллельным соединением элементов называется система, отказ которой происходит только в случае отказа всех ее элементов. Такие схемы надежности характерны, например, для систем управления ЦСК, в которых элементы дублируются или резервируются, то есть параллельное соединение используется как метод повышения надежности.

Отказ всей системы заключается в совместном отказе всех элементов, вероятность чего (при допущении независимости отказов) может быть найдена по теореме умножения вероятностей как произведение вероятностей отказа элементов:

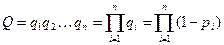. (3.7)

Соответственно, вероятность безотказной работы системы

. (3.8)

Для систем из «n» равнонадежных элементов при р_i = р запишем

Q=qⁿ , 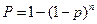. (3.9)

Надежность системы с параллельным соединением повышается при увеличении числа элементов (например, при р=0.9 и n=2 получаем Р=0.99, а при n=3 получаем Р=0.999).

Поскольку q_i <1, произведение в правой части (3.7) всегда меньше любого из сомножителей, то вероятность отказа системы не может быть выше вероятности самого надежного ее элемента (“лучше лучшего”) и даже из сравнительно ненадежных элементов возможно построение вполне надежной системы.

При экспоненциальном распределении наработки выражение (3.9) принимает вид

Р = 1 - [1 - ехр(- l t)]ⁿ , (3.10)

откуда после интегрирования и преобразований средняя наработка системы определяется как

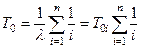, (3.11)

где Т_{0 i} = 1/l _i - средняя наработка i- ого элемента.

При больших значениях «n» справедлива приближенная формула

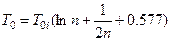. (3.12)

Таким образом, средняя наработка системы с параллельным соединением больше средней наработки ее элементов (например, при n = 2 получаем Т₀ = 1.5T_o, а при n = З получаем T₀ = 1.83T_0i).