Эпюры гидростатического давления.

Для решения многих практических задач приходится строить эпюры гидростатического давления, которые представляют собой графические изображения распределения гидростатического давления на плоские прямоугольные поверхности. Эпюра помогает уяснить характер неравномерности передаваемого от жидкости на стенку давления.

Рассмотрим случай определения гидростатического давления на плоскую вертикальную стенку АВ, шириной СВ, на которую давит жидкость с плотностью ρ и высотой h (рисунок 5).

Для этого воспользуемся основным уравнением гидростатики

Р_абс = ρqh + Р_а

Это уравнение гидростатического давления по глубине и является уравнением прямой.

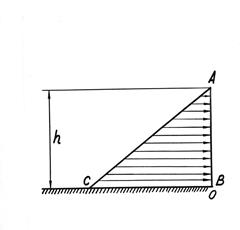Рисунок 5

Следовательно, для построения эпюры гидростатического давления, действующего на стенку, необходимо знать две точки: гидростатическое давление на поверхность жидкости и у днища резервуара.

Избыточное давление на поверхности жидкости равно нулю, т.к.

Р_абс = Р_а

У днища резервуара избыточное давление

Р_изб = ρqh

Приняв за начало координат точку 0 и отложив в выбранном масштабе из точки 0 величину

Р_изб = ρqh

перпендикулярно стенке АВ (согласно первому свойству гидростатического давления) соединяем полученную точку С с точкой А прямой линией. Треугольник АВС называют эпюрой избыточного давления на плоскую вертикальную стенку.

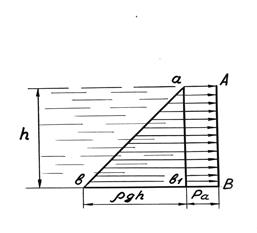Эпюра абсолютного гидростатического давления на стенку АВ изобразится трапецией АавВ (рисунок 6), состоящей из прямоугольника Аав₁В, ширина которого Аа и Вв₁, выраженная в масштабе, представляет собой атмосферное

Рисунок 6

давление и треугольника авв₁, представляющего характер изменения избыточного давления ρqh по глубине резервуара, выраженного в том же масштабе, что и атмосферное давление.

Так как атмосферное давление оказывает воздействие на открытую свободную поверхность жидкости и на стенки сосуда (резервуара) с внешней стороны, то действие его уравновешивается. Поэтому в технических расчетах чаще всего определяют избыточное гидростатическое давление

Р_изб = ρqh

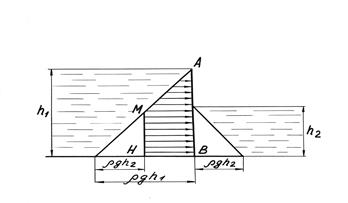Рассмотрим эпюру избыточного гидростатического давления для вертикальной плоскости АВ, подверженной действию жидкости с двух сторон (рисунок 7).

Рисунок 7

В данном случае на стенку АВ будут действовать параллельные и противоположно направленные силы гидростатического давления.

Поэтому силы, действующие справа налево, будут вычитаться из сил, действующих слева направо.

Получающаяся в результате эпюра представляет собой вертикальную трапецию.

Эпюра гидростатического давления на горизонтальное плоское днище резервуара представляет собой вертикальный прямоугольник (рисунок 8), так как при постоянной глубине избыточное гидростатическое давление на днище является постоянным.

P_изб= ρqhω_дн

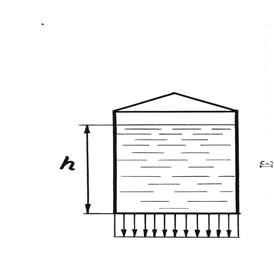Рисунок 8

В случае, когда сосуд имеет наклонную стенку, составляющую с горизонтальной плоскостью некоторый угол α, эпюра избыточного гидростатического давления представляет собой прямоугольный треугольник (рис.9) АbВ, в котором отрезки, изображающие давления, наклонены к горизонтальной плоскости под углом 90⁰.

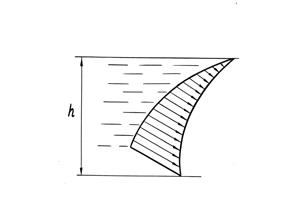Рисунок 9

На рисунке 10 изображены три сосуда различной формы, заполненные одинаковой жидкостью на одинаковую высоту h и во всех трёх сосудах площадь дна одинакова.

В каком сосуде будет больше сила гидростатического давления на дно сосуда?

(Проблемный вопрос).

В лекции отмечалось, что, если стенка расположена горизонтально, т.е. представляет собой не боковую стенку, а горизонтальное дно резервуара, то суммарное давление на дно резервуара определится по формуле

Р_изб= ρqhω

где h—глубина жидкости в резервуаре.

Следовательно, давление на дно резервуара (сосуда) зависит не от формы объёма жидкости в нём, а только от площади дна и глубины жидкости в сосуде. Поэтому для сосудов разной формы (рисунок 12), заполненных одной и той же жидкостью до одного и того же уровня h и имеющих одинаковую площадь дна, сила полного гидростатического давления на дно будет одинакова.

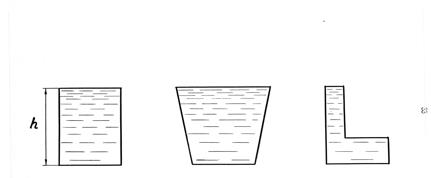Рис.12

Это явление известно под названием гидростатического парадокса.

Оно было впервые открыто итальянским физиком Галлилеем (1564-1642гг.) Это явление также известно как второй закон французского физика Паскаля (1623-1662гг.).