Вывод по первому вопросу
Неустановившееся течение жидкости
В жестких трубах
Неустановившееся течение жидкости это такое течение, все характеристики которого (или некоторые из них) изменяются во времени в точках рассматриваемого пространства.
В общем случае неустановившегося течения давление и скорость зависят как от координат, так и от времени:
Р = f (x, y, z, t)
Q = f (x, y, z, t)
Примером неустановившегося течения жидкости могут служить постепенное опорожнение сосуда через отверстие в дне.
 |
Так как неустановившееся течение жидкости в общем случае является достаточно сложным, то мы ограничимся здесь лишь основным частным случаем, с которым приходится сталкиваться в технике, - неустановившемся течением абсолютно несжимаемой жидкости в жесткой трубе постоянного сечения и в трубопроводе, составленном из ряда последовательно соединенных труб разных диаметров. Стенки труб при этом будем предполагать абсолютно жесткими.
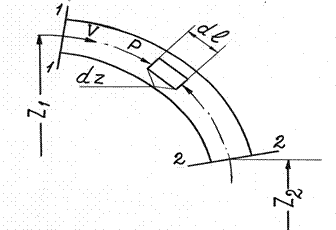
Рисунок 1. Схема неустановившегося течения в трубе.
Возьмем трубу длиной 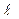 и диаметром d, произвольно расположенную в пространстве (рисунок 1), и обозначим нивелирные высоты начального (1-1) и конечного (2-2) ее сечений соответственно через Z1 и Z2. Пусть в этой трубе движется жидкость с ускорением, которое в общем случае может быть переменным по времени и равным
и диаметром d, произвольно расположенную в пространстве (рисунок 1), и обозначим нивелирные высоты начального (1-1) и конечного (2-2) ее сечений соответственно через Z1 и Z2. Пусть в этой трубе движется жидкость с ускорением, которое в общем случае может быть переменным по времени и равным
 j =
j = 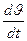 (1)
(1)
Очевидно, что в данный момент времени скорость 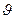 и ускорение j являются одинаковыми для всех поперечных сечений трубы.
и ускорение j являются одинаковыми для всех поперечных сечений трубы.
Потерями энергии на трение вначале будем пренебрегать, а распределение скоростей по сечениям будем считать равномерным.
Выделив из движущегося в трубе объема жидкости элементарный цилиндрический объем длиной dl и площадью основания dS (рисунок 1), составим уравнение его движения.
Проектируя силы давления и силу тяжести на направление касательной к оси трубы, (учитывая, что р есть функция не только l, но и t) проведя математические преобразования, получим
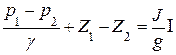 (2)
(2)
или
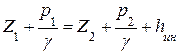 , (3)
, (3)
где
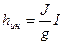 (4)
(4)
Полученное уравнение сходно с уравнением Бернулли для относительного движения в трубопроводе постоянного сечения, а член 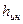 также называется инерционным напором, однако, путать
также называется инерционным напором, однако, путать 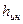 с
с 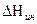 не следует, так как они имеют разный смысл. Величина
не следует, так как они имеют разный смысл. Величина 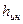 , как это видно из уравнения (30), представляет собой разность удельных потенциальных энергий жидкости в сечениях 1-1 и 2-2 в данный момент времени, обусловленную ускорением (или торможением) потока жидкости в трубе. При ускорении эта разность положительна, т.е. удельная энергия жидкости вдоль потока уменьшается, а при торможении – отрицательна, что означает увеличение удельной энергии жидкости от сечения 1-1 к сечению 2-2.
, как это видно из уравнения (30), представляет собой разность удельных потенциальных энергий жидкости в сечениях 1-1 и 2-2 в данный момент времени, обусловленную ускорением (или торможением) потока жидкости в трубе. При ускорении эта разность положительна, т.е. удельная энергия жидкости вдоль потока уменьшается, а при торможении – отрицательна, что означает увеличение удельной энергии жидкости от сечения 1-1 к сечению 2-2.
При наличии гидравлических потерь энергии в трубе (местных и на трение) они должны быть записаны в правой части уравнения (3):
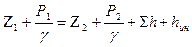 (5)
(5) 
Уравнение (5) справедливо лишь для трубы постоянного сечения. Если же трубопровод состоит из нескольких участков с разными площадями сечений 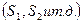 , то очевидно, что инерционный напор для всего трубопровода должен быть найден как сумма инерционных напоров для каждого участка. При этом соответствующие ускорения определяются из следующих уравнений, представляющих собой результат дифференцирования уравнений расхода по времени,
, то очевидно, что инерционный напор для всего трубопровода должен быть найден как сумма инерционных напоров для каждого участка. При этом соответствующие ускорения определяются из следующих уравнений, представляющих собой результат дифференцирования уравнений расхода по времени,
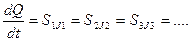
Кроме того, как это следует из приведенных выше энергетических соображений, в этом случае следует учесть скоростные напоры в начальном и конечном сечений трубопровода.
Вывод по первому вопросу
Таким образом, уравнение неустановившегося течения жидкости между сечениями c учётом инерции жижкостиимеет вид
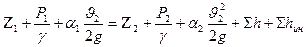 (6)
(6)
Дата добавления: 2016-11-29; просмотров: 1394;











