Механизм действия ферментов
Большую роль в развитии представлений о механизме действия ферментов сыграли классические работы Михаэлиса и Ментен, которые развили положения о Е-S-х комплексах. Согласно их представлениям (1915г.), ферменты обратимо соединяются со своим S, образуя нестойкий промежуточный продукт – Е-S-комплекс,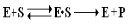 
который в конце реакции распадается на ферменты и продукты реакции (Р). Фактически в природе идет ступенчатое превращение S через целый ряд промежуточных реакций: ES1→ ES2→ ES3 … → E + P. Схематически преобразование S в Р можно представить таким образом:
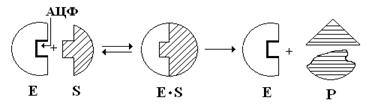
АЦФ, как правило, располагается в глубине молекулы Е.
Математическая обработка реакции образование ЕS-комплекса позволила вывести уравнение, которое называется уравнением Михаэлиса-Ментен:
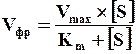
где Vфр – наблюдаемая скорость фр;
Vmax – максимальная скорость фр при неполном насыщении фермента S-том;
[S] – концентрация S;
Км – константа Михаэлиса-Ментен.
Графически уравнение Михаэлиса-Ментен имеет следующий вид:
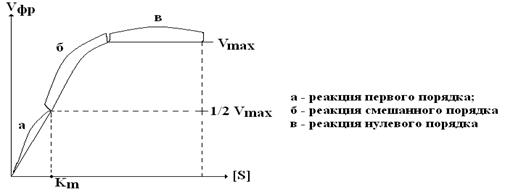
При низкой [S] Vфр прямо пропорциональна [S] в каждый данный момент времени (реакция 1-го порядка).
Из уравнения Михаэлиса-Ментен также следует, что при низком значении Км и высоком значении [S] Vфр является максимальной (в) и не зависит от [S] – это реакция нулевого порядка. Реакция нулевого порядка соответствует явлению, которое называется полным насыщением фермента субстратом.
Гипербола, выражающая зависимость Vфр от [S], называется кривой Михаэлиса. Чтобы правильно определить активность ферментов, нужно добиться реакции нулевого порядка, то есть определять Vфр при насыщающих концентрациях S.
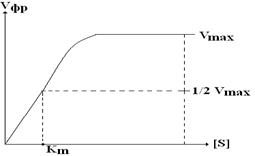
| Км численно равна [S] (моль(л)), при которой V реакции равна половине от максимальной. Для определения численного значения Км находят ту [S], при которой Vфр составляет от ½ от Vmax. Таким образом, определение Км играет важную роль для выяснения МД модификаторов на активность фермента. |
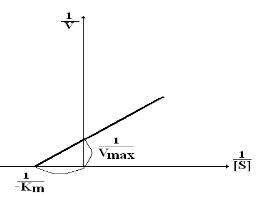
| Иногда график строят методом двойных обратных величин – метод Лайнуивера-Бэрка: Значение как Vmax, так и Км более точно определяется методом двойных обратных величин. |
ЛЕКЦИЯ 7
Дата добавления: 2016-11-29; просмотров: 1327;
Поиск по сайту
Узнать еще
- CIH — газораспределительный механизм с распределительным валом в головке блока цилиндров
- II группа действий. ВЗАИМОДЕЙСТВИЯ
- II. ОБУЧЕНИЕ ПРОСТЫМ БОЕВЫМ ДЕЙСТВИЯМ
- II. Получение вращающегося магнитного поля и принцип действия АД.
- II. Принцип действия и режимы работы синхронной машины
- II. Электрическая схема и принцип действия.
- III. БОЕВЫЕ ДЕЙСТВИЯ
- III. Механизмы регуляции количества ферментов
Публикации по технике и механике
Публикации по биологии
Публикации по информатике
Публикации по строительству
Публикации по физике
Публикации по химии
Публикации по электронике
Публикации по искусству
Публикации по истории
Публикации по медицине
