Многоканальный ранговый обнаружитель
Переход к ранговым тестам позволяет учитывать не только факт, но и степень отклонения элементов исследуемой выработки от некоторого уровня или элементов опорной выработке только шумовых сигналов значения ранга какого-либо элемента выборки. При наличии в выборке только шумовых сигналов значение ранга какого либо элемента выборки равновероятно, каково бы ни было распределение шума.
В ранговых обнаружителях предусматривается обязательный переход от выборочного вектора к ранговому
 , (4,24)
, (4,24)
где 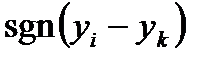 - элементы знакового вектора.
- элементы знакового вектора.
Число возможных комбинаций элементов m- мерного рангового вектора определяется числом перестановок m: целых чисел 1,2, . . ., m, что определяет большую информативность комбинаций рангового вектора.
На рис.4.21 изображена структурная схема многоканального рангового обнаружителя.
На схеме изображен ранговый обнаружитель для случая, когда опорная выборка формируется смежными каналами обнаружения, которые считаются «помеховыми». Работает обнаружитель следующим образом. Полезный сигнал находится в (m+1)-м элементе разрешения. Продетектированный сигнал (m+1)-го канала обнаружения Ui,m+1 (i- номер периода наблюдения) поступает на многоотводную линию задержки и далее на схемы сравнения (СС). В СС значение выборки Ui,m+1 сравнивается со всеми элементами опорной выборки Ui,1,…,Ui,m, накопленной в многоотводной линии задержки. Результаты сравнений hi,1,…,hi,m поступают на счетчик инверсий (СИ), который формирует ранг τi,m+1 отсчета Ui,m+1 в двоичном виде. Анологичным образом формируется все ранги элементов выборочного вектора. По всем накопленным за N ob период наблюдения значениям рангов вычисляется статистика S и сравнивается с порогом в пороговом устройстве (ПУ). Простейшей и наиболее употребительной ранговой статистикой является линейная по отношению к ранговому вектору и к ожидаемому сигналу статистика Вилкоксона
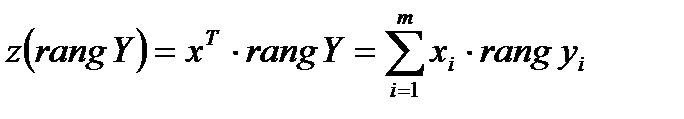 . (4.25)
. (4.25)
где xi - элементы выборочного вектора.
Если указанная сумма превысит порог, принимается решение об обнаружении.
Одним из возможных вариантов обнаружителя по критерию ранговой суммы для РЛС с k элементами разрешения может быть следующий.
Зона обнаружения РЛС разбивается на отдельные дискреты по дальности и азимуту. Обозначим соответствующие элементы дальности через i, а азимута через j. Компоненты xi1, xi2, …, xik для i-го импульса ранжируются так, чтобы получить ранговый вектор ri1, ri2, …, rik, где rij – ранг компоненты kij. После общего числа п импульсов формируется k сумм вида
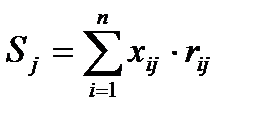 , (4.26)
, (4.26)
где j = 1, 2, …, k.
Если Sj превысит установленный порог, вырабатывается решение об обнаружении сигнала.
Упрощенным вариантом обнаружителя по критерию ранговой суммы является обнаружитель с квантованием рангов (с ранговым квантованием – РК), который работает следующим образом. Вместо ранжирования данных, получаемых от каждого импульса, q наибольших значений из xi1, xi2, …, xik заменяются единицами, а остальные значения – нулями. Эти единицы и нули суммируются по отдельности для каждого элемента разрешения, и если при этом превышается порог, то принимается решение, что в данном элементе сигнал присутствует.
Структурная схема цифрового обнаружителя сигнала с известными параметрами на основе линейной ранговой статики Вилкоксона показана на рис.4.22.
Рис. 4.22. Цифровой ранговый обнаружитель.
Ни одна из описанных процедур не является оптимальной и, следовательно, вероятностные характеристики обнаружения ухудшаются. На рис.4.23 изображена зависимость вероятности обнаружения от отношения сигнал/шум для различных алгоритмов обнаружения, при F=10-6
Рассмотренные выше обнаружители относятся к обнаружителям с фиксированным объемом выборки. Существуют и обнаружители последовательного типа, алгоритм работы которых базируется на вычислении отношения правдоподобия на основе рангов наблюдений.
Для вычисления отношения правдоподобия необходимо принять в качестве исходных данных некоторые совместные функции распределения для случаев, когда присутствует только шум или смесь сигнала и шума.
Ранговые обнаружители обладают следующими свойствами:
1. Большая информативность комбинаций рангового вектора.
2. Любое монотонное неубывающее преобразование элементов выборочного вектора не изменяет рангового вектора.
3. Ранговый обнаружитель обеспечивает постоянное значение условной вероятности ложной тревоги.
4. Ранговые обнаружители не реагируют на одновременное изменение уровней сигнала и помехи, что расширяет динамический диапазон обработки.
5. Ранговые алгоритмы инерционны: переход к рангам невозможен без запоминания всей выборки.
6. Переход от выборочных значений к их рангам приводит к потери части информации, но при увеличении объема наблюдений статистическая связь между ними растет.
Рассматриваемые алгоритмы обнаружения относятся к классу непараметрических. Алгоритмы этого класса составляют эвристически (изобретают) без жесткой фиксации ожидаемого распределения отсчетов помехи.
Их функционирование не сводится, поэтому, к учету параметров известных распределений.
Основным требованием к непараметрическому алгоритму считают фиксацию условной вероятности ложной тревоги F (без дополнительных регулировок уровня порога или усиления). Оказывается при этом, что знаковые алгоритмы асимптотически оптимальны для распределения отсчетов помех вида (рис.4.24, а), ранговые алгоритмы Ван-дер-Вардена – для гауссовских распределений отсчетов помех (рис.4.24, б), ранговые алгоритмы Вилкоксона – для промежуточных между ними распределений.
Параметрическое и непараметрическое обнаружение при использовании критерия Нймана-Пирсона требует стабилизации условной вероятности ложной тревоги.
Дата добавления: 2021-02-19; просмотров: 443;











