Задача Баклея - Леверетта и ее обобщения

В случае одномерного течения несжимаемых несмешивающихся жидкостей в условиях, когда можно пренебречь капиллярным давлением, а также влиянием силы тяжести, процесс вытеснения допускает простое математическое описание.

Для обоих случаев одномерного потока (прямолинейно-параллельного и плоскорадиального) это приводит к классической в теории вытеснения модели Баклея—Леверетта.

В рассматриваемом случае важное значение имеет так называемая функция Баклея - Леверетта или функция распределения потоков фаз f(s), которая имеет простой физический смысл. Действительно, данная функция представляет собой отношение скорости фильтрации вытесняющей фазы к суммарной скорости и равна объемной доле потока вытесняющей жидкости (воды) в суммарном потоке двух фаз. Таким образом, функция Баклея - Лаверетта определяет полноту вытеснения и характер распределения газоконденсатонасыщенности по пласту. Задачи повышения нефте- и газоконденсатоотдачи в значительной степени сводятся к применению таких воздействий на пласт, которые в конечном счете изменяют вид функции f(s) в направлении увеличения полноты вытеснения.

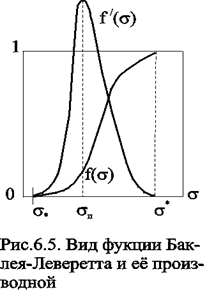
Вид кривых функции f(s) и ее производной f^/(s) показан на рис.6.5. С ростом насыщенности f(s) монотонно возрастает от 0 до 1. Характерной особенностью графика f(s) является наличие точки перегиба s_п , участков вогнутости и выпуклости, где вторая производная f^//(s) соответственно больше и меньше нуля. Эта особенность в большой степени определяет специфику фильтрационных задач вытеснения в рамках модели Баклея—Леверетта.

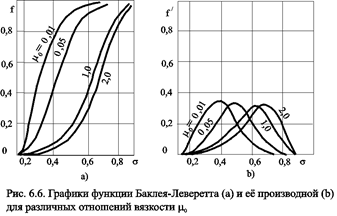
Зависимость функций f(s) и f^/(s) от отношения вязкостей фаз m₀=m₁/ m₂ показана рис. 6.6. Из данного рисунка следует, что с ростом отношения вязкостей кривая f(s) сдвигается вправо и эффективность вытеснения возрастает. Например, применение пен и загустителей, повышающих вязкость нагнетаемой воды, может значительно увеличить нефтеотдачу.

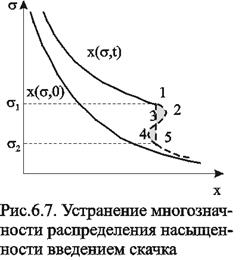
Физической особенностью модели двухфазного вытеснения Баклея – Леверетта является зависимость скорости распространения того или иного значения насыщенности от величины этой насыщенности. Это явление называется дисперсией волн. При 0£s£s_п большие насыщенности распространяются с большими скоростями, а при s_п<s£1 скорость распространения постоянного значения насыщенности начинает уменьшаться. Последнее приводит к тому, что, начиная с некоторого момента времени, распределение насыщенности оказывается многозначным (рис.6.7, кривая 1-2-3-4-5). В области данного участка одному и тому же значению х соответствуют три значения насыщенности s: s₁, s₂ и s₃, что физически невозможно, так как в каждом сечении пласта в любой момент времени может существовать только одна насыщенность. Данная неоднозначность устраняется введением скачка насыщенности (рис.6.7, отрезок 1-3-5). Скорость распространения скачка при этом равна скорости распространения насыщенности. Необходимо отметить, что в действительности математический скачок насыщенности не имеет места. Он появляется в решении вследствие пренебрежения капиллярными силами, за счет которых появляется некоторая “переходная зона” вблизи фронта вытеснения, в которой насыщенность изменяется непрерывно.

Точные решения задачи о вытеснении нефти (или газа) водой применяются при оценочных инженерных расчетах параметров разработки с использованием процесса заводнения.

В общем случае неодномерного вытеснения, а также при учете сжимаемости одной из фаз рассмотренная задача уже не сводится к одному уравнению для насыщенности. Необходимо совместно определять давление и насыщенность. Численные решения таких задач могут быть получены лишь на ЭВМ.