Элементарные логические функции
1) Конъюнкция (операция "и", логическое умножение). Конъюнкция нескольких переменных равна 1 лишь тогда, когда все переменные равны 1.Конъюнкция обозначается в виде произведения у = х1·х2, или у = х1х2, или у = х1Λх2. Обозначение элемента в схеме приведено на рис 2-1.
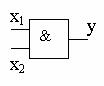
Рис.2-1 Конъюнктор
Таблица соответствия для конъюнкции
| х1 | х2 | у=х1·х2 |
Таблица 2 Конъюнкция
2) Дизъюнкция (операция "или", логическое сложение). Дизъюнкция нескольких переменных равна 1, если хотя бы одна из переменных равна 1. Дизъюнкция обозначается в виде суммы: у = х1+х2, или у = х1Vх2. Обозначение элемента в схеме приведено на рис.2-2.
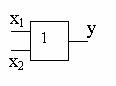
Рис.2-2Дизъюнктор
Таблица соответствия для дизъюнкции
| х1 | х2 | у=х1+х2 |
Таблица 3 Дизъюнкция
3) Инверсия (операция "не", логическое отрицание). Обозначение элемента в схеме приведено на рис 2-3.
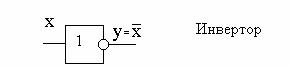
Рис.2-3
Таблица соответствия для инверсии
| х | у= 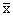
|
Возможны комбинированные операции. Примеры элементов,выполняющих такие действия приведены на рис.2-4.
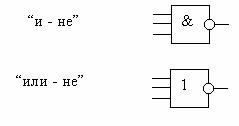
Рис. 2-4 Комбинированные логические элементы
4) Исключающее "или" – функция равна 1,когда только одна переменная равна 1. Обозначается значком 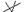
5) Сумма по модулю 2 - функция равна 1,когда нечетное число переменных равно 1, функция равна 0, когда четное число переменных равно 1. Функция обозначается: в виде у = Σmod2 = х1 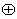 х2
х2 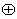 ...
... 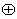 хn. Для двух переменных Σmod2 совпадает с функцией исключающее "или". Для трех переменных в таблице 4 приведены данные для функций "исключающее или" и "сумма по модулю 2". Они уже неполностью совпадают.
хn. Для двух переменных Σmod2 совпадает с функцией исключающее "или". Для трех переменных в таблице 4 приведены данные для функций "исключающее или" и "сумма по модулю 2". Они уже неполностью совпадают.
| х1 | х2 | х3 | у1=х1 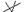 х2 х2 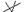 х3 х3
| у2=х1 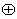 х2 х2  х3 х3
|
| 1 !!! |
Таблица 4 Сравнение функций
Система логических функций называется функционально полной, если используя только эти функции можно реализовать любые другие. Функционально полными являются системы:
1) "и", "или", "не";
2) "и", "не";
3) "или", "не".
Порядок выполнения логических операций: "не","и","или" (если нет скобок).
Дата добавления: 2016-11-29; просмотров: 4817;











