Уравнения электромагнитного поля в интегральной форме.

Нам уже известно, что электромагнитное поле – это особый вид материи,существующий как в связи с заряженными частицами, составляя с ними единое целое, так и в виде электромагнитных волн, или фотонов, движущихся со скоростью света.

Электромагнитное поле является носителем энергии, способной легко преобразовываться в другие виды энергии - механическую, тепловую, химическую, световую. Электромагнитное поле обладает и массой, величина которой чрезвычайно мала.

Кроме того, электромагнитное поле обладает особыми свойствами, оно оказывает силовое воздействие на заряженные частицы, пропорциональное заряду частицы и скорости ее движения. Только с помощью электромагнитного поля возможно ускорение и изменение траектории заряженных частиц.

Электрическое и магнитное поля – две стороныединого электромагнитного поля, которые неразрывно связаны между собой. В зависимости от изменения условий наблюдения может проявляться либо одна, либо другая его сторона.

Во всех случаях при наличии электрического тока возникает магнитное поле. Связь между электрическим током и напряженностью магнитного поля устанавливает закон полного тока(первое уравнение Максвелла):

.

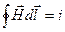Этот закон справедлив для любого замкнутого контура. Ток в правой части уравнения проходит сквозь площадку, ограниченную контуром интегрирования, и включает в себя как ток проводимости, так и токи переноса и смещения, в том числе и ток смещения в пустоте.

Существует еще один закон, устанавливающий связь между электрическим полем и изменяющимся магнитным полем, это закон электромагнитной индукции(второе уравнение Максвелла):

.

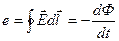При каждом изменении магнитного поля возникает связанное с ним электрическое поле.

Возникновение магнитного поля при появлении электрического тока, описываемое законом полного тока, было установлено экспериментально по действию на магнитную стрелку.. Попытки постановки эксперимента, иллюстрирующего закон электромагнитной индукции, долго оставались безуспешными. Даже великий Ампер, пытаясь установить возможность получения электрического поля с помощью магнитного поля, поставил в 1820 г. следующий опыт. Он подключил многовитковый соленоид к гальванометру, расположив его и соленоид в соседних комнатах, чтобы исключить возможность влияния манипуляций с соленоидом на гальванометр. Затем вносил постоянный магнит внутрь соленоида и переходил в соседнюю комнату, чтобы зафиксировать показания гальванометра. Никакого эффекта он не обнаружил. Аналогичный опыт 29 августа 1831 года осуществил Майкл Фарадей. Однако он работал с помощником, который по его команде вносил магнит в соленоид. Сам Фарадей в это время находился у гальванометра и зафиксировал отклонение его во время перемещения постоянного магнита. Тем самым был экспериментально установлен факт, подтверждающий наличие искомого эффекта – появление электрического поля при изменении магнитного поля.

Источником электрического поля являются также электрически заряженные тела. Связь электрического поля с вызывающим его зарядом устанавливают постулат Максвелла и теорема Гаусса:

; .

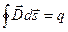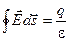Мы помним, что линии векторов электрического смещения и напряженности электрического поля начинаются на положительных и заканчиваются на отрицательных зарядах.

Линии индукции магнитного поля являются замкнутыми сами на себя (не имеют начала и конца), что математически выражается принципом непрерывности магнитного потока:

.

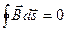Мы вспомнили основные уравнения электромагнитного поля в интегральной форме. С одной стороны в них находятся интегралы по поверхностям или по контурам от векторов поля, а с другой – суммы токов или зарядов в некоторой области пространства.

Из этих уравнений ничего нельзя сказать о величине векторов поля ( D, E, B,H) в отдельных точках пространства. При этом неясно, как влияет распределение токов или зарядов, записанных в правой части уравнений, на величины векторов в отдельных точках. А именно эта информация необходима для расчета локальных нагревов, усилий, запаса электрической прочности и других важных технических параметров электротехнических устройств и установок.

Мы использовали интегральные соотношения для введения интегральных параметров электрических цепей. Сопротивлениерезистора (R) характеризует связь между напряжением и током в устройстве, позволяет определить тепловые потери в нем, но не дает информации, как распределен ток внутри проводника. Электрическая емкость конденсатора (С) характеризует связь между зарядом и разностью потенциалов между двумя заряженными телами в диэлектрике, позволяет определить запасенную в нем энергию электрического поля, но не дает информацию о величинах напряженности в произвольных точках диэлектрика. Индуктивностькатушки (L) является коэффициентом пропорциональности между током в катушке и созданным им магнитным потоком, позволяет определить запасенную в ней энергию магнитного поля, однако не дает информацию о распределение магнитного поля около проводника с током и внутри него.

Вместе с тем имеются некоторые уравнения, дающие связь между различными характеристиками поля в каждой точке пространства:

; ;

; ; .

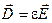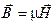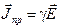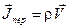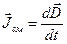Три последние составляющие плотности тока формально объединяют в одно уравнение:

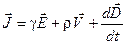
Следует иметь в виду, что первое и второе слагаемое в этом уравнении не могут существовать одновременно в одной и той же точке пространства.

Представим уравнения, записанные в интегральной форме, в так называемой дифференциальной форме, т.е. получим связь между физическими величинами, характеризующими поле, в каждой точке пространства.