Показатели формы распределения

Для получения приблизительного представления о форме распределения строят графики распределения (полигон и гистограмму). Однородные совокупности характеризуются, как правило, одновершинными распределениями. Многовершинность свидетельствует о неоднородности изучаемой совокупности. В этом случае необходима перегруппировка данных с целью выделения более однородных групп.

Выявление общего характера распределения предполагает оценку степени его однородности, а также исчисление показателей асимметрии и эксцесса.

Для сравнительного анализа степени асимметрии нескольких распределений рассчитывается относительный показатель асимметрии (А_S):

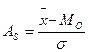. (5.27)

Если коэффициент асимметрии меньше 0,25, то асимметрия незначительная, если свыше 0,5, то асимметрия значительная.

Другой показатель асимметрии, предложенный шведским математиком Линдбергом, исчисляется по формуле:

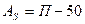, (5.28)

где П – процент тех значений признака, которые превышают величину средней арифметической;

50 – процент вариант, превосходящих среднюю арифметическую ряда нормального распределения.

Наиболее распространенным является показатель асимметрии, исчисляемый по формуле: 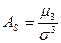, (5.29)

где m - центральный момент третьего порядка;

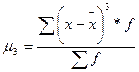. (5.30)

Этот показатель асимметрии не только определяет степень асимметрии, но и указывает на наличие или отсутствие асимметрии в распределении признака в генеральной совокупности. Оценка степени существенности этого показателя дается с помощью средней квадратической ошибки, рассчитываемой по формуле:

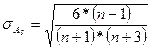, (5.31)

где n – число наблюдений.

Если 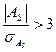, асимметрия существенна и распределение признака в генеральной совокупности не является симметричным.

Если 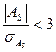, асимметрия несущественна, ее наличие объясняется наличием случайных обстоятельств.

Для симметричных распределений рассчитывается показатель эксцесса (островершинности): 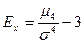, (5.32)

где 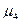- центральный момент четвертого порядка;

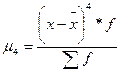. (5.33)

У высоковершинных распределений показатель эксцесса имеет положительный знак (+), а у низковершинных отрицательный знак (-). Предельным значением отрицательного эксцесса является значение 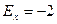; величина положительного эксцесса является величиной бесконечной. В нормальном распределении .

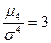Средняя квадратическая ошибка эксцесса исчисляется по формуле:

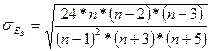, (5.34)

где n – число наблюдений.

Для приближенного определения величины эксцесса может быть использована формула Линдберга:

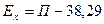, (5.35)

где П – процент количества вариант, лежащих в интервале, равном половине среднего квадратического отклонения (в ту и другую сторону от величины средней);

38,29 – процент количества вариант, лежащих в интервале, равном половине среднего квадратического отклонения, в общем количестве вариант ряда нормального распределения.