Структурный синтез технического объекта

Задача синтеза технического объекта включает в себя создание структуры проектируемого объекта и расчет его параметров. Эти две части синтеза соответственно называются структурным и параметрическим синтезом. Задача структурного синтеза заключается в поиске оптимальной или рациональной структуры (схемы) технического объекта для реализации заданных функций в рамках выбранного принципа действия.

Существо получения математических моделей объектов проектирования электронно-вычислительной и радиоэлектронной аппаратуры, для решения задач структурного синтеза, рассмотрим на примере компоновки, размещения, трассировки.

Задача компоновки

Под задачами компоновки понимают задачи разбиения множества D=(d₁,d₂,..., d_n) из п элементов на ряд непересекающихся подмножеств D_k, k=1,...,N, чтобы при этом выполнялись заданные ограничения и достигался экстремум некоторой функции качества F(x).

При заданном числе N подмножеств разбиения задача компоновки формулируется следующим образом:

F(x) → min (1)

и для любых k, l, принадлежащих множеству {l,2,..., N}выполняется:

D_k∩D_l=Ø; (2)

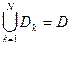(3)

где D_k - множество элементов, принадлежащих k-муподмножеству разбиения при условии, что мощность |D_k| каждого подмножества из разбиения задана, т.е.

|D_k| = n_k; ∑n_k =n (4)

Просмотреть все варианты разбиения уже для числа п>100нереально!

Применяя целочисленное программирование, можно уменьшить число просматриваемых вариантов компоновки.

Пусть требуется распределить п компонентов электронной схемы между N блоками таким образом, чтобы суммарное число связей между блоками было минимально.

Введем вектор X={x_i,k} переменных проектирования,

где x_i,k- элементы вектора X, i = 1,…,n; k = 1,…,N;

x_i,k =1, если компонент d_i включается в подмножествоD_k;

x_i,k =0 в противном случае.

Пусть функция качества F(x) характеризует общее число связей между подмножествами:

{D_k } для k = 1,N, тогда, задача компоновки запишется:

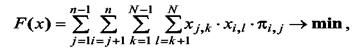(5)

при условиях:

(6)

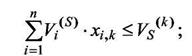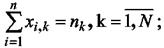(7)

(8)

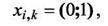(9)

где π_i,,j - число связей между компонентами di и dj,

V_i^(S) - значение параметра S для компонента d_i;

V_s^(k) - ограничение по параметру S, накладываемое на подмножество D_k;

S - любой параметр, подчиняющийся свойству аддитивности: объем; масса; энергоемкость, стоимость и т.п.

Условия 6 и 7 означают, что каждый компонент может быть отнесен только к одному из подмножеств D_k и в каждом подмножестве D_k может содержаться компонентов не более, чем заданное число n_k.

Задача размещения

Высокая плотность размещения элементов ЭВА создает большие трудности при реализации соединений между ними. В этой связи задача размещения элементов на плоскости определяет быстроту и качество трассировки. Оптимальное размещение элементов обеспечивает повышение надежности проектируемого устройства, минимизацию наводок, задержек сигналов, уменьшение общей длины соединений и т.п.

Формально задача размещения заключается в определении оптимального варианта расположения элементов на плоскости в соответствии с введенным критерием. Например, с минимальной взвешенной длиной соединений.

В общем случае требуется найти размещение компонентов d₁ ..., d_n на множестве q₁, q₂,…,q_m (m≤n) позиций монтажного пространства, при котором суммарная длина соединений между компонентами была бы минимальной. Введем булевы переменные:

x_i,k = 1, если компонент d_i назначается на позицию q_k;

x_i,k = 0 в противном случае.

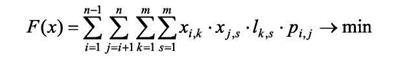Тогда математическая модель задачи размещения может быть записана:

(10)

при условиях:

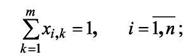(11)

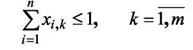(12)

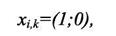(13)

где l_k,s- расстояние между позициями q_k и q_s; p_ij - число связей между компонентами d_i, d_j.

Задача трассировки

Задача трассировки встречается при конструировании печатных плат; разработке систем водоснабжения, электроснабжения и т.д.

Трассировка соединений является, как правило, заключительным этапом конструкторского проектирования ЭВА и состоит в определении линий, соединяющих эквипотенциальные контакты элементов и компонентов, составляющих проектируемое устройство.

Задача трассировки - одна из наиболее трудоемких в общей проблеме автоматизации проектирования ЭВА. С математической точки зрения трассировка - наисложнейшая задача выбора из огромного числа вариантов оптимального решения.

Основная задача трассировки формулируется следующим образом: по заданной схеме соединений проложить необходимые проводники на плоскости (плате, типовом элементе замены, кристалле и т.п.), чтобы реализовать заданные электрические соединения с учетом заранее заданных ограничений. Основными являются ограничения

На ширину проводников и минимальное расстояние между ними.

Исходной информацией для решения задачи трассировки соединений обычно являются список цепей, параметры конструкции элементов и коммутационного поля, а также данные по размещению элементов.

Критериями трассировки, наиболее часто используемые для оценки качества решения задачи трассировки, могут быть:

· процент реализованных соединений,

· суммарная длина проводников,

· число монтажных слоев,

· число межслойных переходов,

· минимальная область трассировки и др.

Задача трассировки всегда имеет топологический и метрический аспекты. Топологический аспект связан с выбором допустимого пространства расположения отдельных фрагментов соединений без фиксации их конкретного месторасположения при ограничениях на число пересечений и слоев. Метрический аспект предполагает учет конструктивных размеров элементов, соединений и коммутационного поля, а также метрических ограничений на трассировку.

Рассмотрим одну разновидность задачи трассировки - задачу построения связывающих сетей минимальной длины для цепей α_k.

Пусть U_k - множество точек, соединяемых по электрической цепи a_k;

|U_k| =n_k, где каждому элементу U_k соответствует одна точка в монтажном пространстве.

Введем понятие трассы.

Трасса - множество связанных отрезков, соединяющих точки электрической цепи.

Определим переменную проектирования x_ij

x_ij = 1, если ребро (i,j), длиной l включается в связывающую сеть;

x_ij =0, в противном случае,

где x_ij - булева переменная.

Тогда математическая модель задачи трассировки запишется:

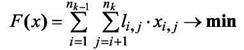(14)

при условиях:

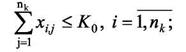(15)

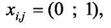(16)

где К₀ - максимально допустимое число соединений в одной точке.

Условие (15) означает, что в одной точке не могут соединяться количество ребер более заданного числа К_0.

Для контроля связности сети при решении задачи трассировки, математическая модель (17,18) может быть дополнена условиями:

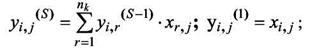(17)

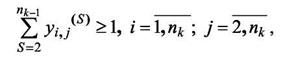(18)

где y_ij - вспомогательные переменные.

Суть ограничений (17,18) в том, что на каждом шаге принятия решения «включать - не включать ребро в трассу» должны рассматриваться точки соединений, принадлежащие одной цепи.