Термодинамический процесс
Изменение состояния термодинамической системы во времени называется термодинамическим процессом. Так, при перемещении поршня в цилиндре объём, а с ним давление и температура находящегося внутри газа будут изменяться, будет совершаться процесс расширения или сжатия газа.
Как уже отмечалось, система, выведенная из состояния равновесия, и предоставленная при постоянных параметрах окружающей среды самой себе, через некоторое время вновь придет в равновесное состояние, соответствующее этим параметрам. Такое самопроизвольное (без внешнего воздействия) возвращение системы в состояние равновесия
называется релаксацией, а промежуток времени, в течение которого система возвращается в состояние равновесия, называется временем релаксации. Для разных процессов он различно: если для установления равновесного давления в газе требуется всегда, то для выравнивания температуры в объеме того же газа нужны десяти; минут, а в объеме нагреваемого твердой тела — иногда несколько часов.
Термодинамический процесс называется равновесным, если все параметры системы при его протекании меняются достаточно медленно по сравнению с соответствующим процессом релаксации. В этом случае система фактически все время находится в состоянии равновесия с окружающей средой, чем и определяется название процесса.
Чтобы процесс был равновесным, скорость изменения параметров системы 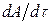 должна удовлетворять соотношению
должна удовлетворять соотношению
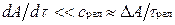
где А — параметр, наиболее быстро изменяющийся в рассматриваемом процессе; срел — скорость изменения этого параметра в релаксационном процессе; τрел — время релаксации.
Рассмотрим, например, процесс сжатия газа в цилиндре. Если время смещения поршня от одного положения до другого существенно превышает время релаксации, то в процессе перемещения поршня давление и температура успеют выровняться по всему объему цилиндра.
Это выравнивание обеспечивается непрерывным столкновением молекул, в результате чего подводимая от поршня к газу энергия достаточно быстро и равномерно распределяется между ними. Если последующие смещения поршня будут происходить аналогичным образом, то состояние системы в каждый момент времени будет практически равновесным. Таким образом, равновесный процесс состоит из непрерывного ряда последовательных состояний равновесия, поэтому в каждой его точке состояние термодинамической системы можно описать уравнением состояния данного рабочего тела. Именно поэтому классическая термодинамика в своих исследованиях оперирует только равновесными процессами. Они являются удобной идеализацией реальных процессов, позволяющей во многих случаях существенно упростить решение задачи. Такая идеализация вполне обоснована, так как условие (1.8) выполняется на практике достаточно часто. Поскольку механические возмущения распространяются в газах со скоростью звука, процесс сжатия газа и цилиндре будет равновесным, если скорость перемещения поршня много меньше скорости звука.
Процессы, не удовлетворяющие условию 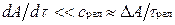 , протекают с нарушением равновесия, т. е. являются неравновесными. Если, например, быстро увеличит температуру окружающей среды, то газ в цилиндре будет постепенно прогреваться через его стенки, релаксируя к состоянию равновесия, соответствующему новым параметрам окружающей среды. В процессе релаксации газ не находится в равновесии с окружающей средой и его нельзя характеризовать уравнением состояния хотя бы потому, что в разных точках объема газа температура имеет различные значения.
, протекают с нарушением равновесия, т. е. являются неравновесными. Если, например, быстро увеличит температуру окружающей среды, то газ в цилиндре будет постепенно прогреваться через его стенки, релаксируя к состоянию равновесия, соответствующему новым параметрам окружающей среды. В процессе релаксации газ не находится в равновесии с окружающей средой и его нельзя характеризовать уравнением состояния хотя бы потому, что в разных точках объема газа температура имеет различные значения.
Теплоемкость газов
Отношение количества теплоты 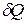 , полученного телом при бесконечно малом изменении его состояния, к связанному с этим изменению температуры тела
, полученного телом при бесконечно малом изменении его состояния, к связанному с этим изменению температуры тела 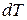 , называется теплоемкостью тела в данном процессе:
, называется теплоемкостью тела в данном процессе:
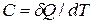 .
.
Обычно теплоемкость относят к единице количества вещества и в зависимости от выбранной единицы различают:
удельную массовую теплоемкость c , отнесенную к 1 кг газа,
Дж/(кг·К);
удельную объемную теплоемкость c´, отнесенную к количеству газа, содержащегося в 1 м3 объема при нормальных физических условиях, Дж/(м3·К);
удельную мольную теплоемкость 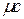 , отнесенную к одному киломолю, Дж/(кмоль·К).
, отнесенную к одному киломолю, Дж/(кмоль·К).
Зависимость между удельными теплоемкостями устанавливается очевидными соотношениями: 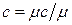 ;
; 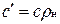
Здесь 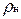 — плотность газа при нормальных условиях.
— плотность газа при нормальных условиях.
Изменение температуры тела при одном и том же количестве сообщаемой теплоты зависит от характера происходящего при этом процесса, поэтому теплоемкость является функцией процесса. Это означает, что одно и то же рабочее тело в зависимости от процесса требует для своего нагревания на 1 К различного количества теплоты. Численно величина с изменяется в пределах от +∞ до -∞.
В термодинамических расчетах большое значение имеют:
теплоемкость при постоянном давлении
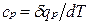 ,
,
равная отношению количества теплоты 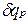 , сообщенной телу в процессе при постоянном давлении, к изменению температуры тела dT
, сообщенной телу в процессе при постоянном давлении, к изменению температуры тела dT
теплоемкость при постоянном объеме
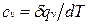 , (1.5)
, (1.5)
равная отношению количества теплоты , подведенной к телу в процессе при постоянном объеме, к изменению температуры тела .
В соответствии с первым законом термодинамики для закрытых систем, в которых протекают равновесные процессы 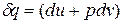 , и
, и
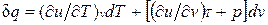 .
.
Для изохорного процесса (v=const) это уравнение принимает вид 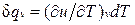 , и, учитывая (1.5), получаем, что
, и, учитывая (1.5), получаем, что
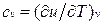 ,
,
т. е. теплоемкость тела при постоянном объеме равна частной производной от его внутренней энергии по температуре и характеризует темп роста внутренней энергии в изохорном процессе с увеличением температуры.
Для идеального газа 
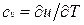
Для изобарного процесса () из уравнения (2.16) и (2.14) получаем
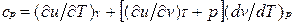
или
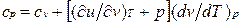
Это уравнение показывает связь между теплоемкостями ср и сv. Для идеального газа оно значительно упрощается. Действительно, внутренняя энергия идеального газа определяется только его температурой и не зависит от объема, поэтому 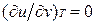 и, кроме того, из уравнения состояния следует
и, кроме того, из уравнения состояния следует 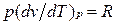 , откуда
, откуда
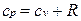 .
.
Это соотношение называется уравнением Майера и является одним из основных в технической термодинамике идеальных газов.
В процессе v=const теплота, сообщаемая газу, идет лишь на изменение его внутренней энергии, тогда как в процессе р = const теплота расходуется и на увеличение внутренней энергии и на совершение работы против внешних сил. Поэтому ср больше сv на величину этой работы.
Для реальных газов 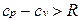 , поскольку при их расширении (при p=const) совершается работа не только против внешних сил, но и против сил притяжения, действующих между молекулами, что вызывает дополнительный расход теплоты.
, поскольку при их расширении (при p=const) совершается работа не только против внешних сил, но и против сил притяжения, действующих между молекулами, что вызывает дополнительный расход теплоты.
Обычно теплоемкости определяются экспериментально, но для многих веществ их можно рассчитать методами статистической физики.
Числовое значение теплоемкости идеального газа позволяет найти классическая теория теплоемкости, основанная на теореме о равномерном распределении энергии по степеням свободы молекул. Согласно этой теореме внутренняя энергия идеального газа прямо пропорциональна числу степеней свободы молекул и энергии kТ/2, приходящейся на одну степень свободы. Для 1 моля газа
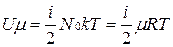 ,
,
где Nо — число Авогадро; i — число степеней свободы (число независимых координат, которые нужно задать для того, чтобы полностью определить положение молекулы в пространстве) .
Молекула одноатомного газа имеет три степени свободы соответственно трем составляющим в направлении координатных осей, на которые может быть разложено поступательное движение. Молекула двухатомного газа имеет пять степеней свободы, так как помимо поступательного движения она может вращаться около двух осей, перпендикулярных линии, соединяющей атомы (энергия вращения вокруг оси, соединяющей атомы, равна нулю, если атомы считать точками). Молекула трехатомного и вообще многоатомного газа имеет шесть степеней свободы: три поступательных и три вращательных.
Поскольку для идеального газа 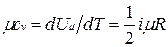 , то мольные теплоемкости одно-, двух- и многоатомных газов равны соответственно:
, то мольные теплоемкости одно-, двух- и многоатомных газов равны соответственно:
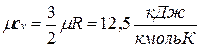 ;
; 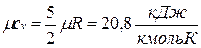 ;
; 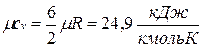 .
.
Результаты классической теории теплоемкости достаточно хорошо согласуются с экспериментальными данными в области комнатных температур (табл. 2.1), однако основной вывод о независимости от температуры эксперимент не подтверждает. Расхождения, особенно существенные в области низких и достаточно высоких температур, связаны с квантовым поведением молекул и находят объяснения в рамках квантовой теории теплоемкости.
Теплоемкость некоторых газов при t= 0°С в идеально-газовом состоянии
| Газ | Число степеней свободы | Мольная теплоемкость, кДж/кмольК | k = ср /сv |
| Гелий Не | 12,60 | 1,660 | |
| Аргон Аг | 12,48 | 1,660 | |
| Кислород 02 | 20,96 | 1,397 | |
| Водород Н2 | 20,30 | 1,410 | |
| Азот М2 | 20,80 | 1,400 | |
| Метан СН4 | 26,42 | 1,315 | |
| Аммиак ЫН3 | 26,67 | 1,313 | |
| Диоксид угле- рода СО2 | 27,55 | 1,302 |
Эта теория устанавливает, прежде всего, несправедливость теоремы о равномерном распределении энергии по степени свободы в области низких и высоких температур. С уменьшением температуры газа происходит «вымораживание» числа степеней свободы молекулы. Так, для двухатомной молекулы происходит «вымораживание» вращательных степеней свободы и она вместо пяти имеет три степени свободы, а следовательно, и меньшую внутреннюю энергию и теплоемкость. С увеличением температуры у многоатомных молекул происходит возбуждение внутренних степеней свободы за счет возникновения колебательного движения атомов молекулы (молекула становится осциллятором). Это приводит к увеличению внутренней энергии, а следовательно, и теплоемкости с ростом температуры.
Теплоемкость реального газа зависит от давления, правда, очень слабо.
Поскольку теплоемкость реального газа зависит от температуры, в термодинамике различают истинную и среднюю теплоемкости.
Средней теплоемкостью сср данного процесса в интервале температур от t1 до t2 называется отношение количества теплоты, сообщаемой газу, к разности конечной и начальной температур:
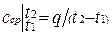
Выражение
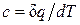 *
*
определяет теплоемкость при данной температуре или так называемую истинную теплоемкость. Из * следует, что
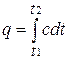
поэтому
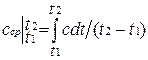 .
.
Для практических расчетов теплоемкости всех веществ сводят в таблицы, причем с целью сокращения объема таблиц средние теплоемкости приводят в них для интервала температур от 0 до t.
ЛЕКЦИЯ 2
Дата добавления: 2016-11-04; просмотров: 2077;











