Дифференциал функции
Для функции одной переменной 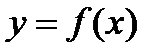 дифференциал функции определялся как главная, линейная относительно
дифференциал функции определялся как главная, линейная относительно 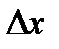 , часть приращения функции, равная произведению
, часть приращения функции, равная произведению 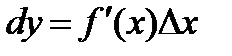 .
.
Обобщим данное определение для функции двух переменных.
Опр. Полным дифференциалом функции 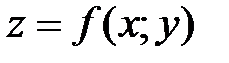 называется главная часть приращения функции, линейная относительно
называется главная часть приращения функции, линейная относительно 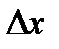 и
и 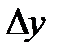 , т.е.
, т.е.
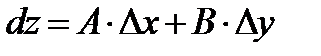 (1)
(1)
Выражения 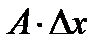 и
и 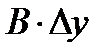 называют частными дифференциалами. Ранее было показано, что для независимых переменных х и у имеют место равенства
называют частными дифференциалами. Ранее было показано, что для независимых переменных х и у имеют место равенства 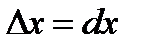 и
и 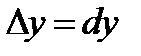 . Тогда равенство (1) примет вид
. Тогда равенство (1) примет вид 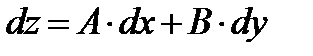 .
.
Рассмотрим без доказательства две теоремы.
Теорема1. Если функция 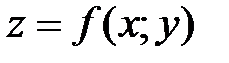 дифференцируема в точке
дифференцируема в точке 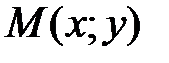 , то она непрерывна в этой точке, имеет в ней частные производные
, то она непрерывна в этой точке, имеет в ней частные производные 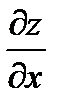 ,
, 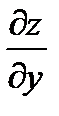 и выполняются равенства
и выполняются равенства 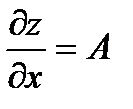 ,
, 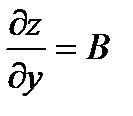 .
.
Теорема 2. Если функция 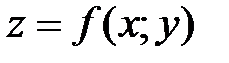 имеет непрерывные частные производные
имеет непрерывные частные производные 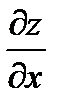 и
и 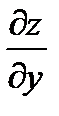 в точке
в точке 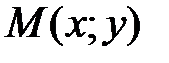 , то она дифференцируема в этой точке и ее полный дифференциал выражается формулой
, то она дифференцируема в этой точке и ее полный дифференциал выражается формулой
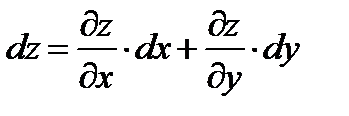 (2) или
(2) или 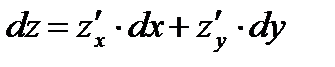 (3).
(3).
Арифметические свойства и правила нахождения дифференциалов функции одной переменной сохраняются и для дифференциалов функции двух (и большего числа) переменных.
Пример 1. Найти полный дифференциал функции 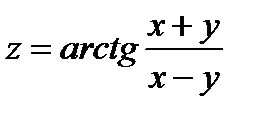 .
.
Решение.Найдем частные производные функции
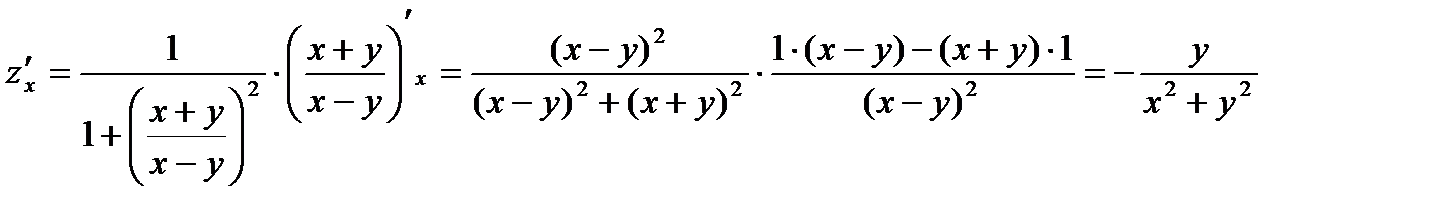 .
.
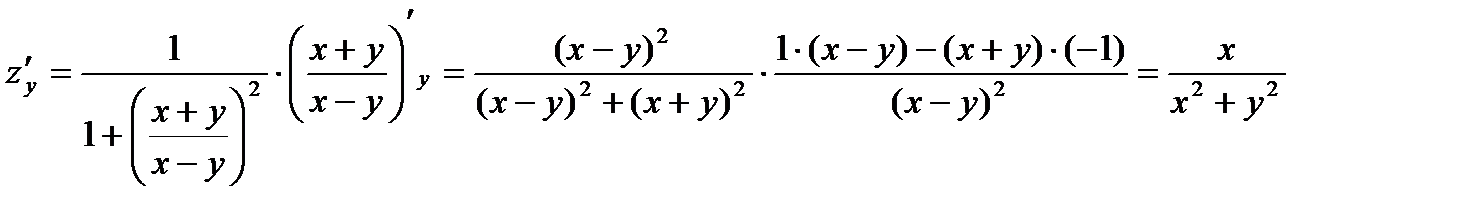 .
.
Применим формулу (3), получим:
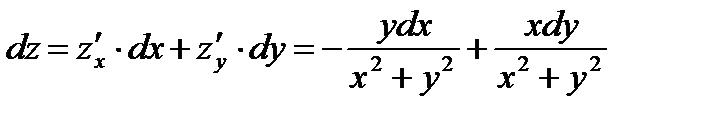 .
.
Полный дифференциал функции называют также дифференциалом первого порядка. Если функция 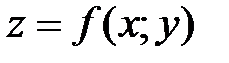 имеет непрерывные частные производные второго порядка, то можно найти дифференциал второго порядка, применив формулу
имеет непрерывные частные производные второго порядка, то можно найти дифференциал второго порядка, применив формулу
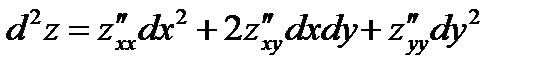 (4).
(4).
Дифференциалы, порядок которых выше первого, называют дифференциалами высших порядков.
Пример 2. Найти дифференциал второго порядка для функции 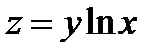 .
.
Решение. Найдем производные первого порядка
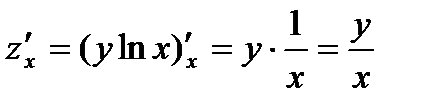 .
. 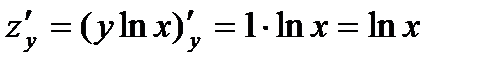 .
.
Найдем производные второго порядка
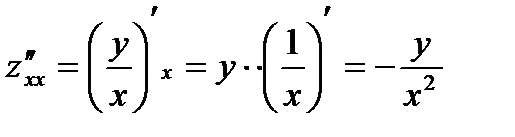 ,
, 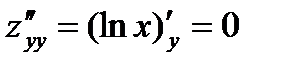 ,
, 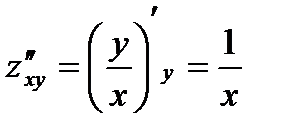 .
.
Применим формулу (4) 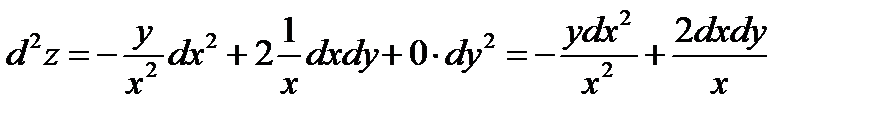
Дата добавления: 2021-02-19; просмотров: 166;










