Искажение расстояний
Небольшой участок сферической поверхности при определенных условиях можно принять за плоскость.
Применение модели плоской поверхности при решении геодезических задач возможно лишь для небольших участков поверхности Земли, когда искажения, вызванные заменой поверхности сферы или эллипсоида плоскостью невелики и могут быть вычислены по простым формулам. Это тем более оправдано, если учесть, что измерения на местности и чертежные работы всегда выполняются с ошибками, а потому небольшую часть сферы (эллипсоида), отличающуюся от плоскости на величину, меньшую ошибок измерений, можно считать плоской.
Рассчитаем, какое искажение получит дуга окружности, если заменить ее отрезком касательной к этой дуге. На рис.1.7 точка O - центр окружности, дуга ABC радиусом R стягивает центральный угол ε. Проведем касательную через середину дуги в точке B и, продолжив радиусы OA и OC до пересечения с касательной, получим точки A' и C'.
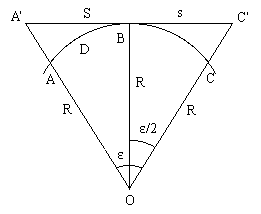
Рис.1.7
Пусть дуга ABC имеет длину D, а отрезок касательной A'C' - длину S. Известно, что для окружности D = R* ε, причем угол ε должен быть выражен в радианах.
Из ΔOBC' имеем:
S/2=R*tg(ε/2) или S = 2 R tg(ε/2) (1.1)
Разность (S - D) обозначим через ΔD и напишем
ΔD=R*[2*tg( ε/2)- ε] (1.2)
Разложим tg(ε/2) в ряд, ограничившись ввиду малости угла ε/2 двумя членами разложения,
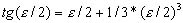 или
или 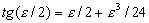 .
.
Подставим это выражение в формулу (1.2) и получим
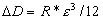 .
.
Но ε = D/R, поэтому
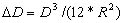 .
.
Отношение ΔD/D называется относительным искажением длины дуги при замене ее отрезком касательной, оно будет равно:
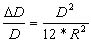 (1.3)
(1.3)
Подсчитаем конкретные значения относительного искажения для раз ных длин дуги D ( R = 6400 км): D = 20 км, Δ D/D = 1/1 218 000,
D = 30 км, Δ D/D = 1/ 541 000, и т.д.
Достигнутая точность измерения расстояний пока не превышает 1/1 000 000, поэтому при геодезических работах любой точности участок сферы 20 х 20 км2 можно считать плоским. При работах пониженной точности размеры участка сферы, принимаемого за плоскость, можно увеличить.
Дата добавления: 2021-02-19; просмотров: 561;











